7. Фотометрические величины и единицы. Сила света, освещенность, светимость, яркость.

В тетради

8. Волны. Общие свойства. Уравнение плоской монохроматической волны (тригонометрическая и комплексная формы представления).

Волны – физические возмущения, распределяются в среде (вакууме) и несущие с собой энергию.

Основные виды волн:

• Упругие (звуковые, волны в твердых телах)

• Волны на поверхности жидкости

• Электромагнитные (Радиоволны, световые)

По форме различают:

1. Одиночная волна или импульс.

ξ – некое возмущение

Короткие возмущения не имеющие регулярного характера.

Ограниченный ряд повторяющихся возмущений, называют цугом волн.

Цуг волны

2. Гармоническая волна (Идеализация)

По виду волн различают поперечные и продольные.

В поперечной волне физическая величина совершает колебания в направлениях перпендикулярных распространению волны.

В продольной волне направление колебания физической величины и направление распространения совпадают.

Геометрическое место точек до которых доходят колебания к некоторому моменту времени называется волновым фронтом. (может быть только один)

Геометрическое место точек колеблющихся в одинаковых фазах называется волновой поверхностью, (может быть много).

Волновая поверхность может быть любой, но есть 2 случая:

1. Плоские волны

2. Сферические волны

Одномерный случай когда волна распространяется строго по оси х.

1. Период (Т) – время совершения одного полного колебания

2. – частота

3. – длина волны – расстояние пройденное волной за 1 период

Уравнение плоской и сферической волн.

а) Плоская волна

(1);

А – амплитуда;

Для текущего момента времени

(2)

Условия постоянства фазы:

Продифференцируем

– фазовая скорость волны

Следовательно, скорость распространения волны описываемой уравнением (2), есть скорость перемещения фазы волны.

Введем понятия волнового числа.

(3) – волновое число

(3а)

(4)

– определяет периодичность процесса во времени

k – периодичность процесса в пространстве

С учетом затухания для волны пишем

(5)

б) Уравнение сферической волны

Для полной фазы

Амплитуда сферической волны уменьшается обратно пропорционально расстоянию.

(6)

9. Электромагнитная теория света. Уравнения Максвелла для вакуума. Скорость света.

Существование электромагнитных волн было предсказано Максвеллом как прчмое следствие из его уравнений.

Электромагнитные волны (ЭМВ) – является поперечной волной.

Свет является поперечной волной

По Максвеллу свет является ЭМВ очень высоких частот.

Уравнение Максвелла для световой волны.

­­­– _­­­­напряженность электрического поля.

– напряженность магнитного поля

– свободные заряды отсутствуют

j=0 – нет тока проводимости

(1)

(2)

Рассмотрим второе уравнение системы (1):

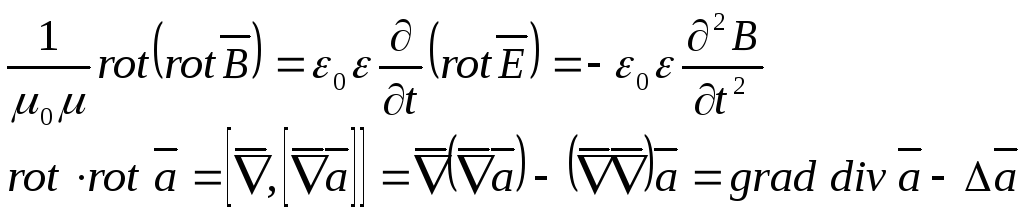
(3)

(4)

Вывод: Два взаимосвязанных уравнения (3) и (4) определяют процесс распространения световой волны в среде с параметрами

(волновое уравнение)

(5)

Оптика: среда не магнитная, т.е. , поэтому (6)

Вакуум:

(7)

(7) с учетом (6):

В обычной среде: (8)

С другой стороны (9)

Из (8), (9) следует (10) , где n – определяет оптические свойства среды, – определяет электрические свойства среды

(1а)

Имеем решение этой системы в виде плоских гармонических волн.

(11)

Вывести:

Прав.часть І =

(12)

Выводы:

1. Из ІІІ и ІV уравнения системы (12), что

2. Из І и ІІ уравнений системы (12) следует, что векторы и взаимно ортогональны и образуют правую тройку векторов.

3. Т.к. коэффициенты в І и ІІ системы (12) действительные величины, то и достигают своих максимальных и минимальных значений в одни и те же моменты времени.

4. Найдем связь между векторами и . Для этого обратимся к первому уравнению системы (12) и найдем модуль:

(13)

H – напряженность магнитного поля

(14)

(15)

5. Плотность потока световой энергии

– вектор Умова-Пойнтинга

(16)

(17)

Физический смысл (16) (16а)

[]=

|S| – определяет плотность потока энергии световой волны, т.е. количество энергии переносимой световой волной в единицу времени, через единичную площадку, расположенной перпендикулярно направления распространения света.

6. Интенсивность света

(18) – интенсивность световой волны

Выводы:

Свет, как электромагнитная волна, характеризуется следующими параметрами:

1. Длина волны:

Для вакуума (видимый диапазон световых волн)

;

2. Оптическая среда

n – показатель преломления среды

3. Световая волна переносит с собой энергию с плотностью потока . При оптических измерениях регистрируется интенсивность света величиной

4. Световая волна является поперечной волной и характеризуется поляризацией

а) Естественный свет

б) Линейно-поляризованный свет

10. Поперечность световых волн. Связь между Ē и .

11. Плоская световая волна и её характеристики. Поток и плотность потока энергии. Вектор Пойнтинга. Интенсивность света.

12. Нормальное падение света на границу раздела двух сред. Коэффициенты отражения и пропускания световой волны.

13. Сложение колебаний. Интенсивность результирующего колебания. Когерентность и некогерентность. Интерференция.

Написано на листочке

14. Интерференция световых волн. Интерференционная картина.

Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света.

Рис. 3.7.1 - Наблюдение колец Ньютона. Интерференция возникает при сложении волн, отразившихся от двух сторон воздушной прослойки. «Лучи» 1 и 2 – направления распространения волн; h – толщина воздушного зазора

Первый эксперимент по наблюдению интерференции света в лабораторных условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны (рис. 3.7.1).

Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона (рис. 3.7.2).

Рис. 3.7.2

Ньютон не смог с точки зрения корпускулярной теории объяснить, почему возникают кольца, однако он понимал, что это связано с какой-то периодичностью световых процессов.