Раздел III. Игровые модели принятия решения

В этом разделе показано применение принципа оптимального поведения (принципа минимакса) при вычислении оптимальных чистых стратегий, способ доминирования чистых стратегий, а также общий метод нахождения оптимальных смешанных стратегий в матричных играх (сведение матричной игры к двойственным задачам линейного программирования).

Литература: [12-15]

§1. Основные сведения из теории матричных игр.

Любую конфликтную ситуацию принятия решения, в которой участвуют две стороны (игрока) с противоположными интересами и с конечным числом возможностей (стратегий), можно описать в виде матрицы

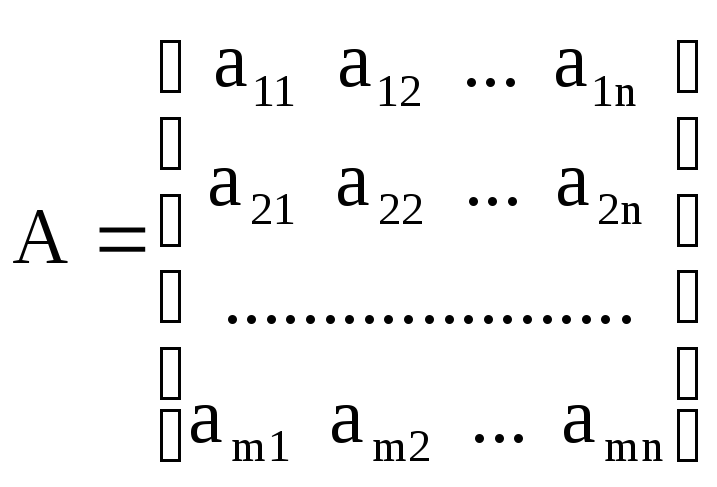(1)

В этой модели выбор Iигрока сводится к выбору строки (mчистых стратегий), выбор IIигрока -к выбору столбца (nчистых стратегий); а_ij - выигрыш Iигрока при стратегиях (i,j); выигрыш IIигрока при тех же стратегиях есть число а_ijс противоположным знаком (игра антагонистическая). Каждый игрок выбирает свою стратегию так, чтобы получить как можно больший выигрыш.

В отличие от ранее рассмотренных задач оптимизации в модели (1) участвуют два ЛПР. Наша задача заключается в вычислении "оптимальных" стратегий и соответствующих им выигрышей обоих ЛПР (игроков).

Стратегия i* (j*) называется оптимальной чистой стратегией первого (второго) игрока, если для любых i =1,2,...,mиj=1,2...nвыполнено неравенство

a_ij*≤a_i*j*≤a_i*j (2)

Пара оптимальных стратегий (i*j*) называется седловой точкой, а числоa_i*j* -значением (или ценой) игры (1).

Свойства матричных игр.

1.Седловая точка в матричных играх существует не всегда (примеры см. в[14]).Она существует тогда и только тогда, когда

(3)

Поэтому принципы оптимальности в матричных играх называются принципом минимакса (или максимина).

2.Значение игры, если оно существует, является наименьшим числом в своей строчке и наибольшим в своем столбике.

3.Оптимальные стратегии не изменятся, если ко всем элементам матрицы(1)прибавить или отнять одно и то же число или умножить все элементы матрицы на одно и то же положительное число.

4.Игра (1)может иметь несколько седловых точек. Если (i*,j*), () - седловые точки, то (i*,) и (,j*) - тоже седловые точки (взаимозаменяемость) иa_i*j*===(эквивалентность).

5.Если игра (1) не имеет оптимальных чистых стратегий, то вводят смешанные стратегии:

x=(x₁,…,x_m): 0≤x_i≤1,i=1,…,m;x₁+…+x_n=1 и

=(y₁,…,y_n): 0≤y_j≤1,j=1,…,n;y₁+…+y_n=1;

х -смешанная стратегия 1игрока; у -смешанная стратегия IIигрока. Таких стратегий у игроков бесконечное множество.

6.В любой матричной игре существуют оптимальные смешанные стратегииx*,y*:

(4)

для любых стратегий х, у. Значением игры в смешанных стратегиях называется число

Решить игру (1)это значит найти пару оптимальных стратегий (чистых или смешанных) и значение игры.

§ 2. Решение игры в чистых стратегиях.

Пример 1.Найти оптимальные чистые стратегии и значения следующей матричной игры:

Чтобы упростить эту игру, умножим каждый элемент матрицы А на 12,а затем каждому элементу прибавим 6(чтобы избавиться от отрицательных чисел) - см. свойство 3:

Сравнивая элементы первой строки (выигрыши, соответствующие первой чистой стратегии Iигрока) с соответствующими элементами четвертой строки видим, что Iигрок однозначно предпочтет первую стратегию, т.е. четвертую стратегию использовать не будет. Поэтому ее можно исключить из рассмотрения:

В этом случае говорят, что первая стратегия доминирует четвертую стратегию.

Так как IIигрок (выбирающий столбики) минимизирует выигрыш Iигрока, то, как видно из последней матрицы, вторая стратегия IIигрока доминирует его первую и третью стратегии, а пятая -четвертую. В итоге исключения доминируемых стратегий получим игру

Игра А' эквивалентна исходной игре в том смысле, что в них оптимальные стратегии одинаковы (свойство 3),aν(A') =12ν(A)+6

В игре А' применяем принцип минимакса (3).Вычислим левую часть равенства (З):

max{6,1,3}=6.

Вычислим правую часть равенства (З):

min{l0,7} =7.

Так как равенство (3)не выполнено, то в игре А' и, значит, в игре А, оптимальных чистых стратегий нет.

Пример 2.Решить игру

Решение:max{-2,1,3,-6)=3,

min{3,6,5)=3.

Оптимальные стратегии: i*=3(третья строка),j*=1(первый столбик); значение игрыν(А)=3.

Пример 3.Решить игру

В этой игре четыре седловые точки: (1,2), (1,4),(2,1), (2,4);значение игрыν(А)=3. Алгоритм решения матричной игры в чистых стратегиях следующий;

1)выполнить доминирование стратегий для обоих игроков;

2)вычислить обе части равенства (3);если равенство выполнено, то игра имеет решение в чистых стратегиях; если не выполнено -то оптимальных чистых стратегий нет.