§3. Решение задачи лп симплекс-методом.

Пример 5.(Решение Задачи ЛП данной в канонической форме):

min f(x)=x₁+9x₂ + 5x₃ + 3x₄+4x₅+14x₆ (4)

при ограничениях

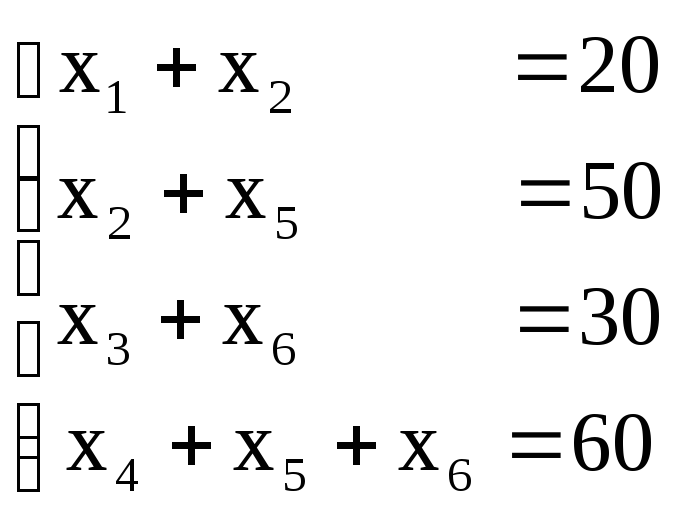(5)

x_i≥0,i=1,…,6.

Говорят, что задача ЛП имеет каноническую форму, если все ограничения (кроме условий неотрицательности переменных) имеют вид строгих равенств, а все свободные члены неотрицательны.

Идея симплекс-метода заключается в следующем. Сначала надо найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем надо проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Ввиду конечности вершин многогранника (следствие конечности числа ограничений задачи ЛП) за конечное число "шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).

Таким образом, идея симплекс-метода основывается на трех свойствах задачи ЛП (см. §1).

Решение.Чтобы найти начальное допустимое базисное решение (н.д.б.р.), т.е. чтобы определить базисные переменные, систему (5)нужно привести к "диагональному виду". Применяя метод Гаусса (метод последовательного исключения неизвестных), получаем из (5):

(7)

Следовательно, базисными являются переменные x₂,x₄,x₅,x₆, им придаем значения, равные свободным членам соответствующих строк:x₂=40,x₄=20,x₅=10,x₆=30. Переменныеx₁иx₃являются небазиснымиx₁=0,x₃=0.

Построим н.д.б.р.

x⁰=(0, 40, 0, 20, 10, 30) (8)

Для проверки на оптимальность найденного решения x⁰нужно из целевой функции исключить базисные переменные (с помощью системы (7))и построить специальную таблицу (таково требование симплекс-метода).

После исключения переменных целевую функцию удобно написать в виде:

f(x)+7x₁-14x₃=880 (9)

Теперь при помощи (7),(8),(9) составляем начальную симплекс-таблицу:

Таблица 1

		x1	x2	x3	x4	x5	x6	- шапка таблицы
f	880	7	0	14	0	0	0	- нулевая строка
x2	40	1	1	1	0	0	0
x4	20	1	0	0	1	0	0	…
x5	10	-1	0	-1	0	1	0
x6	30	0	0	1	0	0	1	- четвертая строка

первый столбик … шестой столбик

нулевой столбик

базисный столбик

В нулевую строчку записаны коэффициенты соответствующих переменных при целевой функции. Так как все переменные в (4),неотрицательны, то целевая функция тем меньше, чем меньше эти коэффициенты. Отсюда критерий оптимальности: д.б.р. (х⁰) оптимально, если в нулевой строчке нет ни одного строго положительного числа (не считая значения целевой функции (880)). Это правило отражается и на следующие итерации (таблицы). Элементы нулевой строки будем называть оценками столбцов.

Так, что н.д.б.р. (8) неоптимально: 7>0, 14>0.

В нулевом столбике записаны значения базисных переменных. Они обязательно должны быть неотрицательными (см. условие (6)).От первой по четвертую строки написаны коэффициенты переменных из системы (7).

Так как x⁰неоптимально, то надо перейти к другой вершине многогранника допустимых решений (построить новое д.б.р.). Для этого нужно найти ведущий элемент и провести симплексное преобразование (таково требование симплекс-метода).

Ведущий элемент таблицы стоит в пересечении ведущего столбика (столбец с наибольшей положительной оценкой) и ведущей строки (строки, соответствующей минимальному соотношению элементов нулевого столбика к соответствующим элементам (строго положительным) ведущего столбика.

В таблице 1ведущий столбик -третий столбик, и ведущая строка -четвертая строка(min {40/1,30/1}=30/1)обозначены стрелками, а ведущий элемент — кружочком. Ведущий элемент показывает, что базисную переменнуюx₆нужно заменить на небазиснуюx₃. Тогда новыми базисными переменными будутx₂,x₃,x₄,x₅, а небазисными –x₁,x₆. Это и означает переход к новой вершине х⁰⁰ многогранника допустимых решений. Чтобы найти значения координат д.б.р. х⁰⁰, нужно строить новую симплекс-таблицу и провести в ней элементарные преобразования:

а) все элементы ведущей строки поделить на ведущий элемент, превратив этим самым ведущий элемент в 1(для простоты выкладок);

б) с помощью ведущего элемента (равного 1)все элементы ведущего столбика превратить в нули (аналогично методу исключения неизвестных);

В результате в нулевом столбце получены значения новых базисных переменных x₂,x₃,x₄,x₅(см. таблицу 2)- базисные компоненты новой вершины х⁰⁰ (небазисные компонентыx₁=0,x₆=0).

Таблица 2

		x1	x2	x3	x4	x5	x6
f	460	7	0	0	0	0	-14
x2	10	(1)	1	0	0	0	-1
x4	20	1	0	0	1	0	0
x5	40	-1	0	0	0	1	1
x3	30	0	0	1	0	0	1

Как показывает таблица 2новое базисное решение x⁰⁰=(0,10, 30, 20, 40, 0) неоптимально (в нулевой строке есть неотрицательная оценка 7),Поэтому с ведущим элементом 1(см. таблицу 2)строим новую симплекс-таблицу, т.е. строим новое д.б.р. (таблица З):

Таблица 3

		x1	x2	x3	x4	x5	x6
f	390	0	-7	0	0	0	-7
x1	10	1	1	0	0	0	.1
x4	10	0	-1	0	1	0	1
x5	50	0	1	0	0	1	0
x3	30	0	0	1	0	0	1

Таблице 3соответствует д.б.р.

x⁰⁰⁰= (10, 0 ,30. 10, 50,0),

и оно оптимально, т.к. внулевойстрочке нет положительных оценок. Поэтому

f(x⁰⁰⁰) = 390

есть минимальное значение целевой функции.

Ответ: х⁰⁰⁰ =(10, 0, 30, 10, 50,О) -точка минимума

f(x⁰⁰⁰) = 390

Пример 6.(Решение задачи ЛП,не имеющей каноническую форму):

minf(x) =x₁ –x₂ –x₃ (8)

при ограничениях

(9)

x₁,x₂,x₃≥0 (10)

Умножая обе части (9)на -1и прибавляя в левые части системы дополнительные (или слабые) переменныеx₄≥0, x₅≥0,x₆≥0,получаем, каноническую форму (слабые переменные на целевую функцию не влияют):

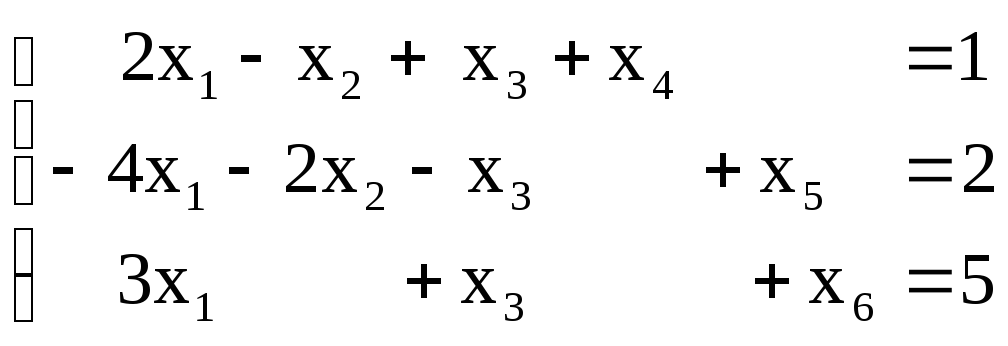(11)

x₁,…,x₆≥0

Так как все слабые переменные входят со знаком "+'',то их можно взять в качестве базисных и составить н.д.б.р. х⁰=(0, 0, 0, 1, 2, 5).В данном случае исключать базисные переменные из целевой функции нет надобности (т, к. они в ней отсутствуют), поэтому целевую функцию записываем сразу в виде

f(x)-x₁+x₂+3x₃=0 (12)

(требование симплекс-метода). С помощью н.д.б.р. х⁰и выражений (11) и (12) составим начальную симплекс-таблицу (здесьf(x⁰)=0).

		x1	x2	x3	x4	x5	x6
f	0	-1	1	3	0	0	0
x4	1	2	-1	(1)	1	0	0
x5	2	-4	2	-1	0	1	0
x6	5	3	0	1	0	0	1

Так как x⁰неоптимален (в нулевой строке есть положительные числа 1и 3), то с обозначенным ведущим элементом строим новое д.б.р. И так далее. На четвертой итерация (шаге) получаем таблицу:

		x1	x2	x3	x4	x5	x6
f	-46/3	0	0	0	-19/3	-11/3	-1/3
x3	4	0	0	1	2	1	е
x2	11/3	0	1	0	-1/3	1/3	2/3
x1	1/3	1	0	0	-1/2	-1/3	1/3

В качестве упражнения проверьте правильность вычисления элементов этой таблицы, выполнив пропущенные две итерации (таблицы).

Как видно из последней таблицы, оптимальным решением задачи является

x⁰⁰⁰⁰=(l/3,1l/3,4) и f(x⁰⁰⁰⁰)=-46/3

Как итог рассмотрения двух примеров, приведем алгоритм симплекс-метода:

1) Привести задачу к канонической форме;

2) Привести систему ограничений к диагональной форме и определить базисные переменные;

3) исключить базисные переменные из целевой функции;

4) достроить симплекс-таблицу;

5) проверить найденное д.б.р. на оптимальность: если оно оптимально, то решение закончить; если нет, то идти к пункту 6;

6) вычислить ведущий элемент таблицы;

7) провести симплексное преобразование;

8) Построить новое д.б.р. и идти к пункту 5

П р и м е ч а н и як симплекс-методу.

1.Если в ведущем столбике нет ни одного строго положительного элемента, то задача не имеет оптимального решения, а целевая функция неограничена снизу (в задаче на минимум) или неограничена сверху (в задаче на максимум).

2.Несовместимость системы ограничений (в канонической форме) обнаруживается при построении начального д.б.р. (оно не существует).

3.Если в последней (оптимальной) таблице оценка какой-либо небазисной переменной (число в нулевой строке) равна нулю, то задача, имеет бесконечное множество оптимальных решений.

4.Симплекс-метод за конечное число итераций либо приводит к оптимальному решению, либо устанавливает неразрешимость задачи (см. пп.1.2,3).

5.На каждой итерации симплекс-метод сохраняет допустимость базисного решения, т.е. неотрицательность элементов нулевого столбика -следствие правила выбора ведущей строки.

6. На каждой итерации целевая функция убывает (в задаче на минимум) или возрастает (в задаче на максимум); это свойство нарушается только в случае зацикливания (см. примечания 11,12).

7.В качестве ведущего столбика можно выбирать любой столбик с положительной оценкой (в задаче на минимум), однако, максимальность оценки ведущего столбика ведет к сокращению числа итераций (целевая функция быстро убывает).

8. Слабые переменные со знаком "+" (вводимые для канонизации неравенств вида “≤”) можно использовать в качестве базисных переменных, и слабые переменные со знаком “-” (вводимые для канонизации неравенств вида “≥”) - нет.

9. Структуру симплекс-таблицы можно упростить, если на каждой итерации исключать из таблицы столбики для базисных переменных. При этом сокращается объем вычислений.

10. При решении симплекс-методом задачи на максимум изменяется только правило выбора ведущей строки (столбик с минимальной отрицательной оценкой) и критерий оптимальности (отсутствие в нулевой строке отрицательных оценок).

11. Д.б.р., в котором одна или несколько базисных переменных равны нулю, называется вырожденным д.б.р. Появление такого д.б.р. в процессе решения может привести к зацикливанию, т.е. к повторному вхождению переменной в базис (геометрически: возвращение к предыдущей вершине многогранника). Предвестником зацикливания является, неоднозначное определение ведущей строки.

12. Для выхода из зацикливания: в критерии определения ведущей строки вместо элементов 0-го столбика применяют элементы 1-го столбика; если и здесь ведущая строка неоднозначна, то применяют элементы 2-го столбика и так далее, пока ведущая строка не будет определена однозначно.