
Crack_Mат_прогр_1_Посiбн
.pdfНовий опорний розв’язок такий: X (2) = (0;12; 4; 0;1) . |
За розв’язний |
||||||||
вибираємо четвертий стовпець, в ньому розв’язний елемент |
визначаємо з |
||||||||
умови min |
12 |
; |
4 |
|
|
|
=12. За розв’язний елемент виберемо 1 на перетині |
||
|
|
|
|
|
|
||||
1/3 |
|
||||||||
|
1 |
|
|
|
|
|
|
||
4-го стовпця і 2-го рядка. В результаті перетворень дістанемо:
БН |
|
x1 |
x2 |
x |
|
x4 |
|
x5 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
|
|
|
|
|
|
x3 |
|
2/3 |
1/3 |
0 |
|
0 |
|
1 |
|
5 |
x4 |
|
1 |
1 |
0 |
|
1 |
|
0 |
|
12 |
x5 |
|
1/3 |
-1/3 |
1 |
|
0 |
|
0 |
|
0 |
x5 |
|
2/3 |
1/3 |
0 |
|
0 |
|
1 |
|
4 |
x4 |
|
0 |
1 |
-2 |
|
0 |
|
1 |
|
5 |
x1 |
|
0 |
2 |
-3 |
|
1 |
|
0 |
|
12 |
x1 |
|
1 |
-1 |
3 |
|
0 |
|
0 |
|
0 |
|
X (3) =(0;12;4;0;1). Аналогічно знаходимо |
X (4) |
=(0;0;0;12;5) |
і |
||||||
X (5) |
= (0;0;0;12;5). |
|
|
|
|
|
|
|
|
|
|
Отже, ми знайшли п’ять опорних розв’язків. |
|
|
|
|
|
||||
3 Геометричний метод розв’язування задач лінійного програмування
3.1 Загальна і основні задачі лінійного програмування
Означення 1. Загальною задачею лінійного програмування називається задача, яка полягає у визначенні максимального (мінімального) значення функції
F = ∑n |
cj xj |
|
|
|
|
|
|
(1) |
|
|
j=1 |
|
|
|
|
|
|
|
|
при обмеженнях |
|
||||||||
∑n |
aij xj ≤bi |
(i = |
|
|
), |
|
(2) |
||
1,k |
|||||||||
j=1 |
|
|
|
|
|
|
|
|
|
∑n |
aij xj =bi |
(i = |
|
), |
(3) |
||||
k +1,m |
|||||||||
j=1 |
|
|
|
|
|
|
|
|
|
xj |
≥0 |
( j = |
|
, l ≤ n), |
(4) |
||||
1,l |
|||||||||
де aij , bi , cj − задані постійні величини і k ≤ m.
20
Означення 2. Функція (1) називається цільовою функцією (або лінійною формою) задачі (1) - (4), а умови (2) - (4) - обмеженнями даної задачі.
Означення 3. Стандартною (або симетричною) задачею лінійного програмування називається задача, яка полягає у визначенні максимального значення функції (1) при виконанні умов (2) і (4), де k = m і l = n .
Означення 4. Канонічною (або основною) задачею лінійного програмування називається задача, яка полягає у визначенні максимального значення функції (1) при виконанні умов (3) і (4), де k =0 і l = n.
Означення 5. Сукупність чисел X =(x1 , x2 ,..., xn ) , що задовольняють
обмеження задачі (2) - (4), називається допустимим розв’язком (або планом).
Означення 6. План X * =(x1* , x2* ,..., xn* ) , при якому цільова функція
(1) приймає своє максимальне значення, називається оптимальним. Значення цільової функції (1) при плані X будемо позначати через
F(X ). Відповідно, якщо X * − оптимальний план задачі, то для будь-якого X виконується нерівність F(X ) ≤ F(X * ) .
Щоб перейти від одної форми запису задачі лінійного програмування до іншої, потрібно в загальному випадку, по-перше, зводити задачу мінімізації функції до задачі максимізації, по-друге, переходити від обмежень-нерівностей до обмежень-рівностей і навпаки, по-третє, замінювати змінні, які не задовольняють умову невід’ємності.
В тому випадку, |
коли |
потрібно |
знайти мінімум функції |
F =c1 x1 + c2 x2 +... + cn xn , можна |
перейти до |
знаходження максимуму |
|
функції F1 = −F = −c1 x1 − c2 x2 |
−... − cn xn , оскільки min F = −max(−F ) . |
||
Обмеження нерівності вихідної задачі лінійного програмування вигляду “ ≤”, можна перетворити в обмеження-рівності шляхом додавання до їх лівих частин додаткових невід’ємних невідомих, а обмеженнянерівності вигляду “ ≥” - в обмеження-рівності відніманням від їх лівих частин додаткових невід’ємних невідомих. Таким чином, обмеженнянерівність
ai1 x1 + ai2 x2 +... + ain xn ≤bi
перетворюється в обмеження-рівність
ai1 x1 + ai2 x2 |
+... + ain xn + xn+1 =bi (xn+1 ≥0), |
(5) |
а обмеження-нерівність |
|
|
ai1 x1 + ai2 x2 |
+... + ain xn ≥bi |
|
в обмеження-рівність
ai1 x1 |
+ ai2 x2 |
+... + ain xn − xn+1 =bi (xn+1 ≥0), |
(6) |
В той же час кожне рівняння системи обмежень |
|
||
ai1 x1 |
+ ai2 x2 |
+... + ain xn =bi |
|
21
можна записати у вигляді нерівностей: |
|
|||||
a x + a |
x |
+... + a |
x |
≤b |
, |
(7) |
i1 1 i2 |
2 |
in |
n |
i |
|
|
−ai1 x1 − ai2 x2 −... − ain xn ≤ −bi . |
|
|||||
3.2 Геометричний спосіб розв’язування задач лінійного програмування
Означення 7. Множина називається опуклою, якщо разом з довільними двома точками вона містить і їх довільну опуклу комбінацію.
Означення 8. Точка X опуклої множини називається кутовою, якщо вона не може бути представлена у вигляді опуклої лінійної комбінації будь-яких двох інших різних точок даної множини.
Теорема 1. Множина планів основної задачі лінійного програмування є опуклою (якщо вона непорожня).
Означення 9. Непорожня множина планів основної задачі лінійного програмування називається многокутником розв’язків, а довільна кутова точка многокутника розв’язків – вершиною.
Теорема 2. Якщо основна задача лінійного програмування має оптимальний план, то максимальне значення цільова функція задачі прийме в одній із вершин многокутника розв’язків. Якщо максимальне значення цільова функція задачі приймає більше ніж в одній вершині, то вона приймає його в довільній точці, яка є опуклою лінійною комбінацією цих вершин.
Нехай дано задачу лінійного програмування:
F =c1 x1 + c2 x2 →max |
(8) |
||||||
при обмеженнях: |
|
||||||
a |
x + a |
x |
≤b |
|
|
||
11 |
1 |
12 |
2 |
|
1 |
|
|
a21 x1 + a22 x2 ≤b2 |
|
(9) |
|||||
............................ |
|||||||
|
|
|
|
|
|
|
|
a |
x |
+ a |
x |
|
≤b |
|
|
m1 1 |
m2 2 |
|
m |
|
|||
дляx1 ≥0, |
x2 ≥0 |
|
|
|
|
(10) |
|
в яку входять тільки дві змінні: x1 і x2 .
Кожна з нерівностей системи обмежень (9) і (10) визначає на координатній площині x1Ox2 деяку півплощину. При цьому, якщо
x ≤ − |
ai1 |
x + |
bi |
, то це нижня півплощина, а якщо |
x ≥ − |
ai1 |
x + |
bi |
- то |
|
|
|
|
||||||
2 |
ai2 |
1 |
ai2 |
|
2 |
ai2 |
1 |
ai2 |
|
|
|
|
|
|
|
верхня. Отже, областю допустимих розв’язків – множиною D задачі (8) – (10) є перетин (спільна частина) скінченної кількості півплощин, тобто деяка багатокутна область на площині.
22
Графічний метод розв’язання задач лінійного програмування застосовується в основному в задачах з обмеженнями у вигляді системи нерівностей, які містять дві змінні.
Розв’язання таких задач виконується в два етапи:
перший етап – побудова області допустимих розв’язків – множини D; другий етап – пошук в цій області оптимального розв’язку.
Для побудови області допустимих розв’язків потрібно:
1)записати рівняння граничних прямих і побудувати їх графіки;
2)виділити області розв’язків кожної з нерівностей системи обмежень (9) і (10);
3)виділити область допустимих розв’язків D.
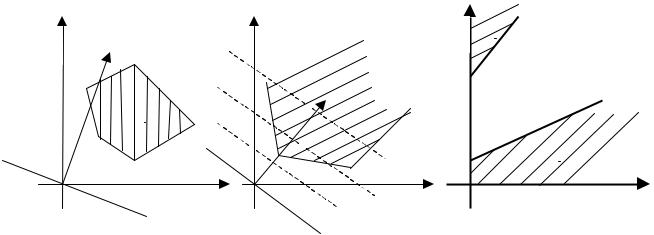
Зауваження 1. При побудові областей допустимих розв’язків D може мати місце один із трьох варіантів: 1) опуклий многокутник;
2)необмежена опукла багатокутна область; 3) пуста множина.
Впершому випадку задача не має розв’язку через те, що система обмежень несумісна в області допустимих розв’язків; в другому випадку задача завжди має оптимальний розв’язок; в третьому випадку задача може
мати або не мати розв’язку. Останнє пов’язано з необмеженим
зростанням ( F max→∞) або спаданням ( F min→-∞) функції F в області допустимих значень.
Х2 |
C |
Х2 |
|
|
|
Х2 |
Д |
|
|
|
|
|
|||
|
B |
|
A2 |
|
|
|
|
|
Д |
|
|
Д |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
B2 |
|
|
|
|
F |
|
|
|
|
|
|
|
A |
|
|
A |
B |
|
Д |
|
E |
|
|
|
|
||
0 |
0 |
|
|
0 |
|
||
Х1 |
|
|
Х1 |
Х1 |
|||
|
а) |
|
|
|
б) |
|
в) |
Рисунок 1 − Можливі варіанти допустимих розв’язків D
Далі необхідно перейти до другого етапу – знаходження оптимального розв’язку. Рівняння F =c1 x1 + c2 x2 при фіксованому значенні
F визначає пряму, а при зміні F − сім’ю паралельних прямих з
23
|
|
uuv |
|
параметром F . Вектор N ={c1 ,c2 }, перпендикулярний до всіх цих прямих, |
|||
вказує напрямок зростання параметра F . Для всіх точок, |
які лежать на |
||
одній з прямих, функція F приймає певне значення, тому вказані прямі |
|||
звуться лініями рівня для функції F . |
|
||
|
Для знаходження оптимального розв’язку потрібно: |
|
|
uuv |
1) |
на рисунку, де побудована область D , побудувати вектор |
|
N |
={c1 ,c2 } і лінію рівняння c1 x1 + c2 x2 = 0 ; |
|
|
|
2)uur шляхом паралельного переміщення лінії рівня у напрямку |
||
вектора N знайти спільну точку лінії рівня і області D . Це буде вершина |
|||
області D |
з координатами (x1 , x2 ). При подальшому |
паралельному |
|
переміщенні лінії рівня вона вже не буде мати спільних точок з областю
D ; |
|
знайти координати (x1 , x2 ) вершини області D , як перетин двох |
||||
|
3) |
|||||
прямих, які проходять через цю вершину; |
|
|
|
|||
|
4) |
обчислити |
максимальне |
значення |
цільової |
функції |
F |
= c x* + c x* . |
|
|
|
|
|
max |
1 |
1 2 2 |
|
|
|
|
|
Зауваження 2. |
Якщо лінійна |
функція |
F досягає |
свого |
|
екстремального значення в одній кутовій точці, що є вершиною багатокутної області, то задача має єдиний оптимальний розв’язок, якщо більше, ніж в одній точці, то задача має нескінченну кількість оптимальних розв’язків.
Зауваження 3. Для задачі мінімізації лінію рівня c1 x1 + c2 x2 = 0
необхідно паралельно переміщувати в напрямку, протилежному напрямку |
|
uur |
|
вектора N. |
|
Зауваження 4. Якщо при паралельному переміщенні лінія рівня |
|
весь час буде |
перетинати допустиму область D , то лінійна функція |
F =c1 x1 + c2 x2 |
необмежена зверху на допустимій множині і задача (8) – |
(10) немає оптимального розв’язку (рис. 1б).
Зауваження 5. Графічний спосіб розв’язування задач ЛП застосовується інколи у випадку якщо система обмежень задачі має більше, ніж дві змінні.
Приклад 1. Розв’язати графічно задачу лінійного програмування:
F = 2x1 +5x2 →max, при обмеженнях: |
|
||||
3x |
+ 9x |
≤18, |
, для |
x1 ≥0, x2 ≥0. |
|
|
1 |
2 |
|
||
3x1 |
+ 4x2 ≤12, |
|
|
||
Розв’язання.
Будуємо область допустимих розв’язків – множину D . Процес побудови спочатку подамо у динаміці.
24
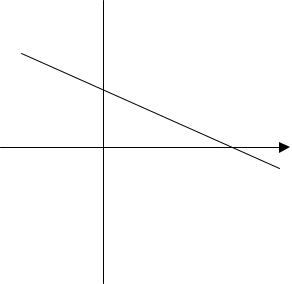
Розглянемо 1-шу нерівність 3x1 +9x2 ≤18 . Запишемо рівняння граничної прямої l1 : 3x1 +9x2 =18, оскільки рівняння з двома змінними в
двовимірному просторі, тобто на площині, геометрично зображає пряму лінію. В системі координат на площині побудуємо пряму. Для побудови прямої l1 досить взяти дві точки, які належать цій прямій. Візьмемо точки
перетину прямої з осями координат:
якщо x1 = 0, то x2 = 2 , якщо x2 = 0 , то x1 =6. Через точки (0, 2) і (6, 0) проводимо пряму l1 (рис. 2). Пряма l1 дану площину поділяє на дві півплощини. Нерівність 3x1 +9x2 =18 x2 ≤ −1/ 3x2 +3 визначає нижню півплощину по відношенню до прямої l1 . На рис. 2, ця півплощина заштрихована.
 X2
X2
l1
2
6 X1
0
Рисунок 2 – Розв’язки нерівності 1
Аналогічно 2-га нерівність: 3x1 + 4x2 ≤12 визначає граничну прямуl2 : 3x1 + 4x2 =12 . Для її побудови візьмемо точки перетину з осями координат: якщо x1 = 0, то x2 = 3, якщо x2 = 0 , то x1 = 4 . Через точки (0, 3) і (4, 0) проводимо пряму l2 (рис.3). Аналогічно як і для прямої l1 визначаємо напрямок штриховки та зображаємо її на рисунку. Нерівність x1 ≥0
геометрично зображає праву півплощину відносно осі ординат Ox2 , разом з граничною прямою x1 = 0 , яка збігається з віссю Ox2 . Аналогічно нерівність x2 ≥0 геометрично зображає верхню півплощину відносно осі
25
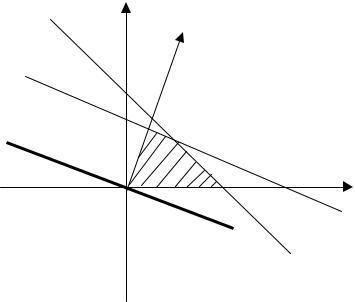
Ox1 |
разом з граничною прямою x2 |
= 0 , |
яка збігається з віссю Ox1 . Перетин |
|||
(спільна частина) цих чотирьох півплощин визначає допустиму область D . |
||||||
|
|
l2 |
X2 |
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
l1 |
|
3 |
n |
|
|
|
|
|
|
|
|
|
|
l |
А |
2 |
В |
|
|
|
|
|
|
|||
|
|
0 |
|
С |
6 |
X1 |
|
|
|
4 |
|
|
|
|
Рисунок 3 – Область допустимих розв’язків |
|
|
|||
Отже, допустимою областю D є опуклий многокутник ОАBC, який
на рис.3 заштрихований. Для того, щоб знайти оптимальний розв’язок uur
задачі лінійного програмування, будуємо вектор N ={2; 5}, який показує
напрям зростання функції F = 2x1 +5x2 . Лініями рівня є прямі 2x1 +5x2 |
= c , |
|||||
де c R. Надамо c |
значення нуля і проведемо пряму l : |
2x1 +5x2 |
= 0 , яка |
|||
проходить через |
початок координат, |
перпендикулярно |
до |
вектора |
||
uur |
|
|
|
|
|
|
N ={2; 5}(рис. 3). |
|
|
|
|
|
|
Щоб знайти найбільше значення функції |
F = 2x1 +5x2 |
на |
||||
многокутнику ОАBC, спочатку знаходимо точку, в якій це значення |
||||||
досягається. |
|
|
|
|
|
|
Для цього умовно переміщуємо прямуuurl : 2x1 +5x2 = 0 |
паралельно |
|||||
самій собі по області D в напрямку вектора N ={2; 5} |
до тих пір, поки |
|||||
вона не перестане перетинати область D . |
Найбільшого значення лінійна |
|||||
функція F = 2x1 +5x2 досягатиме у вершині В многокутника ОАBC, тобто у точці виходу прямої l з даної області.
Знайдемо координати точки В ( x1* ; x2* ). Точка В лежить на перетині прямих l1 і l2 . Для знаходження координат точки В необхідно розв’язати систему рівнянь:
26
|
3x |
+ 9x |
=18, |
|
|
|
|
|
|
|
|||
|
|
1 |
2 |
=12. |
|
|
|
|
|
|
|
||
|
3x1 + 4x2 |
|
|
|
|
|
|
|
|||||
|
Віднявши від першого рівняння системи друге, отримаємо: |
||||||||||||
|
5x |
=6 → x* |
= 6 . Тоді 3x |
=12 − 4x |
=12 − 4 6 |
= 36 , а відповідно |
|||||||
|
|
2 |
|
|
2 |
5 |
|
|
1 |
2 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|||
x* = 36 |
=12 |
. Тобто точка В має координати (12 ; 6 ). |
|
||||||||||
1 |
15 |
|
5 |
|
|
|
|
|
|
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
Отже, найбільше значення лінійної функції: |
|
|||||||||||
|
F = f (B) = 2 12 + 5 6 = 54 . |
|
|
|
|||||||||
|
|
max |
|
|
|
5 |
|
5 |
|
5 |
|
|
|
|
Приклад |
2. |
|
|
|
|
|
||||||
|
Знайти |
|
найбільше та |
найменше |
значення функції |
||||||||
F = 2x1 −3x2 |
при обмеженнях: |
|
|
|
|
|
|||||||
|
|
|
|
|
|
3x |
+ 2x |
≤12, |
|
|
|
||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
3x1 −5x2 ≤15, |
|
|
|
||||
|
|
|
|
|
|
x |
− x |
≥ −2, |
|
|
|
||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2x |
+ x |
≥ −6. |
|
|
|
||
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
Розв’язання:
Для знаходження області допустимих розв’язків множини D побудуємо граничні прямі:
1)l1 : 3x1 + 2x2 =12 , яка проходить через точки (0;6) та (4;0);
2)l2 : 3x1 −5x2 =15 , яка проходить через точки (0;-3) та (5;0);
3)l3 : x1 − x2 = −2 , яка проходить через точки (0; 2) та (-2;0);
4)l4 : 2x1 + x2 = −6 , яка проходить через точки (0;-6) та (-3;0).
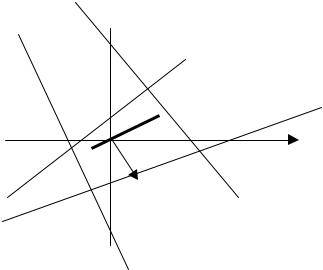
Врахувавши, що обмеженнями є система нерівностей, визначимо частини півплощин, що задовольняють їх розв’язок та знайдемо спільну область допустимих розв’язків – область D (рис.4).
l1  X2 l4 6
X2 l4 6
Вl3
|
2 |
|
|
l2 |
|
-3 -2 |
l |
4 |
5 |
X1 |
|
0 |
|||||
А |
|
С |
|||
|
|
||||
К |
-3 n |
|
|
|
|
|
-6 |
|
|
|
Рисунок 4 – Область допустимих розв’язків
27
|
Отже, допустимою областю D є опуклий многокутник АBCК, який |
|||||||||||||||||||
на рис.4 |
|
заштрихований. |
Для того, щоб знайти оптимальний розв’язок |
|||||||||||||||||
задачі лінійного програмування, знайдемо вектор |
uur |
|
|
|
|
|
|
|||||||||||||
N ={2; −3}. Проведемо |
||||||||||||||||||||
пряму |
l : |
|
2x1 −5x2 |
= 0 , |
яка |
|
проходить |
через |
початок |
|
|
координат, |
||||||||
|
|
|
|
|
|
|
uur |
(рис. 4). |
|
|
|
|
|
|
|
|
|
|||
перпендикулярно до вектора N |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Умовно переміщуємо пряму l : |
2x −5x |
= 0 |
паралельно самій собі |
||||||||||||||||
по області |
D у напрямі вектора |
uur |
1 |
2 |
до тих пір, поки вона не |
|||||||||||||||
N |
={2; −3} |
|||||||||||||||||||
перестане перетинати область |
D . Найбільшого значення лінійна функція |
|||||||||||||||||||
F = 2x1 −3x2 |
досягатиме в найбільш віддаленій вершині К многокутника |
|||||||||||||||||||
АBCК, тобто у точці виходу прямої |
з даної області. Знайдемо координати |
|||||||||||||||||||
точки |
К |
|
( x* ; x* ). Точка |
К лежить на перетині |
прямих |
l |
4 |
і |
l |
2 |
. Для |
|||||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
знаходження координат точки К необхідно розв’язати систему рівнянь: |
||||||||||||||||||||
|
3x |
−5x =15, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x1 + x2 = −6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Домножимо 2-ге рівняння системи на 5 і додамо до 1-го, |
|||||||||||||||||||
отримаємо: |
|
|
= −15 |
|
|
|
|
|
= −6 − 2 (−15) = −48 |
|
|
|
||||||||
13x |
|
= −15 → x* |
. Тоді x |
= −6 − 2x |
|
.Тобто |
||||||||||||||
|
2 |
|
|
2 |
13 |
|
|
2 |
|
1 |
|
|
13 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
48 ;− |
15 ). |
|
|
|
|
|
|
|
|
|
||||
точка К має координати ( − |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
13 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
Отже, найбільше значення лінійної функції: |
|
|
|
|
|
|
|
||||||||||||
|
F = F(K ) = 2 (−48) −3 (−15) = −51 . |
|
|
|
|
|
|
|
|
|||||||||||
|
|
max |
|
|
13 |
|
|
13 |
13 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Найменшого значення лінійна функція |
F = 2x1 −3x2 |
досягатиме в |
|||||||||||||||||
найближчій |
|
вершині В многокутника АBCК, тобто у точці входу прямої l |
||||||||||||||||||
у дану область. Знайдемо координати точки В ( x' |
; x' |
). Точка В лежить на |
|||||||
перетині прямих l1 |
і l3 . |
|
|
|
1 |
2 |
|
||
Для знаходження координат точки В необхідно |
|||||||||
розв’язати систему рівнянь: |
|
|
|
|
|
||||
3x + 2x =12, |
|
|
|
|
|
|
|||
|
1 |
2 |
|
|
|
|
|
|
|
x1 |
− x2 = −2. |
|
|
|
|
|
|
||
Домножимо 2-ге рівняння системи на 2 і додамо до 1-го, |
|||||||||
отримаємо: |
|
= 8 . Тоді x' |
= 2 + x = 2 + 8 |
=18 |
|
||||
5x |
=8 → x' |
.Тобто точка В має |
|||||||
1 |
|
1 |
5 |
2 |
1 |
5 |
5 |
|
|
|
|
|
|
|
|
||||
координати ( 8 |
;18 ). |
|
|
|
|
|
|
||
|
5 |
5 |
|
|
|
|
|
|
|
Отже, найменше значення лінійної функції: |
|
|
|||||||
F = F(B) = 2 8 |
−3 18 = −38 . |
|
|
|
|
||||
min |
|
5 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
28
4 Симплекс метод розв’язування задач лінійного програмування
4.1 Поняття про симплексний метод (симплекс метод)
Розглянемо канонічну задачу лінійного програмування, у якій система лінійних рівнянь розв’язана відносно одиничного базису і всі вільні члени невід’ємні числа:
F = −c0 + c1x1 + c2 x2 + c3 x3 + c4 x4 + c5 x5 + c6 x6 →max
x1 |
|
+ a14 x4 + a15 x5 + a16 x6 =b1 , |
|
|
|
|||||||
|
x |
+ a x |
+ a |
25 |
x |
+ a x ==b |
, |
|
|
|||
|
2 |
|
24 |
4 |
5 |
26 |
6 |
2 |
|
|
(1) |
|
|
x3 |
+ a34 x4 + a35 x5 |
+ a36 x6 ==b3 , |
|
||||||||
|
|
|
||||||||||
xj |
≥( j =1,2,...,6) |
|
|
|
|
|
|
|
|
|||
Запишемо цільову функцію у вигляді: |
|
|
||||||||||
F −c1 x1 −c2 x2 |
−c3 x3 −c4 x4 −c5 x5 |
− c6 x6 = −c0 |
|
(2) |
||||||||
Система (1) має опорний розв’язок |
X0 ={b1;b2 ;b3 ;0;0;0}при якому |
|||||||||||
F0 = −c0 +b1 x1 +b2 x2 + b3 x3 . |
|
|
|
1 |
|
( 2 ) |
|
2 |
||||
Рівняння |
( 1 ) |
помножимо на |
|
помножимо на |
||||||||
1 |
c |
, рівняння 1 |
c , |
|||||||||
рівняння (13 )помножимо на c3 |
і додамо до рівняння (2). Одержимо: |
|
||||||||||
F −c1 x1 − c2 x2 − c3 x3 − c4 x4 − c5 x5 − c6 x6 + c1 x1 + c1 (a14 x4 + a15 x5 + a16 x6 ) + c2 x2 + +c2 (a24 x4 + a25 x5 + a26 x6 ) + c3 x3 + c3 (a34 x4 + a35 x5 + a36 x6 ) = −c0 + c1b1 + c2b2 +
+c3b3
F + x4 (c1a14 + c2a24 + c3a34 − c4 ) + x5 (c1a15 + c2a25 + c3a35 − c5 ) + x6 (c1a16 +
+c2 a26 + c3a36 − c6 ) = F0 |
(3) |
|
Коефіцієнти цього рівняння |
|
|
a0k = ∑3 |
ci aik − ck , (k = 4,5,6) |
(4) |
i=1 |
|
|
Приєднаємо рівняння (3) до системи (1), вважаючи F |
базисною |
|
змінною. Складемо таблицю:
29
