Міністерство освіти і науки України

Вінницький національний технічний університет

Кафедра ТГП

Контрольна робота

з дисципліни «Математичні методи розв’язування інженерних задач»

Виконав: ст. гр. БТ-13

Гашинський Є.М.

Перевірила: Ободянська О.І.

Вінниця 2015

Завдання 1. Графічний метод: задача з нелінійною цільовою функцією й нелінійною системою обмежень.

Розв’язання:

Графічний метод можна використовувати для вирішення задачі НЛП, яка містить дві змінні х1 і х2, наприклад завдання такого вигляду: Z = f(x1, x2) → min (max); gi(x1, x2) ≤ bi, . Щоб знайти її оптимальне рішення, потрібно виконати наступні дії: 1. Знайти ОДЗ, яка визначається обмеженнями завдання. Якщо виявиться, що ця область порожня, то це означає, що задача не має рішення. 2. Побудувати сімейство ліній рівня цільової функції f (х1, х2) = C  при різних значеннях числового параметра С. 3. При виконанні завдання на мінімум визначити напрямок зменшення, а для задачі на максимум - напрям зростання ліній рівня ЦФ. 4. Знайти точку ОДЗ, через яку проходить лінія рівня з найменшим в задачі на мінімум (відповідно, найбільшим в завдання на максимум) значенням параметра С. Ця точка буде оптимальним рішенням. Якщо ЦФ не обмежена знизу в задачі на мінімум (зверху - в задачі на максимум), то це означає, що задача не має оптимального рішення. 5. Знайти координати точки оптимуму і визначити в ній значення ЦФ. Відзначимо, що на відміну від завдання ЛП точка оптимуму в задачі НП не обов'язково знаходиться на границі ОДЗ. Нею також може бути внутрішня точка цієї множини.

Завдання 2. Суть гетероскедастичності. Гетероскедастичність і зважений метод найменших квадратів.

У зв’язку із одним з припущень використання методу найменших квадратів необхідна наявність гомоскедастичності дисперсії залишків. Це означає, що для кожного фактору хі залишки еі мають однакову дисперсію. Якщо ця умова застосування МНК не дотримується, то спостерігається гетероскедастичність (див. рис. 4.1). Рис. 4.1. Приклади гетероскедастичності: 1 – дисперсія залишків досягає максимальної величини при середніх значеннях змінної х та зменшується при мінімальних та максимальних значеннях х; 2 – максимальна дисперсія залишків при малих значеннях х і дисперсія залишків однорідні по мірі зростання значень х. Гомоскедастичність залишків означає, що дисперсія залишків еі однакова для кожного значення х. Використовуючи тривимірне зображення покажемо гомо- і гетероскедастичність. Рис. 4.2. показує, що для кожного значення хі розподіли залишків еі однакові на відміну від розподілів на рис. 4.3, де діапазон варійованих залишків змінюється з переходом від одного значення хі до іншого. Останнє явище і носить назву гетероскедастичності.

Завдання 3. Побудувати на площині множину розв’язків (багатокутник) системи лінійних обмежень-нерівностей й геометрично знайти найбільше та найменше значення лінійної функції в цьому багатокутнику (x₁0, x₂0).

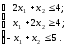
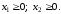
Розв’язання:

Задана економіко-математична модель є моделлю задачі лінійного програмування, що містить лише дві змінні, і тому може бути розв’язана графічно.

Перший крок згідно з графічним методом полягає в геометричному зображенні допустимих планів задачі, тобто у визначенні такої області, де водночас виконуються всі обмеження моделі. Замінимо знаки нерівностей на знаки строгих рівностей і побудуємо графіки відповідних прямих (рис.1).

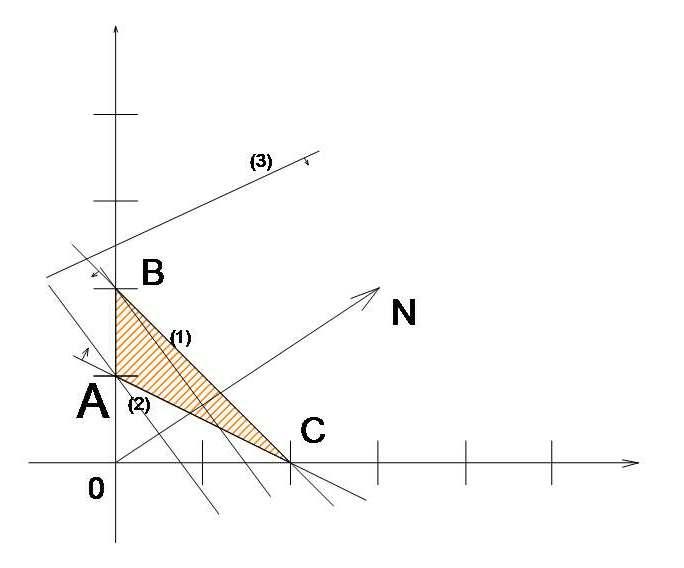
Рисунок 1

Кожна з побудованих прямих поділяє площину системи координат на дві півплощини. Координати точок однієї з півплощин задовольняють розглядувану нерівність, а іншої — ні. Щоб визначити необхідну півплощину (на рис.1 її напрям позначено стрілкою), потрібно взяти будь-яку точку і перевірити, чи задовольняють її координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності. Інакше таким зображенням є інша півплощина.

Умова невід’ємності змінних х₁ ≥ 0, х₂ ≥ 0 обмежує область допустимих планів задачі першим квадрантом системи координат. Переріз усіх півплощин визначає область допустимих планів задачі — чотирикутник OABC. Координати будь-якої його точки задовольняють систему обмежень задачі та умову невід’єм­ності змінних. Тому поставлену задачу буде розв’язано, якщо ми зможемо відшукати таку точку багатокутника OABC, в якій цільова функція Z набирає найбільшого та найменшого значення.

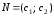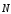Для цього побудуємо вектор , координатами якого є коефіцієнти при змінних у цільовій функції задачі. Вектор завжди виходить із початку координат і напрямлений до точки з координатами (х₁ = с₁; х₂ = с₂). У нашій задачі вектор 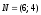. Він задає напрям збільшення значень цільової функції Z, а вектор, протилежний йому, — напрям їх зменшення.

Побудуємо лінію, що відповідає, наприклад, значенню Z=0. Це буде пряма 6х₁ + 4х₂ + 20 = 0, яка перпендикулярна до вектора 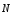. Оскільки в даному прикладі необхідно визначити найбільше значення цільової функції, то пересуватимемо пряму 6х₁ + 4х₂ + 20 = 0 паралельно самій собі згідно з напрямом вектора 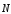доти, доки не визначимо вершину багатокутника, яка відповідає оптимальному плану задачі.

Із рис.1 видно, що останньою спільною точкою прямої цільової функції та багатокутника OABC є точка B. Координати цієї точки є оптимальним планом задачі.

Координати точки B є розв’язком системи рівнянь

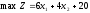
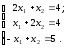
звідси маємо: х₁ = 3,6; х₂ = 6,6.

Отже,

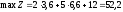
Виходячи з аналогічних міркувань, знаходимо, що ,

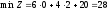х₁ = 0; х₂ = 2.

Завдання 4. Симплексним методом знайти розв’язок задачі, математична модель якої має вигляд:

z = 10х₁ +12х₂ +30 (max)

;

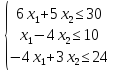
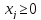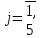
Розв’язання:

Розв’яжемо задачу симплекс-методом згідно з розглянутим алгоритмом.

I. Запишемо систему обмежень задачі в канонічному вигляді. Для цього перейдемо від обмежень-нерівностей до строгих рівнянь, увівши до лівої частини обмежень додаткові змінні х3, х4 та х5:

;

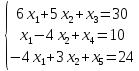
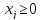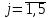
У цільовій функції Z додаткові змінні мають коефіцієнти, які дорівнюють нулю:

min z = 10х₁ + 12х₂ + 0х₃ + 0х₄ + 0х₅ +30

Канонічну систему обмежень задачі запишемо у векторній формі:

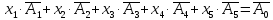
де

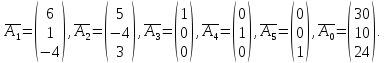
Оскільки вектори 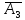, та 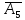одиничні та лінійно незалежні, то саме з них складається початковий базис у зазначеній системі век­торів. Змінні задачі х₃, x₄ та х₅, що відповідають одиничним базисним векторам, називають базисними, а решту — вільними змінними задачі лінійного програмування. Прирівнюючи вільні змінні до нуля, з кожного обмеження задачі дістаємо значення базисних змінних:

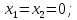
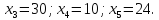
Згідно з визначеними 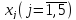векторна форма запису системи обмежень цієї задачі матиме вигляд:

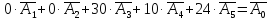
Оскільки додатні коефіцієнти х₃, х₄ та х₅ відповідають лінійно незалежним векторам, то за означенням

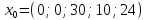
є опорним планом задачі і для цього початкового плану