2.2. Додавання взаємно перпендикулярних коливань

Розглянемо додавання двох гармонічних коливань однакової частоти ω, які відбуваються у взаємно перпендикулярних напрямках уздовж осей x і y. Для простоти початок відліку виберемо так, щоб початкова фаза першого коливання дорівнювала нулю:

(2.10)

де φ — різниця фаз обох коливань, А и В — амплітуди цих коливань.

Рівняння траєкторії результуючого коливання знаходиться шляхом виключення з рівнянь (2.10) часу t. Записавши коливання (2.10) у вигляді

і

і замінивши в другому рівнянні на і на одержимо після нескладних перетворень рівняння еліпса, осі якого орієнтовані відносно координатних осей довільно:

(2.11)

Так як траєкторія результуючого коливання має форму еліпса, то такі коливання називаються еліптично поляризованими. Орієнтація осей еліпса і його розміри залежать від амплітуд коливань (2.10) і різниці фаз φ.

Проведемо аналізу рівняння (2.11):

_{1. Нехай де} У даному випадку еліпс вироджується у відрізок прямої, рівняння якої має вигляд

(2.12)

де знак плюс відповідає нулю і парним значенням т (рис.8, а), а знак мінус — непарним значенням т (рис. 8,б).

Результуюче коливання є гармонічним коливанням з частотою ω і амплітудою ,якевідбувається уздовж прямої (2.12)і яке складає з віссю Ох кут У даному випадку коливання є лінійно поляризованими.

2. Нехай і.У даному випадку рівняння (2.11) прийме такий вигляд

(2.13)

Це рівняння еліпса, осі якого збігаються з осями координат, а його півосі дорівнюють відповідним амплітудам (рис. 9). Крім того, якщо А = В, то еліпс (2.13) вироджується у коло. Такі коливання називаються циркулярно поляризованими або коливаннями, які мають колову поляризацію.

Якщо частоти взаємно перпендикулярних коливань будуть різні, то замкнута траєкторія результуючого коливання буде мати досить складну форму. Замкнуті траєкторії, які утворюються при накладанні двох взаємно перпендикулярних коливань з кратними циклічними частотами, називаються фігурами Лиссажу. Форма цих кривих залежить від співвідношення амплітуд, частот і різниці фаз окремих коливань.

На рис. 10 показані фігури Лиссажу для різних співвідношень частот і різної різниці фаз.

Аналіз фігур Лиссажу — широко використовуваний метод дослідження співвідношень частот і різниці фаз коливань, що складаються, а також форми коливань. Тому вони знаходять широке застосування у вимірювальній техніці.

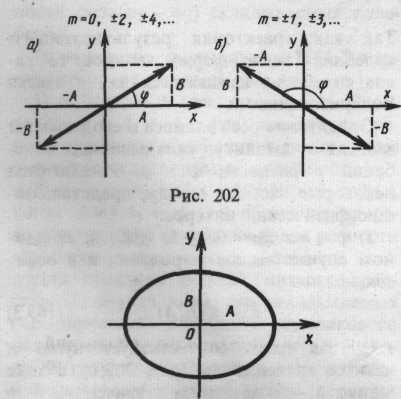
Рис. 9

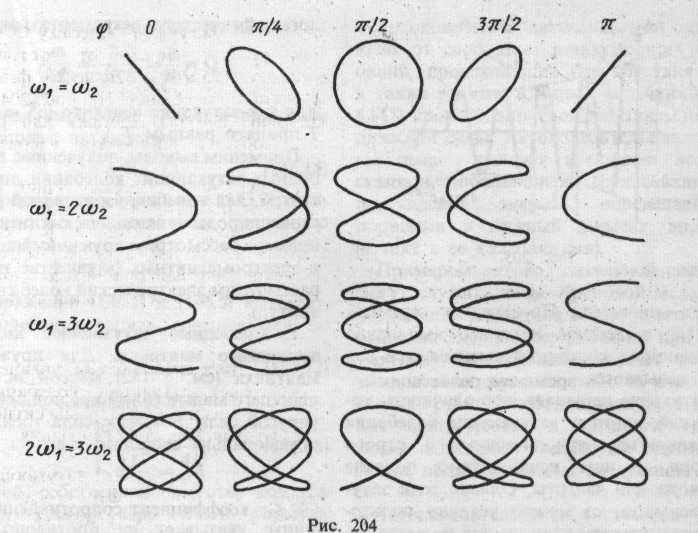
Рис.10

2.3. Диференціальне рівняння вільних затухаючих коливань і його розв’язування. Автоколивання

Розглянемо вільні затухаючі коливання, амплітуда яких внаслідок втрат енергії реальною коливальною системою зменшується з часом. Найпростішим механізмом зменшення енергії коливань є її перетворення в теплоту внаслідок тертя в механічних коливальних системах, а також омічних втрат і випромінювання електромагнітної енергії в електричних коливальних системах.

Закон затухання коливань визначається властивостями коливальних систем. Як правило розглядають лінійні системи — ідеалізовані реальні системи, у яких параметри, що визначають фізичні властивості системи, у ході процесу не змінюються. Лінійними системами є, наприклад, пружинний маятник при малих деформаціях пружини (в межах дії закону Гука), коливальний контур, індуктивність, ємність і опір якого не залежать ні від струму в контурі, ні від напруги. Різні по своїй природі лінійні системи описуються ідентичними лінійними диференціальними рівняннями, що дозволяє підходити до вивчення коливань різної фізичної природи з єдиної точки зору.

Диференціальне рівняння вільних затухаючих коливань лінійної системи задається у вигляді

(2.14)

де x — коливна величина, яка описує той або інший фізичний процес, — коефіцієнт затухання,ω₀ — циклічна частота вільних незатухаючих коливань тієї ж коливальної системи, тобто при (при відсутності втрат енергії).

Щоб знайти розв’язок рівняння (2.14) слід фізичну величину х виразити через нову змінну z відповідно до рівняння

(2.15)

де z = z (t). Після підстановки першої і другої похідних від рівності (2.15) в рівняння (2.14) одержимо

(2.16)

Розв’язок рівняння (2.16) залежить від знака коефіцієнта перед шуканоювеличиною. Розглянемо випадок, коли цей коефіцієнт позитивний, тобто _.

Тоді одержимо рівняння типу

(2.17)

де

. (2.18)

Розв’язком рівняння (2.17) є рівняння типу (1.9):

(2.19)

Після підстановки (2.19) у (2.15) для випадку малих затухань _{одержуємо розв’язок рівняння (2.14) в такому вигляді:}

(2.20)

де ─амплітуда затухаючих коливань, А_о - початкова амплітуда.

Залежність (2.20) показана на рис. 11 суцільною лінією, а амплітуда коливань — пунктирними лініями.

Проміжок часу , протягом якого амплітуда затухаючих коли- вань зменшується у е разів, називається часом релаксації.

Затухання порушує періодичність коливань, тому затухаючі коливання не є періодичними, а тому до них поняття періоду або частоти незастосовне.

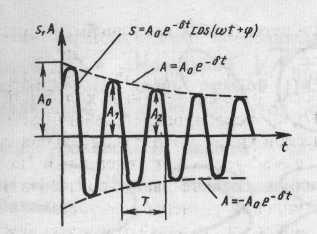
Рис. 11

Однак якщо затухання мале, то можна умовно користуватися поняттям періоду як проміжку часу між двома наступними максимумами (або мінімумами) коливної фізичної величини (рис. 11).

Період затухаючих коливань з урахуванням формули (2.18) дорівнює

(2.22)

Якщо Α (t) і Α (t + T) — амплітуди двох послідовних коливань, які відповідають моментам часу, що відрізняються на один період, то їх відношення

,

називається декрементом затухання, а його логарифм

(2.23)

називається логарифмічним декрементом затухання; N — число коливань,

які виконує коливна система за час зменшення амплітуди в е разів.

Для характеристики коливальної системи користуються поняттям добротності яка при малих значеннях логарифмічного декремента є помноженому на 2відношенню повної накопленої системою енергії до середніх втрат енергії цією системою за час в один період, тобто

(2.24)

де W ─ повна енергія системи; ΔW(T) ─ середні втрати енергії системою за час в один період (t=T).

Повна енергія коливної системи в момент часу t дорівнює

(2.25)

Енергія коливної системи через час в один період

(2.26)

Втрати енергії системою за час в один період дорівнюють

(2.27)

Добротність коливної системи одержимо, поділивши (2.25) на (2.27) і помноживши одержану величину на 2.

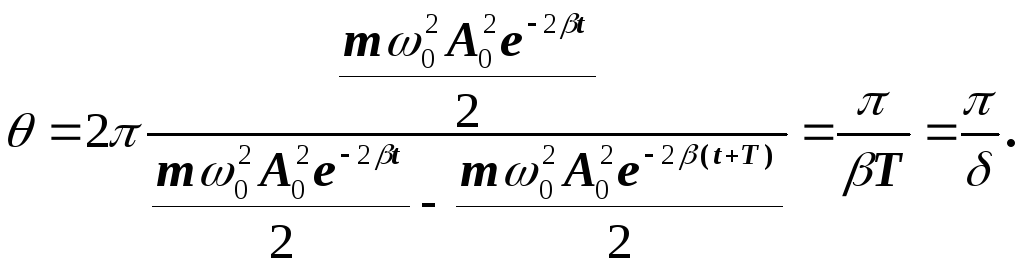(2.28)

У випадку, коли період коливаньT приймають рівним T₀.

У виразі (2.28) враховано, що відношення

1. Вільні затухаючі коливання пружинного маятника. Для пружинного маятника масою т, який виконує малі коливання під дією пружної сили F = - кх, сила тертя пропорційна швидкості, тобто

де m — коефіцієнт опору; знак мінус указує на протилежні напрямки сили тертя і швидкості.

За даних умов закон руху маятника буде мати вигляд

(2.29)

Введемо позначення і, одержимо диференціальне рівняння для затухаючих коливань пружинного маятника:

(2.30)

З виразів (2.29) і (2.30) випливає, що маятник коливається за законом

(2.31)

з частотою

. (2.32)

Добротність пружинного маятника, згідно (2.28) дорівнює

2. Вільні затухаючі коливання в електричному коливальному контурі

Диференціальне рівняння вільних затухаючих коливань заряду в коливальному контурі (при ) має вигляд

(2.33)

Коефіцієнт затухання й власна циклічна частота в цьому випадку будуть дорівнювати

(2.34)

З урахуванням позначень (2.34) диференціальне рівняння (2.33) матиме вигляд:

(2.35)

Розв’язком рівняння (2.35) а також рівняння (2.33) є функція

(2.36)

Циклічна частота коливань у цьому випадку буде дорівнювати

(2.37)

При R = 0 формула (2.37) переходить у

Логарифмічний декремент затухання в цьому випадку визначається формулою , а добротність коливального контуру

На закінчення відзначимо, що при збільшенні коефіцієнта затухання періодзатухаючих коливань зростає і при = ω₀ перетворюється в безмежність, тобто рух перестає бути періодичним. У даному випадку коливна величина прибуде мати асимптотичне наближення до нуля. Такий процес не є коливальним. Він називається аперіодичним.

Якщо втрати енергії реальною коливальною системою поповнювати від зовнішнього джерела, то коливання стануть незатухаючими. Особливо важливими і широко застосовними є так звані автоколивання — незатухаючі коливання, які підтримуються в дисипативній системі за рахунок постійного зовнішнього джерела енергії, причому властивості цих коливань визначаються самою системою. До дисипативної системи відноситься будь-яка система, яка втрачає або розсіює енергію в навколишній простір.

Автоколивання принципово відрізняються від вільних незатухаючих коливань, які відбуваються без дії зовнішніх сил, а також від вимушених коливань, що відбуваються під дією періодичної сили. Автоколивальна система сама керує зовнішніми впливами, забезпечуючи погодженість надходження енергії певними порціями в потрібний момент часу (у такт із її коливаннями).

Прикладом автоколивальної системи може бути механічний годинник. Храповий механізм підштовхує маятник у такт із його коливаннями. Енергія, передана в цьому випадку маятнику, береться або за рахунок пружини, що розкручується, або за рахунок опускання вантажу. Коливання повітря в духових інструментах і органних трубах також виникають внаслідок автоколивань, підтримуваних повітряним струменем.

Автоколивальними системами єтакож двигуни внутрішнього згоряння, парові турбіни, лампові генератори, тощо.

Лекція 3. Вимушені механічні й електромагнітні коливання