1) Дослідник вносить гіпотезу про структуру скриньки

Розглядаючи експериментально отримані дані, припустимо, що вони підпорядковуються лінійної гіпотези, тобто вихід Y залежить від входу X лінійно, тобто гіпотеза має вигляд: (рис. 6.6).

2) Визначення невідомих коефіцієнтів і моделі

Лінійна одновимірна модель (рис. 6.7).

 

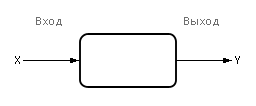
Рис. 6.7 - Одновимірна модель чорного ящика

Для кожної з n знятих експериментально точок обчислимо помилку між експериментальним значенням і теоретичним значенням , лежачим на гіпотетичній прямій A₁X +A₀ (див. рис. 6.6):

, ,

, ,

Помилки для всіхn точок слід скласти. Щоб позитивні помилки не компенсували в сумі негативні, кожну з помилок зводять у квадрат і складають їх значення в сумарну помилку F вже одного знака:

, ,

 

Мета методу - мінімізація сумарної помилки за рахунок підбору коефіцієнтів. Іншими словами, це означає, що необхідно знайти такі коефіцієнти лінійної функції , щоб її графік проходив як можна ближче одночасно до всіх експериментальних точок. Тому даний метод називається методом найменших квадратів.

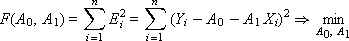
Сумарна помилка є функцією двох змінних , тобто, змінюючи які, можна впливати на величину сумарної помилки (див. рис. 2.4).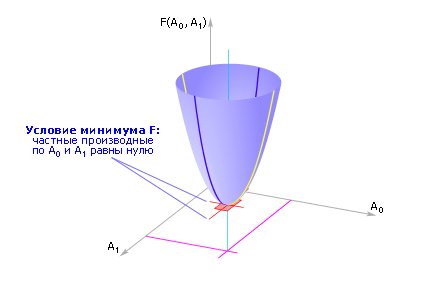

Рис. 6.8 - Приблизний вид функції помилки

Щоб сумарну помилку мінімізувати, знайдемо частинны похідні від функції Е по кожній змінный і прирівняємо їх до нуля (умова екстремуму):

 

 

Після розкриття дужок отримаємо систему з двох лінійних рівнянь:

 

 

Для знаходження коефіцієнтів методом Крамера представимо систему в матричній формі:

.

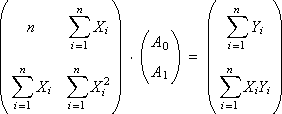Рішення має вигляд:

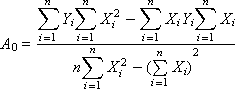
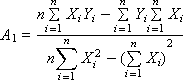
3) Перевірка

Щоб визначити, приймається гіпотеза чи ні, потрібно, по-перше, розрахувати помилку між точками заданої експериментальної і отриманої теоретичної залежності і сумарну помилку:

, ,

 

І, по-друге, необхідно знайти значення σ за формулою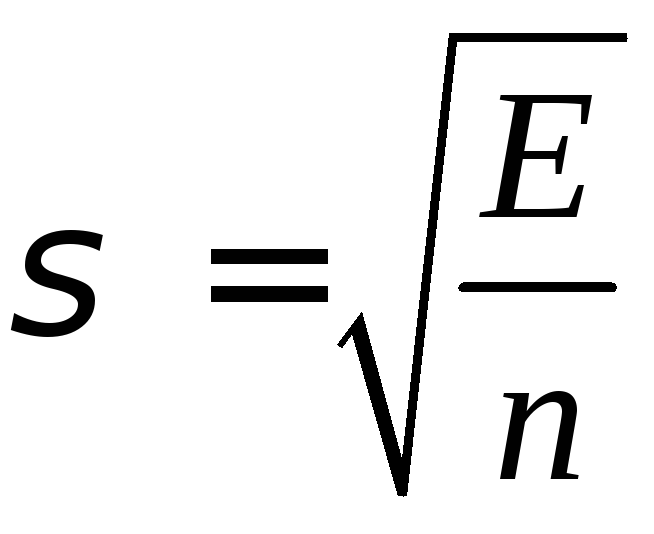, де E - сумарна помилка, n - загальне число експериментальних точок.

Якщо в смугу, обмежену лініями і (рис. 6.9), потрапляє 68.26% і більше експериментальних точок , то висунута нами гіпотеза приймається. В іншому випадку вибирають більш складну гіпотезу або перевіряють вихідні дані. Якщо потрібна велика впевненість в результаті, то використовують додаткову умову: в​​смугу, обмежену лініями і, повинні потрапити 95.44% і більше експериментальних точок .

Рис. 6.9 - Дослідження допустимості прийняття гіпотези

Відстань S пов'язана з σ наступним співвідношенням:

S = σ / sin (β) = σ / sin (90 ° - arctg (A1)) = σ / cos (arctg (A1)),

що проілюстровано на рис. 6.10.

Рис. 6.10 - Зв'язок значень σ і S