Завдання 4

Для оцінювання результату опосередкованого вимірювання величини виконані по 9 вимірювань величинX, Y і отримані результати Х=26,16; 26,75; 25,76; 26,44; 25,84; 25,52; 26,47; 26,39; 27,51 та У=16,11; 16,41; 15,29; 15,91; 15,71; 16,33; 16,32; 16,83; 16,29. Відомі середньоквадратичні відхилення (с. к. в.) похибок вимірювань цих величин: Оцінити результат вимірювання U, вважаючи що результати вимірювань X,Y взаємно незалежні. Оцінити довірчі границі похибки вимірювання U з =0,9. Записати результат.

Розв’язання:

Похибку опосередкованого вимірювання шукаємо за похибками прямих вимірювань. Зокрема, відносна похибка , А абсолютна похибка непрямого вимірювання (див. задачу3)

Результати рівно точних взаємнонезалежних спостережень величин Х та У містять випадкові похибки. Тому найкращою оцінкою кожної з безпосередньо вимірюваних величин (Х та У) та опосередкованої величини U будуть їх середні значення, тобто

За визначенням абсолютна похибка тут- істинне, дійсне та середнє значення величиниU, яку можна оцінити значеннями за прямими спостереженнямита.

Тому дисперсія абсолютної похибки усередненого результату посереднього вимірювання

Так само пов’язані і їх незміщені оцінки

Своєю чергою дисперсія похибок кожної з усереднених величин тадорівнює сумі незміщеної оцінки дисперсії середнього випадкових спостережень та дисперсії інструментальної похибки відповідного вимірювального приладу, а саме:

Незміщені оцінки дисперсії спостережень

А дисперсій відповідних середніх значень та

Звідси

Для =0,9 йn=9 гарантійний коефіцієнт . Звідси результат опосередкованого вимірювання

Завдання 5

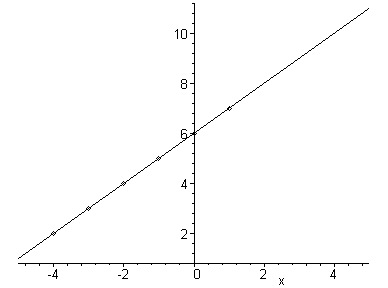
Для результатів вимірювань величин Х= -4; -3; -2; -1; 0; 1 та У=2; 2.97; 3.99; 4.99; 6.02; 7.05 за допомогою методу найменших квадратів (МНК) визначити коефіцієнти лінійної залеж­ності між ними.

Розв'язання:

За умовою вважається, що залежність між величинами Y та Х є лінійною, тобто

Y=kX+b.

Необхідно знайти два невідомі параметри k й Ь, опрацьовуючи набори результатів спостережень {х,} та {у,} за методом найменших квадратів. Сформуємо відповідні рівняння, а саме: знайдемо часткові похідні функції Y за невідомими параметрами

Одержимо систему двох рівнянь з двома невідомими, а саме:

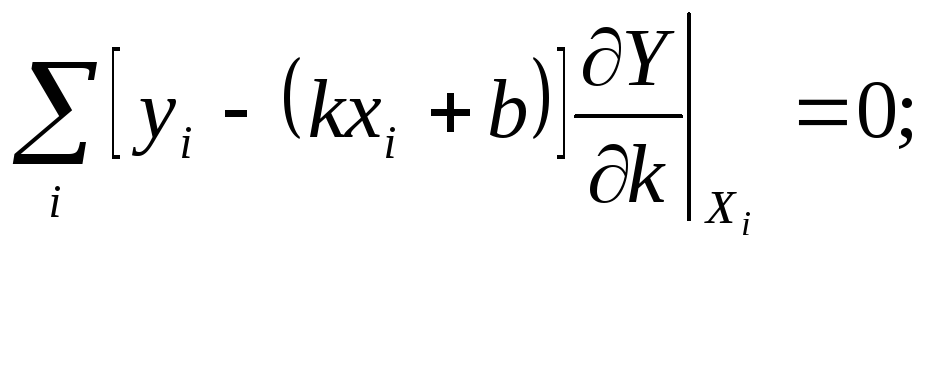
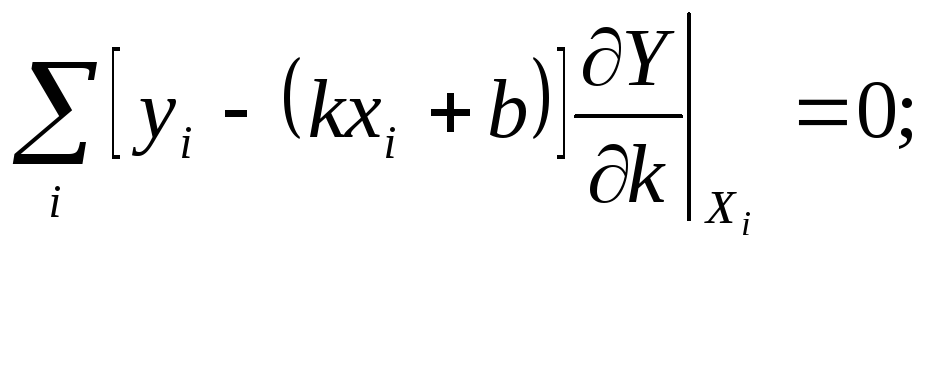
Звідси:

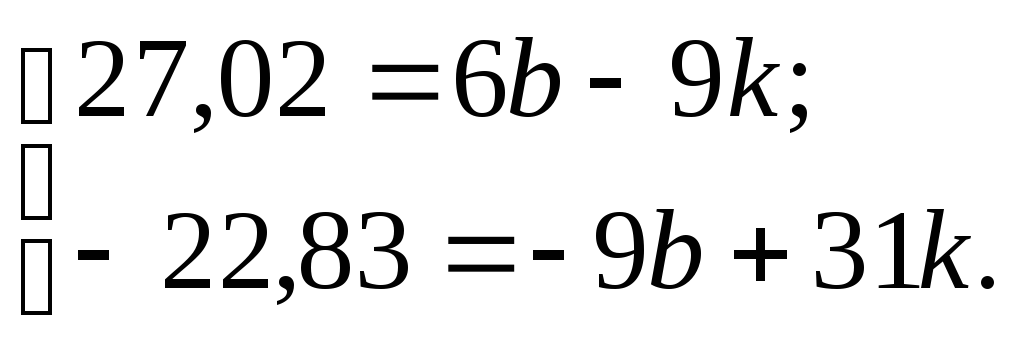
Знайдемо k=1,b=6. Отже Y=X+6.

Завдання 6

Сформуйте систему нормальних рівнянь за методом найменших квадратів для результатів сукупних вимірювань. Оцінити СКВ. Знайти нев’язки. Записати результат вимірювання.

Результати сукупних вимірювань див. табл. 6

Варіант	x1+x2x+x3+x4	x2+x3	x1+x2	x3+x4	x1+x2+x3	x1+x3+x4	x1+x4+x3	x2+x4	x3+x1
18	14,13	8,14	8,17	6,15	9,13	7,26	7,19	12,17	2,15

Розв’язання

Складемо систему нормальних рівнянь:

,

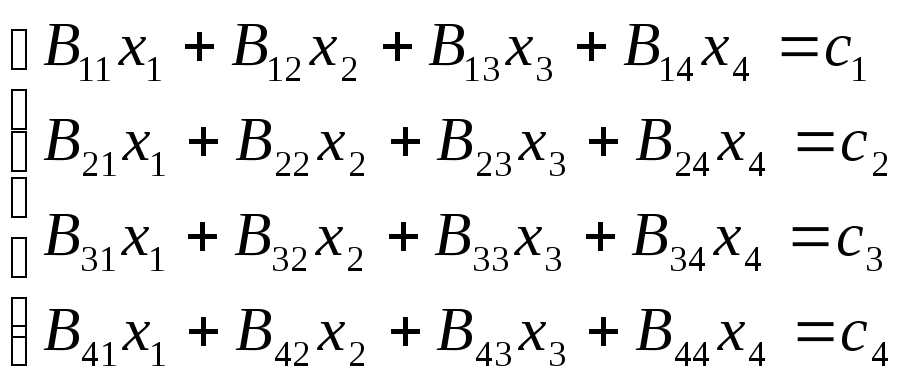де коефіцієнти

= 6,

= 5,

= 7,

= 5,

= 3,

= 5,

= 3,

= 2,

= 3,

= 4,

= 14,13+8,17+9,13+7,26+7,19+2,15=48,03,

= 14,13+8,14+8,17+9,13+12,17 = 51,74,

= 14,13+8,14+6,15+9,13+7,26+7,19+2,1,5 = 54,15

= 14,13+6,15+7,26+7,19+12,17 = 46,9.

Врахувавши значення даних коефіцієнтів система нормальних рівнянь матиме вигляд:

.

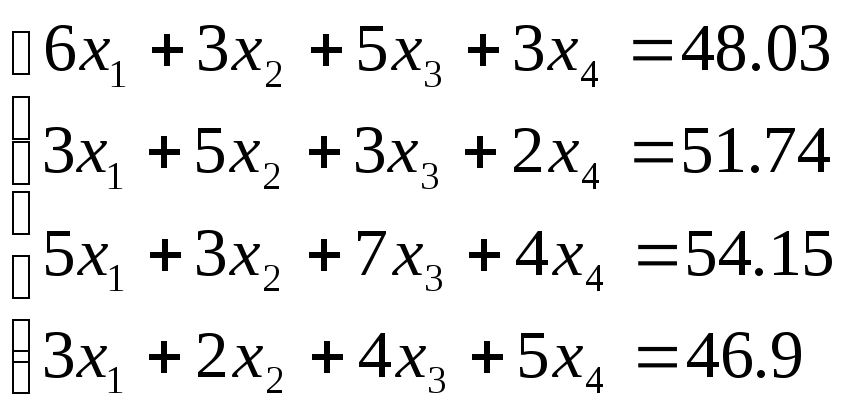Головний визначник цієї системи D = 156.

Найбільш ймовірні значення невідомих дорівнюють:

.

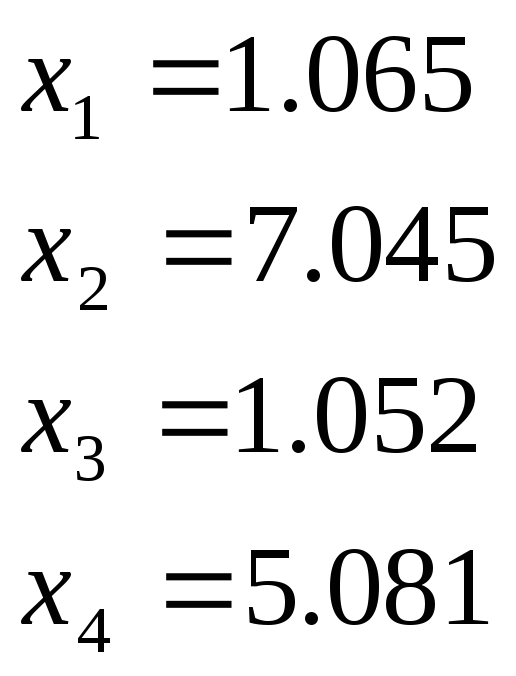Підставляємо значення найбільш ймовірних значень до умовних рівнянь:

x₁ + x₂ + x₃ + x₄ = 1.065 + 7.045 + 1.052 + 5.081 = 14.243,

x₂ + x₃ = 7.045 + 1.052 = 8.097,

x₁ + x₂ = 1.065 + 7.045 = 8.11,

x₃ + x₄ = 1.052 + 5.081 = 6.133,

x₁ + x₂ + x₃ + x₄ = 1.065 + 7.045 + 1.052 = 9.162,

x₁ + x₂ + x₃ = 1.065 + 1.052 + 5.081 = 7.098,

x₁ + x₃ + x₄ = 1.065 +1.052 + 5.081 = 7.198,

x₁+x₃+x₄= 1.065 + 5.081 + 1.052 = 7.198,

x₂+x₄= 7.045 + 5.081 = 12.126,

x₁+x₃= 1.052 + 1.065 = 2.117.

Знаходимо нев´язки

,

Знайдемо границі довірчого інтервалу

,

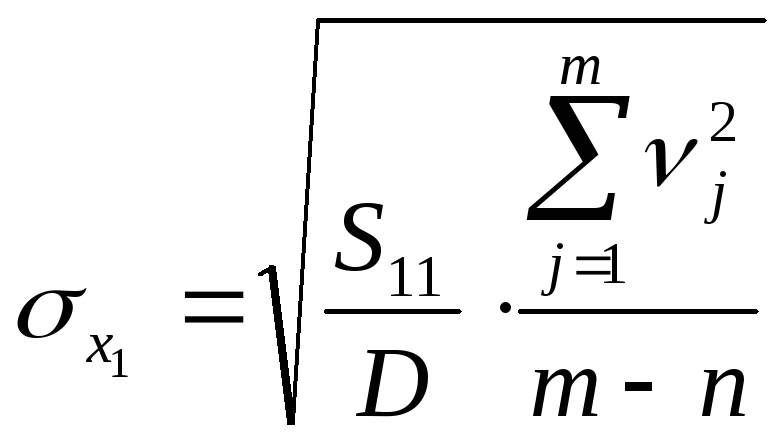і аналогічно для інших невідомих. Для цього розрахуємо значення ад’юнктів.

S₁₁=70, S₂₂=72, S₃₃ = 72, S₄₄ = 52

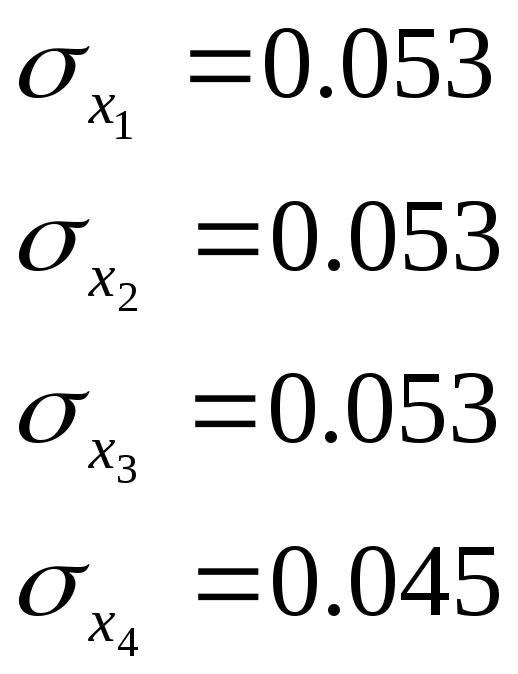
Для m-n=5 та ймовірності Р=0,95 коефіцієнт Ст´юдента дорівнює t_p = 2.571

Розрахуємо границі довірчого інтервалу

Отже, результат вимірювання

Розрахунки реалізовані за допомогою математичного пакету Mathcad і наведені у додатку.