2.6. Определение момента инерции маховика

Из графиков изменения кинематической энергии ∆T и приведенных моментов инерции звеньев механизма I_пр, исключив параметр φ, получим график «Энерго-масс».

Построение этого графика производится в следующем порядке: через каждую точку абсцисс кривой графика I_пр проводим вертикальные прямые, до пересечения с соответствующими горизонтальными прямыми. Получаемые точки соединяем последовательно, получим график «Энерго-масс».

К графику «Энерго-масс» проводятся касательные. Тангенсы наклонных прямых будут:

;

- заданный коэффициент неравномерности хода.

На оси I_пр касательные отсекают отрезок ab , который в масштабе

выражает значение момента инерции маховика.

ab - отрезок, отсекаемый касательными, мм, ( ab = 259мм )

Определяем значение момента инерции махового колеса, кг м²

2.7. Определение видов и размеров маховика.

Принимаем диаметр D= 1,3м, тогда масса маховика:

Определяем ширину маховика:

где γ - удельный вес материала маховика (γ=7100÷7300)

В масштабе 1:50 на листе 2 вычерчиваем маховик, в виде поперечного сечения диска.

3. Синтез плоских кулачковых механизмов.

3.1.Определение минимального радиуса кулачка

Ведущее звено в кулачковом механизме называется кулачком, ведомое толкателем. Толкатель совершает прямолинейные возвратно-поступательные движения и касается кулачка во время движения.

Задача синтеза кулачковых механизмов состоит в том, чтобы построить профиль кулачка, удовлетворяющий поставленным технологическим процессам и требованиям.

Кулачковый механизм предназначен для задания закона движения выходного звена.

Синтез кулачкового механизма начинаем с построения графика (график аналогового ускорения толкателя), которая дана по условию.

По оси откладываем угол,,в масштабе

Где

До значения 0,3 Ф₁=95̊ функция =-изменяется по косинусоиде. Строим косинусоиду с амплитудой, которую принимаем равной 67 мм. После значения 27̊ функция уходит в отрицательную область и получается над осью φ у нас геометрическая фигура – треугольник, площадь которого должна быть примерно равна площади построенного участка косинусоиды.

Далее методом графического интегрирования графика , построим график. Полюсное расстояниепринимаем равным 50мм.

Далее методом графического интегрирования графика , построим график. Полюсное расстояниепринимаем равным 50мм.

Определяем масштабы построенных графиков:

Масштаб графика S-φ равен:

Масштаб графика равен:

Масштаб графика равен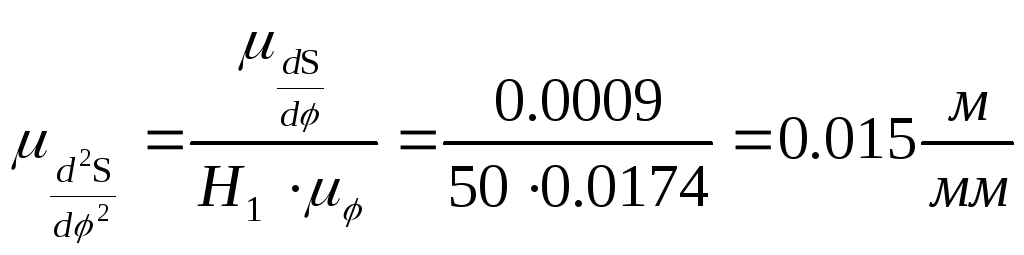

После построения диаграмм движения толкателя определяем минимальный радиус кулачка. Для этого наложим диаграммы иодну на другую и просуммируем их. Для этого ординатыdS, d²S определяем в масштабе µs, используя формулу: .

После построения минимальный радиус кулачка ищется в отрицательной зоне:

Для нашего случая a=4мм, δ=мм

(a + δ) ·µs=(4+12,5)·0,0008=0,0132м

Принимаем 13,2 мм. Для построения кулачка увеличиваю его радиус в 4,5 раза

3.2. Профилирование кулачка

Из центра О1 проводим прямую О1К вертикально вверх и из того же центра проводим окружность радисом r0= 60мм

Определяем масштаб µl:

µl=

От точки пересечения окружности с осью ОК откладываем величины в масштабе подъёмов толкателя 0-6 положений и положений опусканий, они у нас будут совпадать, т.к. Ф1 = Ф3.

Также от оси ОК откладываем углы Ф1 = 95°, Ф₂ = 23°и Ф3 = 95° через точку О. Затем углы Ф1 и Ф3 делим на столько же равных частей, на сколько делили эти же углы на графике аналога ускорений; для нашего случая делим на 6 частей. Затем проводим от величин подъемов и опусканий толкателя дуги до пересечения с лучами, делящими наши углы на равные части, соответственно. К точкам пересечения дуг и лучей строим перпендикуляры, которые являются касательными к профилю кулачка.

Чтобы отложить величины подъёмов и опусканий толкателя для построения профиля кулачка, нужно сначала перевести в масштаб µl