1.4. Планы ускорений

Последовательность построения плана ускорений также определяется формулой строения механизма: сначала строим план для кривошипа 2, затем для группы Ассура (3,4) и, наконец, для группы (5,6).

У кривошипа 2 полное ускорение точки А равно геометрической сумме двух составляющих: нормального ускорения, направленного к центру вращения, то есть от точки А к точке О, и тангенциального, направленного перпендикулярно ОА в сторону, соответствующую направлению углового ускоренияε₂. Следовательно,

=.

Так как принято, что . Следовательно, тангенциальное ускорение=0.

Ускорение изобразим отрезкомπа равное 100 мм. Тогда масштабный коэффициент ускорения будет соответствовать рекомендуемым значениям.

Ускорение точки В определяется совместным решением системы векторных уравнений.

Нормальная составляющая направлена по положению шатуна АВ от точки В к точке А.

- касательная составляющая направлена перпендикулярно шатуну АВ

На плане ускорений из конца вектора проводится линия действия , на которой в направлении от точки В к точке А откладывается отрезок:

Через конец вектора проводится линия действия, перпендикулярно этому вектору.

Аналогичным образом получим относительно точкиО.

Определяем ускорение точки D

Умножая векторы ускорений на масштаб, получим их численные значения:

Определяем угловые ускорения шатунов рад/с²:

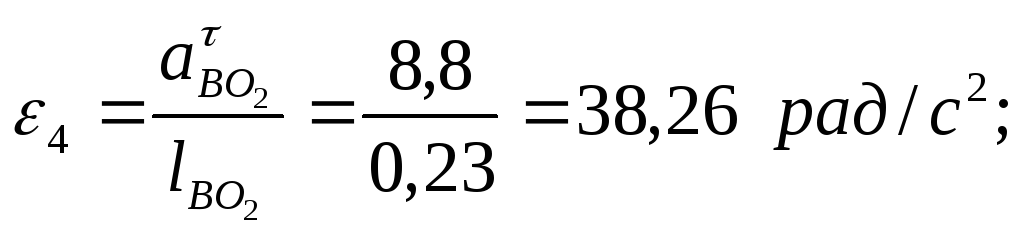
Рис 3. План ускорений

1.5. Силовой анализ

Динамический анализ механизма состоит в определении реакции в кинематических парах и уравновешивающих сил, обеспечивающий заданныйзакон движения механизма. Динамический анализ плоских механизмов обычно производится кинетостатическим методом.

По этому методу механизм раскладывается на структурные группы (группы Ассура и ведущее звено). Прикладываем к ним задаваемые силы (силы полезного сопротивления или движущие силы) и искомые реакции в кинематических парах. Составляем и решаем уравнения статики.

Динамический анализ ведется от последней группы Ассура к ведущему звену, для которого определяются кроме реакции стойки и уравновешивающая сила.

Определяем силы тяжести звеньев:

;

;

;

;

Направление силы тяжести вертикально вниз. Точки приложения центра масс звеньев

Определяем силы и моменты инерции звеньев:

кг·м²; кг·м²;

кг·м²;

Векторы Р_из Р_и4 и Р_и5, противоположно направлены , приложеныв точках приложения центр масс S₃ , S₄ и S₅. Моменты ,и противоположно направлены ,и.

Определение реакций группы Ассура 5-6

Рис.4 Группа Ассура 5-6

Вместо удаляемых связей прикладываем реакции в шарнире В – R₃₅ , на ползун D – R_16- Неизвестная по направлению и величине R₄₅ показывается в виде двух составляющих: и, нормальная составляющаянаправляется по направлению шатуна, тангенциальная - перпендикулярно. Реакция R₁₆ известна по направлению: линия действия перпендикулярна направляющим. Вектора сил на схеме показываются без соблюдения масштаба.

Для определения реакции R₄₅ составим уравнение суммы моментов относительно точки В.

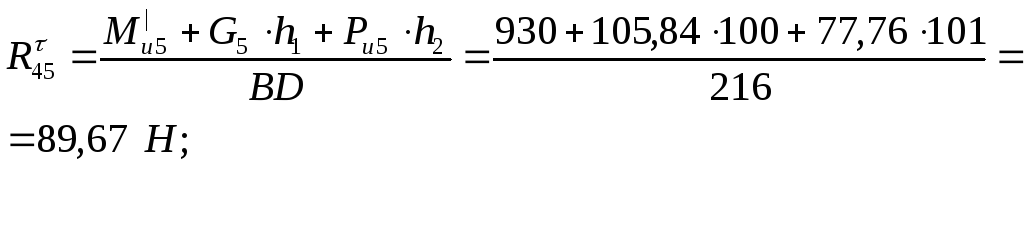
Составим уравнение равновесия для группы Ассура:

Векторное уравнение решается графически. Из уравнения находим реакцию

Выбираем масштаб плана сил - и определим длины векторов в мм на плане для всех известных сил:

Действительную величину реакции определяем из плана сил:

Из условия равновесия ползуна D находим R₅₆: