1. Структурный анализ механизма

Кинематическому анализу механизма обычно предшествует структурный анализ, который состоит в определении степени подвижности и структурных групп.

Степень подвижности показывает потребное количество задаваемых законов движения и число начальных звеньев. При ее определении выявляются звенья, устанавливаются их названия, число и класс кинематических пар, а также пассивные связи, если такие имеются.

Рычажные механизмы расчленяются на структурные группы — группы Ассура, и начальные звенья. Класс, порядок и вид структурных групп определяют методы и последовательность кинематического и силового анализа.

Степень подвижности плоских механизмов определяется по формуле Чебышева П. Л., которая для рычажных механизмов имеет вид:

W=3n-2p₅ = 3·5-2·7 = 1,

где п - число подвижных звеньев; p₅ - число кинематических пар пятого класса.

К начальному звену 1 и стойке 0 последовательно присоединены две группы Ассура: (3,4) – второго класса, второго порядка, первого вида и (5,6) – второго класса, второго порядка, второго вида, значит, данный механизм относится ко второму классу. Порядок кинематического исследования механизма определяется формулой его строения: I (0,1)→ II (2,3) → II (4,5). План механизма построен в масштабе:

Рис 1. Группы Ассура

1.2. Построение 12 планов механизма.

В соответствии с заданием основные звенья механизма имеют следующие параметры: ,, .

Построение плана положений звеньев механизма производится методом засечек. За начальное (нулевое) положение механизма понимается такое, при котором ведомое звено находится в одном из крайних положений. В этом положении скорость ведомого звена равна нулю. Для построения других положений механизма берется 12 положений механизма, соответствующих углам поворота через 30^о. Положения кривошипа обозначаются порядковым номером, начиная с нулевого, в направлении угловой скорости 2.

Планы механизма строятся в масштабе, который определяется как отношение реальной длины кривошипа в метрах (м) к длине его отрезка на

чертеже в миллиметрах (мм):

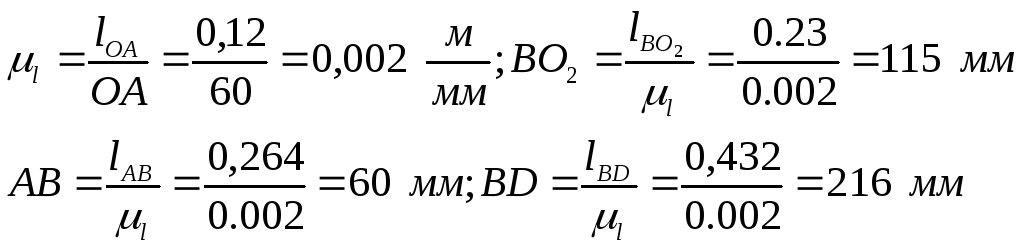
1.3. Планы скоростей.

Планами скоростей и ускорений механизма называется векторное изображение этих кинематических параметров для соответствующего положения механизма.

Метод планов основан на теореме о разложении движения, согласно которой сложное движение любого звена можно разложить на переносное – поступательное и относительное – вращательное.

Угловая скорость кривошипа равна: ω₂ =13 (1/с).

У кривошипа определяем скорость точки А:

().

Эту скорость изобразим отрезком pа=50 мм (p – полюс плана скоростей).

Определяем масштабный коэффициент скоростей:

Вектор откладываем перпендикулярно к кривошипу в данном положении и направляем в сторону его вращения.

Рисунок2. -План скоростей

находим, используя свойство подобия

Используя план скоростей, получаем следующие значения абсолютных и относительных скоростей точек для второго положения:

Определяем угловые скорости ω₃ , ω₄, ω₅, звеньев 3, 4 и 5:

Таблица 1- Расчетные данные и численные значения скоростей

Поло-жение меха-низма	0	1	2	3	4	5	6	7	8	9	10	11
bd, мм	0	12	19	23	18	3	18	27	7	33	55	21
pb, мм	0	15	26	38	48	55	57	47	13	184	87	26
аb, мм	50	53	52	40	31	21	12	4	63	194	45	29
pd, мм	0	5	12	22	37	53	64	52	13	199	47	9
рs3, мм	26	24	30	39	47	52	53	48	20	102	67	36
ps4, мм	0	7,5	13	19	24	27,5	28,5	28,5	6,5	92	43,5	13
ps5, мм	0	8,5	17	27	41	54	60	47,5	12	191	65	15,5
A м/с	1,56
DB, м/с	0	0,36	0,57	0,69	0,54	0,09	0,54	0,81	0,21	0,99	1,65	0,63
B, м/с	0	0,45	0,78	1,14	1,44	1,65	1,71	1,41	0,39	5,52	2,61	0,78
AB, м/с	1,5	1,59	1,56	1,2	0,93	0,63	0,36	0,12	1,89	5,82	1,35	0,87
D,м/c	0	0,15	0,36	0,66	1,11	1,59	1,92	1,56	0,39	5,97	1,41	0,27
S3, м/с	0,78	0,72	0,9	1,17	1,41	1,56	1,59	1,44	0,6	3,06	2,01	1,08
s4, м/с	0	0,225	0,39	0,57	0,72	0,825	0,855	0,855	0,195	2,76	1,305	0,39
S5, м/с	0	0,255	0,48	0,81	1,23	1,62	1,8	1,425	0,36	5,73	1,95	0,465
S6, м/с	0	0,15	0,36	0,66	1,11	1,59	1,92	1,56	0,39	5,97	1,41	0,27
ω3, 1/с	5,68	6,02	5,9	4,54	3,52	2,39	1,36	0,45	7,16	22,04	5,11	3,3
ω 4, 1/с	0	1,96	3,39	4,96	6,26	7,17	7,43	6,13	1,7	24	11,35	3,39
ω 5, 1/с	0	0,83	1,32	1,6	1,25	0,21	1,25	1,875	0,48	2,29	3,82	1,46
pa, мм	50
ω2, 1/с	13