Средняя квадратическая

Используется в тех случаях, когда при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин.

Главная сфера её использования – измерение степени колеблемости индивидуальных значений признака относительно средней арифметической (среднее квадратическое отклонение). Кроме этого, средняя квадратическая применяется в тех случаях, когда необходимо вычислить средний величину признака, выраженного в квадратных или кубических единицах измерения (при вычислении средней величины квадратных участков, средних диаметров труб, стволов и т. д.).

Средняя квадратическая рассчитывается в двух формах:

- как простая

(4.21)

как взвешенная

(4.22)

Все степенные средние различаются между собой значениями показателя степени.При этом, чем выше показатель степени, тем большеколичественное значение среднего показателя:

(4.23)

Это свойство степенных средних называется свойством мажорантности средних.

Таким образом, выбор вида среднего показателя оказывает существенное влияние на его численную величину. Выбор вида средней определяется в каждом отдельном случае путем анализа исследуемой совокупности, изучения содержания явления. Степенная средняя выбрана правильно, если на всех этапах вычислений не меняется её логическая формула, т.е. реально сохраняется социально-экономическое содержание усредняемого признака.

Особый вид средних показателей – структурные средние. Они используются при изучении внутреннего строения рядов распределения значений признака. К ним относятся мода и медиана.

Мода и медиана характеризуют значение признака у статистической единицы, занимающей определенное положение в вариационном ряду.

Мода (Mo) - наиболее часто встречаемое значение признака в совокупности. Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и др.

Медиана (Me) - значение признака у статистической единицы, стоящей в середине ранжированного ряда и делящей совокупность на две равные по численности части.

Для дискретных вариационных рядов Mo и Me выбираются в соответствии с определениями: мода - как значение признака с наибольшей частотой\ n_i ; положение медианы при нечетном объеме совокупности определяется ее номером , гдеN – объем статистической совокупности. При четном объеме ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

Медиану используют как наиболее надежный показатель типичного значения неоднородной совокупности, так как она нечувствительна к крайним значениям признака, которые могут значительно отличаться от основного массива его значений. Кроме этого, медиана находит практическое применение вследствие особого математического свойства: .

Рассмотрим определение моды и медианы на следующем примере:

Имеется ряд распределения рабочих участка по уровню квалификации. Данные приведены в таблице 4.4.

Таблица 4.4 - Распределения рабочих участка по уровню квалификации

№ группы	Разряд рабочих	Число рабочих	Накопленная частота
1	1	3	3
2	2	5	8
3	3	9	17
4	4	14	31
5	5	10	41
6	6	9	50
Всего	-	50	-

Мода выбирается по максимальному значению частоты: при n_max = 14, Mo = 4, т.е. чаще всего встречается 4-ый разряд. Для нахождения медианы Me определяются центральные единицы (N +1)/2 . Это 25 и 26-ая единицы. По накопленным частотам определяется группа, в которую попадают эти единицы. Это 4-ая группа, в которой значение признака равно 4. Таким образом, Me = 4, это означает, что у половины рабочих разряд ниже 4-го, а у другой – выше четвертого.

В интервальном ряду значения Mo и Me вычисляются более сложным путем.

Мода определяется следующим образом:

• По максимальному значению частоты определяется интервал, в котором находится значение моды. Он называется модальным.

• Внутри модального интервала значение моды вычисляется по формуле:

(4.24)

где - нижняя граница модального интервала;

a_Мо - ширина модального интервала;

n_Мо , n_Мо-1, n_Мо+1 - соответственно частоты модального, предмодального (предшествующего модальному) и постмодального (следующего за модальным) интервалов.

Для расчета медианы в интервальных рядах используется следующий подход:

• По накопленным частотам находится медианный интервал.

Медианным называется интервал, содержащий центральную единицу.

• Внутри медианного интервала значение Me определяется по формуле:

(4.25)

где - нижняя граница медианного интервала;

a_Ме -ширина медианного интервала;

N – объем статистической совокупности;

N _Ме-1- накопленная частота предмедианного интервала;

n _Ме - частота медианного интервала.

Расчет моды и медианы для интервального ряда распределения рассмотрим на примере ряда распределения рабочих по стажу (табл. 4.5).

Таблица 4.5 - Распределение рабочих участка по стажу

№ группы	Интервал		аi	ni	Ni
1	0	4	4	6	6
2	4	8	4	8	14
3	8	12	4	11	25
4	12	16	4	13	28
5	16	20	4	6	44
6	20	24	4	4	48
7	24	28	4	2	50
Всего	0	28	28	50	-

Расчет Mo:

• Максимальная частота n_max = 13, она соответствует четвертой группе, следовательно, модальным является интервал с границами 12 – 16 лет.

• Моду рассчитаем по формуле:

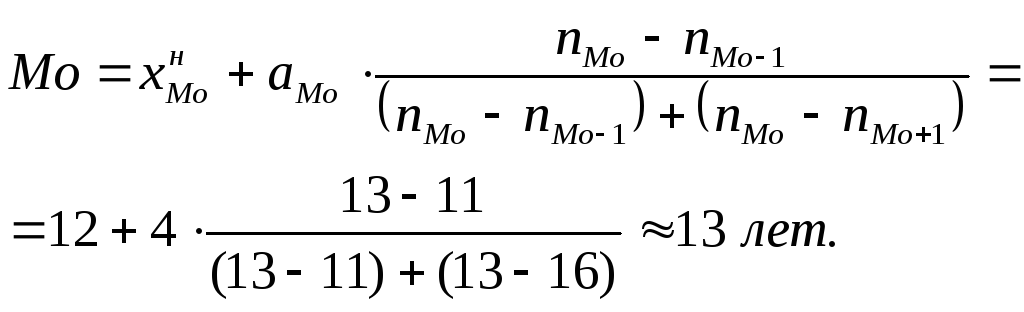
Чаще всего встречаются рабочие со стажем работы около 13 лет.

Мода не находится в середине модального интервала, она смещена к его нижней границе, связано это со структурой данного ряда распределения (частота предмодального интервала значительно больше частоты постмодального интервала).

Расчет медианы:

• По графе накопленных частот определяется медианный интервал. Он содержит 25 и 26-ую статистические единицы, которые находятся в разных группах – в 3-ей и 4-ой. Для нахождения Me можно использовать любую из них. Расчет проведем по 3-ей группе:

Такое же значение Me можно получить при её расчете по 4-ой группе:

При сдвоенном центре Me всегда находится на стыке интервалов, содержащих центральные единицы. Вычисленное значениеMe показывает, что у первых 25 рабочих стаж работы – менее 12 лет, а у оставшихся 25-ти, следовательно, - более 12 лет.

Моду можно определить графически по полигону распределения в дискретных рядах, по гистограмме распределения – в интервальных, а медиану - по кумуляте.

Для нахождения моды в интервальном ряду правую вершину модального прямоугольника нужно соединить с правым верхним углом предыдущего прямоугольника, а левую вершину – с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.

Для определение медианы высоту наибольшей ординаты кумуляты, соответствующей общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.

Кроме Mo иMe в вариантных рядах могут быть определены и другие структурные характеристики – квантили. Квантили предназначены для более глубокого изучения структуры ряда распределения.Квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности. Различают следующие виды квантилей:

- квартили – значения признака, делящие упорядоченную совокупность на 4 равные части;

- децили – значения признака, делящие совокупность на 10 равных частей;

- перцентели - значения признака, делящие совокупность на 100 равных частей.

Таким образом, для характеристики положения центра ряда распределения можно использовать 3 показателя: среднее значениепризнака,мода, медиана.

При выборе вида и формы конкретного показателя центра распределения необходимо исходить из следующих рекомендаций:

- для устойчивых социально-экономических процессов в качестве показателя центра используют среднюю арифметическую. Такие процессы характеризуются симметричными распределениями, в которых

= Me = Mo;

- для неустойчивых процессов положение центра распределения характеризуется с помощью Mo илиMe. Для асимметричных процессов предпочтительной характеристикой центра распределения является медиана, поскольку она занимает положение между средней арифметической и модой.