Средняя арифметическая взвешенная
Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным или вариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднюю сгруппированных величин.
(4.12)
где
-
частость, т. е. удельный вес статистических
единиц, обладающих определенным значением
признака в общем объеме совокупности.
Пример: рассчитать среднюю продажную цену товара по данным, приведенным в таблице 4.1:
Таблица 4.1 - Объём продаж и цена товара А в магазинах города
|
Магазины |
Цена единицы товара, руб. |
Объем продаж, шт. |
|
Космос |
20 |
25000 |
|
Ариадна |
18 |
40000 |
|
Вега |
19 |
40000 |
|
Итого |
? |
105000 |
Использовать среднюю арифметическую простую в данном случае нельзя, так как в разных магазинах продано разное количество товара А. Для расчёта средней продажной цены товара А. следует применить среднюю арифметическую взвешенную:
При применении средней арифметической простой средняя продажная цена товара составляла бы: х = (20 + 18 + 19) / 3 = 19 руб. , т.е. оказалась бы завышенной.
Определение средней арифметической взвешенной по интервальному ряду
Сначала находят центры (середины) интервалов, а затем их умножают на веса, произведения суммируют и делят на сумму весов.
Пример.Требуется определить среднемесячную заработную плату одного рабочего по следующим данным (табл. 4.2)
Таблица 4.2 – Исходные данные:
|
Исходные данные: |
Расчетные данные: | ||
|
месячная зарплата, руб. |
Число рабочих, чел. |
Середины интервалов |
- |
|
xi |
fi |
|
|
|
4000-5000 |
10 |
4500 |
45000 |
|
5000-6000 |
20 |
5500 |
110000 |
|
6000-7000 |
48 |
6500 |
312000 |
|
7000-8000 |
60 |
7500 |
450000 |
|
8000-9000 |
42 |
8500 |
357000 |
|
9000-10000 |
20 |
9500 |
190000 |
|
Итого |
200 |
- |
1464000 |
Средняя арифметическая обладает рядом полезных свойств, к важнейшим из которых относятся:
1. Средняя арифметическая постоянной величины равна этой величине:
=
АприА=const;
2 . Алгебраическая сумма отклонений вариант от их средней арифметической равна нулю:
(4.13)
3. Если все варианты уменьшить (увеличить) на постоянное число А, то средняя арифметическая из них уменьшится (увеличится) на это же число:
(4.14)
4. Если все варианты увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз:
(4.14)5. Если все веса средней одинаково увеличить (уменьшить) в несколько раз, то средняя арифметическая не изменится.
(4.15)
Средняя гармоническая простая
Имеет более сложную конструкцию, чем средняя арифметическая. Используется в тех случаях, когдастатистическая информация не содержит частот по отдельнымзначениям признака, а представлена произведением значения признака начастоту. Средняя гармоническая как вид степенной средней выглядит следующим образом:
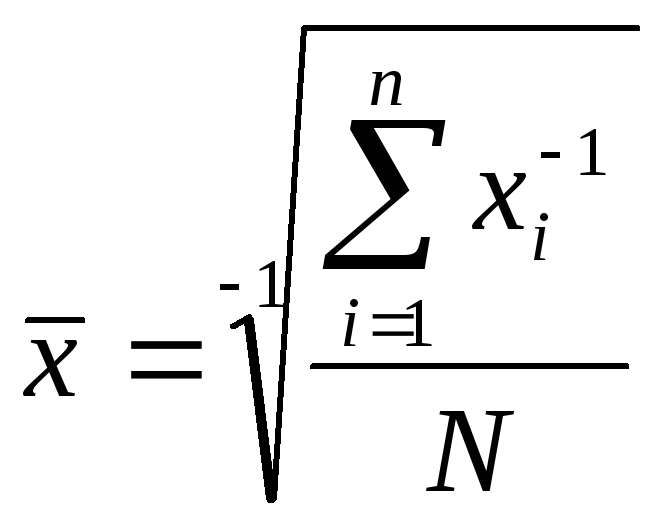(4.16)
Если исходные данные несгруппированны, то применяется средняя гармоническая простая:
(4.17)
К ней прибегают в случаях определения, например, средних затрат труда, материалов и т. д. на единицу продукции по нескольким предприятиям.
Рассмотрим пример использования средней гармонической простой:
Три предприятия производят микроволновые печи. Себестоимость их производства на 1-ом предприятии составила 4000 руб., на 2-ом - 3000 руб., на 3-ем – 5000 руб. Необходимо определить среднюю себестоимость производства микроволновой печи при условии, что на каждом предприятии общие затраты на ее изготовление составляют 600 тыс. руб.
Применять среднюю арифметическую в данном случае нельзя, так как предприятия выпускают разное количество микроволновых печей: первое – 150 шт. (600000/4000); второе – 200 шт. (600000/3000); третье – 120 шт. (600000/5000).
Среднюю себестоимость микроволновой печи можно получить, если общие затраты трех предприятий разделить на общий выпуск:
К аналогичному результату можно прийти, используя формулу средней гармонической простой:
