9. Полярная система координат

9.1. В полярной системе координат (φ,r) построить точки А(0;3); В(π/4;2); С(π/2;3); D(π;2); Е(3π/2;3).

9.2. Построить точки: А(π/2;-2); В(-π/2;3); С(-π/4;-4); D(2π/3;-3).

В номерах 9.3-9.8 записать уравнения заданных кривых в полярных координатах:

9.3. у=х.

Ответ: tgφ=1.

9.4. у=1.

Ответ: rsinφ=1.

9.5. х+у-1=0.

Ответ: .

9.6. х²+у²=а².

Ответ: r=а.

9.7. х²-у²=а².

Ответ: .

9.8. х²+у²=ах.

Ответ: r=acosφ.

В номерах 9.9-9.20 записать уравнения заданных кривых в декартовых прямоугольных координатах и построить эти кривые:

9.9. r=5.

Ответ: окружность х²+у²=25.

9.10. tgφ=-1.

Ответ: прямая у=-х.

9.11. rcosφ=2.

Ответ: прямая х=2.

9.12. rsinφ=1.

Ответ: прямая у=1.

9.13. .

Ответ: прямая х-у-1=0.

9.14. .

Ответ: прямая х+у-2=0.

9.15. r=2acosφ.

Ответ: окружность (х-а)²+у²=а².

9.16. r=2asinφ.

Ответ: окружность х²+(у-а)²=а².

9.17. sinφ=1/.

Ответ: пара лучей х=±2у, у≥0.

9.18. sinr=1/2.

Ответ: семейство концентрических окружностей радиусов r_n=(-1)ⁿ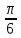+πn, n=0,1,2,…

9.19. r²sin2φ=2a².

Ответ: гипербола ху=а².

9.20. r²=a²cos2φ.

Ответ: лемниската Бернулли (х²+у²)²=а²(х²-у²).

9.21. Построить линии:

1) r=aφ (архимедова спираль); 2) r=a(1-cosφ) (кардиоида);

3) r²=a²cos2φ (лемниската); 4) r=a/φ (гиперболическая спираль);

5) r=a(1+2cosφ) (улитка Паскаля).

9.22. Написать в полярных координатах уравнение окружности с центром в точке С(0;а) и радиусом, равным а.

Ответ: .

9.23. Определить полярные координаты центра и радиус каждой из следующих окружностей:

а) r=4cosφ; б) r=3sinφ; в) r=-5sinφ; г) r=6cos;

д) r=8sin; e) r=8sin.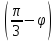

Ответ: а) С(2;0); R=2; б) С(3/2; π/2); R=3/2; в) С(5/2;-π/2); R=5/2; г) С(3;π/3); R=3; д) С(4;5π/6); R=4; е) С(4;-π/6); R=4.

9.24. Построить кривые:

1) r=3-2sin2φ; 2) r=2+cos3φ; 3) r=1-sin3φ.

Указание. Определить сначала углы, при которых имеем r_max и r_min.

Ответ: 1) r_max=5 при r_min=1 при r=3 при 2)r_max=3 при r_min=1 при 3)r_max=2 при r_min=0 при

9.25. Построить кривые: 1) r=3+2cos2φ; 2) r=3-sin3φ; 3) r=аcos2φ.

Ответ: 1) r_max=5 при r_min=1 при 2)r_max=4 при r_min=2 при 3)r=а при r=-а при r=0 при

9.26. Построить: 1) r=4(1+cosφ); 2) r=2-sinφ.

10. Поверхности

10.1. Найти центр и радиус сферы:

1) x²+y²+z²-3x+5y-4z=0; 2) x²+y²+z²=3аz

и построить изображение второй сферы.

Ответ: 1) С(1,5;-2,5;2), 2) С(0;0;а), .

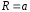10.2. Построить в левой системе координат поверхности

1) y²+z²=4; 2) y²=ах; 3) хz=4; 4) x²+y²=ax.

10.3. Написать уравнение цилиндрической поверхности с направляющей y²=4х, z=0 и с образующей, параллельной вектору {1;2;3}.

Ответ: .

10.4. Написать уравнение плоскости, проходящей через центр С поверхности x²+y²+z²-2x+y-3z=0 и перпендикулярной к прямой ОС.

Ответ: 2x-y+3z-7=0.

10.5. Написать уравнение конической поверхности с вершиной в начале координат и направляющей x²+y²=а², z=с. Построить поверхности.

Ответ: .

10.6. Написать уравнение конической поверхности с вершиной в точке А(0;-а;0) и направляющей x²=2рy, z=h. Построить изображение поверхности.

Ответ: .

10.7. Написать уравнение поверхности, образованной вращением кривой z =x², y=0: 1) вокруг оси Оz; 2) вокруг оси Ох. Построить обе поверхности.

Ответ: а) ; б).

10.8. Написать уравнение поверхности, образованной вращением эллипса =0 вокруг оси Оz.

Ответ: .

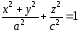10.9. Построить гиперболоид и найти его образующие, проходящие через точку (4;1;-3).

Ответ: и

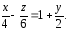
11.

11.1. Докажите, что фигура, являющаяся объединением боковой поверхности цилиндра и его нижнего основания («стакан»), гомеоморфна кругу.

11.2. Докажите, что плоскость гомеоморфна открытому кругу (т.е. кругу, к которому не причисляются точки ограничивающей его окружности), а также сфере, из которой «выколота» (удалена) одна точка.

11.3. Если фигура А состоит лишь из конечного числа точек, то через n(А) обозначим число ее точек; если же фигура А содержит бесконечно много точек, то условимся писать n(А)=∞. Является ли n(А) топологическим инвариантом?

11.4. Фигура А называется вложимой в плоскость, если она гомеоморфна некоторой фигуре, лежащей в плоскости. Например, «стакан» (задача 8) вложим в плоскость. Является ли свойство фигуры быть вложимой в плоскость топологическим инвариантом?

11.5. Докажите, что всякая простая замкнутая линия на сфере разбивает сферу на две области.

11.6. На плоскости проведены k ломаных линий, каждая из которых соединяет две заданные точки p и q. Докажите, что если других общих точек ломаные попарно не имеют, то плоскость разбита на k областей.

11.7. В шаре высверлены три сквозных цилиндрических отверстия, оси которых проходят через центр шара. Докажите, что поверхность получившегося тела, гомеоморфна сфере с пятью ручками.

11.8. На поверхности P_kпроведеноqконтуров, не пересекающихся друг с другом, причем после разрезания по всем этим контурам поверхность остается связной. Докажите, что q≤k.

11.9. На замкнутой поверхности Q осуществлено топологически правильное разбиение: каждая грань – пятиугольник, в каждой вершине сходятся по четыре грани. Докажите, что если число граней не кратно восьми, то поверхность Q не ориентируема.

11.10. На замкнутой поверхности Q проведены три линии p,q,r, гомеоморфные отрезку, которые имеют общие концы и попарно не имеют других общих точек. Докажите, что если разрез по одной из линий составляет поверхность связной, то хотя бы одна из двух других также обладает этим свойством.

11.11. На сфере вырезаны m+n+p дыр; m из них заклеены ручками, а n– лентами Мебиуса. Докажите, что эйлерова характеристика получившейся поверхности с краем равна 2-2m-n-p.