7. Плоскость и прямая в пространстве

7.1. Построить плоскости: 1) 5х-2у+3z-10=0; 2) 3х+2у-z=0; 3) 3х+2z=6; 4) 2z-7=0.

7.2. Заданы плоскость Р и точка М. Написать уравнение плоскости P', проходящей через точку М параллельно плоскости Р, и вычислить расстояние (P,P'), если:

а) Р: -2х+у-z+1=0, М(1;1;1);

б) Р: х-у-1=0, М(1;1;2).

Ответ: а) 2х-у+z-2=0; 1/; б)х-у=0, плоскость параллельна оси Оz и проходит через начало координат; 1/.

7.3. Найти плоскость, проходящую через точку (2;2;-2) и параллельную плоскости х-2у-3z=0.

Ответ: х-2у-3z=4.

7.4. Написать уравнение плоскости, проходящей через точку М₀(-2;7;3) параллельно плоскости х-4у+5z+1=0.

Ответ: х-4у+5z+15=0.

7.5. Написать уравнение плоскости, проходящей через точку М₀(2;3;-4) параллельно плоскости YOZ.

Ответ: х-2=0.

7.6. Написать уравнение плоскости, проходящей через точку М₀(-2;1;4) параллельно плоскости 3х+2у-7z+8=0.

Ответ: 3х+2у-7z+32=0.

7.7. Написать уравнение плоскости P', проходящей через заданные точки М₁ и М₂ перпендикулярно заданной плоскости Р, если:

а) Р: -х+у-1=0, М₁(1;2;0), М₂(2;1;1);

б) Р: 2х-у+z+1=0, М₁(0;1;1), М₂(2;0;1).

Ответ: а) х+у-3=0; б) х+2у-2=0.

7.8. Даны точки М₁(0;-1;3) и М₂(1;3;5). Написать уравнение плоскости, проходящей через точку М₁ и перпендикулярной к вектору =.

Ответ: х+4у-2z=2.

7.9. Написать уравнение плоскости, проходящей через точку М(-1;2;3) перпендикулярно вектору .

Ответ: х-2у-3z+14=0.

7.10. Написать уравнение плоскости, проходящей через точку (-1;-1;2) и перпендикулярной к плоскостям х-2у+z-4=0 и x+2у-2z+4=0.

Ответ: 2х+3у+4z=3.

7.11. Написать уравнение плоскости, проходящей через точки М₁(2;3;-1), М₂(1;5;3) перпендикулярно плоскости 3х-у+3z+15=0.

Ответ: 2х+3у-z-14=0.

7.12. Составить уравнение плоскости, проходящей через точку А(1;1;-1) и перпендикулярной к плоскостям 2х-у+5z+3=0 и х+3у-z-7=0

Ответ: 2х-у-z-2=0.

7.13. Написать уравнение плоскости, проходящей через точку (0;0;а) и перпендикулярной к плоскостям х-у-z=0 и 2у=х.

Ответ: 2х+у+z=а.

7.14. Даны точки М₁(0;-1;3), М₂(1;3;5). Написать уравнение плоскости, проходящей через точку М₁ перпендикулярно вектору .

Ответ: х+4у+2z-2=0.

7.15. Написать уравнение плоскости, проходящей через точки (0;-5;0) и (0;0;2) перпендикулярно плоскости х+5у+2z-10=0.

Ответ: 2у-5z+10=0.

7.16. Написать уравнение плоскости, проходящей через точку М₀(-2;3;6) перпендикулярно плоскостям 2х+3у-2z-4=0, 3х+5у+z=0.

Ответ: 13х-8у+z+44=0.

7.17. Написать уравнение плоскости, проходящей через точку М параллельно векторам и, если:

а) М(1;1;1), (0;1;2),(-1;0;1);

б) М(0;1;2), (2;0;1),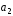(1;1;0).

Ответ: а) х-2у-z=0; б) -х+у+2z-5=0.

7.18. Написать уравнение плоскости, проходящей через точку М₀(2;-3;1) параллельно векторам .

Ответ: х+у-z+2=0.

7.19. Написать уравнение плоскости, проходящей через точки М₁ и М₂, параллельно вектору , если:

а) М₁(1;2;0), М₂(2;1;1), (3;0;1);

б) М₁(1;1;1), М₂(2;3;-1), (0;-1;2).

Ответ: а) –х+2у-3z-3=0; б) 2х-2у-z+1=0.

7.20. Написать уравнение плоскости, проходящей через три заданные точки М₁, М₂ и М₃, если:

а) М₁(1;2;0), М₂(2;1;1), М₃(3;0;1);

б) М₁(1;1;1), М₂(0;-1;2), М₃(2;3;-1).

Ответ: а) х+у-3=0; б) 2х-у-1=0.

7.21. Написать уравнение плоскости, проходящей через точки М₁(1;-1;2), М₂(2;1;2) и М₃(1;1;4).

Ответ: 2х-у+z=5.

7.22. Написать уравнение плоскости, проходящей через точки М₁(3;-1;2), М₂(4;-1;-1), М₃(2;0;2) .

Ответ: 3х+3у+z-8=0.

7.23. Написать уравнение плоскости, проходящей через три точки М₁(1;-1;0), М₂(2;1;-3), М₃(-1;0;1) .

Ответ: х+у+z=0.

В задачах 7.24-7.27. исследовать взаимное расположение заданных плоскостей. При этом в случае, если плоскости параллельны, то найти расстояние (P₁,P₂) между плоскостями, а в случае, если плоскости пересекаются – косинус угла между ними.

7.24. Р₁: -х+2у-z+1=0, Р₂: у+3z-1=0.

Ответ: Пересекаются, cos.

7.25. Р₁: 2х-у+z-1=0, Р₂: -4х+2у-2z-1=0.

Ответ: параллельны, (Р₁,Р₂)=.

7.26. Р₁: х-у+1=0, Р₂: у-z+1=0.

Ответ: Пересекаются, cos.

7.27. Р₁: 2х-у-z+1=0, Р₂: -4х+2у+2z-2=0.

Ответ: Совпадают.

7.28. Найти расстояние от точки (5;1;-1) до плоскости x-2у-2z+4=0.

Ответ: 3.

7.29. Найти расстояние от точки (4;3;0) до плоскости, проходящей через точки М₁(1;3;0), М₂(4;-1;2) и М₃(3;0;1).

Ответ:

7.30. Найти расстояние от точки М₁(2;-1;-1) до плоскости 16х-12у+15z-4=0.

Ответ:1.

7.31. Найти расстояние от точки М₀(1;3;-2) до плоскости 2х-3у-4z+12=0.

Ответ: .

7.32. Найти угол между плоскостями:

1) х-2у+2z-8=0 и x+z-6=0; 2) х+2z-6=0 и x+2y-4=0.

Ответ: 1) 45˚; 2) .

7.33. Найти угол между плоскостями х+у-1=0 и 2х-у+z+1=0.

Ответ: .

7.34. Найти угол между плоскостями х+2у-3z+4=0, 2х+3у+z+8=0.

Ответ: .

7.35. Написать уравнение плоскости, проходящей через точку М₀(1;7;-5) и отсекающей от осей координат положительные и равные отрезки.

Ответ: x+y+z-3=0.

7.36. Написать уравнение плоскости, проходящей через точку М₁(-4;0;4) и отсекающей на осях Ох и Оу отрезки а=4 и b=3.

Ответ: .

7.37. Вычислить объем пирамиды, ограниченной плоскостью Р: 2х-3у+6z-12=0 и координатными плоскостями.

Ответ: 8.

7.38. Написать каноническое уравнение прямой, проходящей через точку М₀(2;0;-3) параллельно:

а) вектору (2;-3;5);

б) прямой ;

в) оси Ох;

г) оси Оz;

д) прямой

е) прямой х=-2+t, y=2t, z=1-1/2t.

Ответ: а) ; б); в);

г) ; д); е).

7.39. Написать уравнение прямой, проходящей через точку А(4;3;0) и параллельной вектору {-1;1;1}. Найти след прямой на плоскостиуОz и построить прямую.

Ответ: .

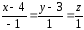7.40. Написать уравнения прямой, проходящей через точку А(0;-4;0) и параллельной вектору {1;2;3}, найти след прямой на плоскостихОz и построить прямую.

Ответ: .

7.41. Написать уравнения прямой, проходящей через точку М₀(2;-3;-4) параллельно прямой: .

Ответ: .

7.42. Написать уравнения прямой, проходящей через точку (-4;3;0) параллельно прямой .

Ответ: .

7.43. Написать уравнения прямой, проходящей через две заданные точки М₁ и М₂, если:

а) М₁(1;-2;1), М₂(3;1;-1);

б) М₁(3;-1;0), М₂(1;0;-3).

Ответ: а) 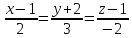; б).

7.44. Построить прямую, проходящую через точки А(2;-1;3) и В(2;3;3), и написать ее уравнения.

Ответ: х=2, z=3.

7.45. Написать уравнения прямой, проходящей через точки А(-1;2;3) и В(2;6;-2). Найти ее направляющие косинусы.

Ответ:

.

7.46. Написать канонические уравнения прямой, образующей с осями координат углы и проходящей через точкуМ₀(-1;0;5).

Ответ: .

7.47. Найти угол между прямыми: x-y+z-4=0, 2x+y-2z+5=0 и x+y+z-4=0, 2x+3y-z-6=0.

Ответ:

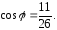
7.48. Найти угол между прямыми 2x-y-7=0, 2x-z+5=0 и 3x-2y+8=0, z=3х.

Ответ: Приведем уравнения к канонической форме: и;

7.49. Найти угол между прямыми:

и .

Ответ: /3.

7.50. Найти угол между прямыми и .

Ответ: .

7.51. Доказать, что прямые и параллельны.

7.52. Написать канонические уравнения перпендикуляра, опущенного из начала координат на плоскость 4х-у+2z-3=0.

Ответ: .

7.53. Написать уравнения прямой, проходящей через точку М₀(2;1;-1) перпендикулярно плоскости х-у+z+1=0.

Ответ: .

7.54. При каком значении  плоскость 5х-3у+z+1=0 будет параллельна прямой

Ответ: -11.

7.55. Показать, что прямая параллельна плоскости 2x+y-z=0, а прямая лежит в этой плоскости.

Ответ: Для обеих прямых но точка первой (-1;-1;3) не лежит на плоскости, а точка второй (-1;-1;-3) лежит на плоскости.

7.56. Написать уравнение плоскости, проходящей через точку М₀(2;2;-2) перпендикулярно линии пересечения плоскостей 3х-2у-z+1=0 и х-у-z=0.

Ответ: х+2у-z-8=0.

7.57. Написать уравнение плоскости, проходящей через ось ОZ и точку М₀(1;-2;1).

Ответ: 2х+у=0.

7.58. Найти уравнение плоскости, проходящей через точку М₀(1;-2;3) и прямую: .

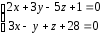Ответ: 7х+5у-9z+30=0.

7.59. Написать уравнение плоскости, проходящей через прямую и точку (3;4;0).

Ответ: х-2у+z+5=0.

7.60. Найти уравнение плоскости, проходящей через прямую перпендикулярно плоскости 3х+3у-z+1=0.

Ответ: 6х-5у+3z-11=0.

7.61. Написать уравнение плоскости, проходящей через прямую перпендикулярно плоскости 2х+3у-z=4.

Ответ: 8х-5у+z-11=0.

7.62. Написать уравнение плоскости, проходящей через параллельные прямые 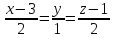и.

Ответ: x+2y-2z=1.

7.63. Написать уравнение плоскости, проходящей через параллельные прямые и .

Ответ: х-у-z=0.

7.64. Написать уравнение плоскости, проходящей через пару параллельных прямых и .

Ответ: 3х-2у-3=0.

7.65. Написать уравнение плоскости, проходящей через прямые и .

Ответ: х+2у-2z=1.

7.66. Найти точку пересечения с плоскостью 2х+3у-2z+2=0.

Ответ: (3;2;7).

7.67. Составить уравнения прямой, проходящей через точки пересечения плоскости х-3у+2z+1=0 с прямыми

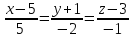и .

Ответ: .

7.68. Найти уравнения проекции прямой на плоскостьх-3у-z+8=0.

Ответ: .

7.69. Найти проекцию точки (3;1;-1) на плоскость x+2y+3z-30=0.

Ответ: (5;5;5).

7.70. Найти проекцию точки (3;1;-1) на плоскость 3x+y+z-20=0.

Ответ: (6;2;0).

7.71. Найти проекцию точки (2;3;4) на прямую x=y=z.

Ответ: (3;3;3).

7.72. Найти проекцию точки (1;2;8) на прямую .

Ответ: (3;-1;1).

7.73. Найти угол прямой y=3x-1, 2z=-3х+2 с плоскостью 2x+y+z-4=0.

Ответ: .

7.74. Найти угол между прямой и плоскостью 6х-3у+2z=0.

Ответ: .

7.75. Заданы прямая L: и точкаМ(0;1;2)L (проверить!). Требуется:

а) написать уравнение плоскости, проходящей через прямую L и точку М;

б) написать уравнение плоскости, проходящей через точку М перпендикулярно прямой L;

в) написать уравнение перпендикуляра, опущенного из точки М на прямую L;

г) вычислить расстояние (M,L);

д) найти проекцию точки М на прямой L.

Ответ: а) х-2у+z=0; б) 2х+у-1=0; в) или; г) 18/; д)M'(3/5;-1/5;-1).

7.76. Найти расстояние между параллельными прямыми

и .

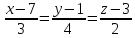Ответ: 3.

7.77. Найти расстояние от точки А(2;3;-1) до заданной прямой L:

а) б)

Ответ: а) 6/; б) 21.

7.78. Найти расстояние от точки М(2;-1;3) до прямой .

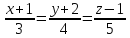Ответ: .

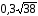7.79. Найти расстояние от точки М(3;0;4) до прямой y=2x+1, z=2х.

Ответ: А(0;1;0), .

7.80. Найти расстояние между прямыми и .

Ответ: .