
- •Геометрия и топология
- •I курса очной формы обучения
- •Предисловие
- •1. Линейные операции над векторами
- •2. Прямоугольные координаты точки и вектора. Базис
- •3. Скалярное произведение векторов
- •4. Векторное произведение векторов
- •5. Смешанное произведение векторов
- •6. Прямая на плоскости
- •7. Плоскость и прямая в пространстве
- •8. Кривые второго порядка
- •9. Полярная система координат
- •10. Поверхности
- •Список рекомендуемой литературы
5. Смешанное произведение векторов
5.1.
Векторы
 ,
, ,
, образуют правую тройку, взаимно
перпендикулярны и |
образуют правую тройку, взаимно
перпендикулярны и | |=4,
|
|=4,
| |=2,
|
|=2,
| |=3.
Вычислить
|=3.
Вычислить

 .
.
Ответ: 24.
5.2.
Векторы
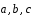 образуют
левую тройку, |
образуют
левую тройку, | |=1,
|
|=1,
| |=2,
|
|=2,
|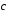 |=3
и
|=3
и °;
°;

 ,
,


 .
Найти
.
Найти


 .
.
Ответ: -3/2.
5.3.
Заданы векторы
 (1;-1;3),
(1;-1;3), (-2;2;1),
(-2;2;1), (3;-2;5).
Вычислить
(3;-2;5).
Вычислить

 .
Какова ориентация троек: а) (
.
Какова ориентация троек: а) (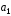 ,
, ,
, ),
б) (
),
б) ( ,
, ,
, ),
в) (
),
в) ( ,
, ,
, )?
)?
Ответ: -7. а) левая; б) правая; в) правая.
5.4.
Установить, образуют ли векторы
 ,
, и
и базис
в множестве всех векторов, если:
базис
в множестве всех векторов, если:
а)
 (2;3;-1),
(2;3;-1), (1;-1;3),
(1;-1;3), (1;9;-11);
б)
(1;9;-11);
б) (3;-2;1),
(3;-2;1), (2;1;2),
(2;1;2), (3;-1;-2).
(3;-1;-2).
Ответ: а) нет; б) да.
5.5. Проверить, компланарны ли данные векторы:
а)
 ,
,
 ,
, ;
;
б)
 ,
,
 ,
, .
.
Ответ: а) да; б) нет.
5.6.
Доказать, что векторы


 компланарны.
Ответ:
компланарны.
Ответ:

5.7.
Проверить компланарность векторов


 .
.
Ответ: компланарны.
5.8.
При каком
векторы
 будут компланарны?
будут компланарны?
а)
 (;3;1),
(;3;1),
 (5;-1;2),
(5;-1;2), (-1;5;4);
б)
(-1;5;4);
б) (1;2;1),
(1;2;1),
 (1;;0),
(1;;0),
 (0;;1).
(0;;1).
Ответ: а) -3; б) при любом .
5.9. Доказать, что четыре точки А(1,2,-1), В(0;1;5), С(-1;2;1) и D(2;1;3) лежат в одной плоскости.
5.10. Проверить, лежат ли точки А(2;-1;-2); В(1;2;1); С(2;3;0); D(5;0;6) в одной плоскости.
Ответ: не лежат.
5.11.
Построить параллелепипед на векторах
 ,
,
 ,
, и вычислить его объем. Правой или левой
будет связка векторов
и вычислить его объем. Правой или левой
будет связка векторов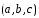 ?
?
Ответ: V=51, левая.
5.12.
Найти объем параллелепипеда, построенного
на векторах


 .
.
Ответ: 51.
5.13. Построить пирамиду с вершинами О(0;0;0), А(5;2;0), В(2;5;0) и С(1;2;4) и вычислить ее объем, площадь грани АВС и высоту пирамиды, опущенную на эту грань.
Ответ:
V=14,

5.14.
Вычислить
объем тетраэдра ОАВС,
если
 ;
; ;
; .
.
Ответ: 17/2.
5.15. Вычислить объем тетраэдра с вершинами в точках А(2;-3;5); В(0;2;1), С(-2;-2;3) и D(3;2;4).
Ответ: 6.
5.16.
В тетраэдре с вершинами в точках А(1;1;1),
В(2;0;2),
С(2;2;2)
и D(3;4;-3)
вычислить высоту h=| |.
|.
Ответ:
3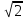 .
.
5.17. Задана пирамида с координатами своих вершин: А(2;0;0); В(0;3;0); С(0;0;6) и D(2;3;8). Вычислить ее объем и высоту, опущенную на грань АВС.
Ответ:
14;
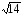 .
.
6. Прямая на плоскости
В задачах 6.1-6.3 требуется:
написать уравнение прямой, привести его к общему виду и построить прямую;
привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
6.1.
Прямая L
задана точкой М0(х0,
у0)L
и нормальным вектором
 (A,B):
(A,B):
а)
М0(-1;2),
 (2;2);
б)М0(2;1),
(2;2);
б)М0(2;1),
 (2;0);
в)М0(1;1),
(2;0);
в)М0(1;1),
 (2;-1).
(2;-1).
Ответ:
а) 2(х+1)+2(у-2)=0.
Общее уравнение: х+у-1=0.
Нормальное уравнение:
 б) 2(х-2)=0.
Общее уравнение: х-2=0,
прямая параллельна оси Оу.
Нормальное уравнение: х-2=0;
р=2;
в) 2(х-1)-(у-1)=0.
Общее уравнение: 2х-у-1=0.
Нормальное уравнение:
б) 2(х-2)=0.
Общее уравнение: х-2=0,
прямая параллельна оси Оу.
Нормальное уравнение: х-2=0;
р=2;
в) 2(х-1)-(у-1)=0.
Общее уравнение: 2х-у-1=0.
Нормальное уравнение:
 .
.
6.2.
Прямая L
задана точкой М0(х0,
у0)L
и направляющим вектором
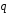 (l,m):
(l,m):
а)
М0(-1;2),
 (3;-1);
б)М0(1;1),
(3;-1);
б)М0(1;1),
 (0;-1);
в)М0(-1;1),
(0;-1);
в)М0(-1;1),
 (2;0).
(2;0).
Ответ:
а)
 .
Общее уравнение:х+3у-5=0.
Нормальное уравнение:
.
Общее уравнение:х+3у-5=0.
Нормальное уравнение:
 б)
б) Общее уравнение: -х+1=0,
прямая параллельна оси Оу.
Нормальное уравнение: х-1=0;
р=1;
в)
Общее уравнение: -х+1=0,
прямая параллельна оси Оу.
Нормальное уравнение: х-1=0;
р=1;
в)
 .
Общее уравнение:у-1=0,
прямая параллельна оси Ох.
Нормальное уравнение: у-1=0;
р=1.
.
Общее уравнение:у-1=0,
прямая параллельна оси Ох.
Нормальное уравнение: у-1=0;
р=1.
6.3. Прямая L задана точками М1(х1,у1) и М2(х2, у2):
а) М1(1;2), М2(-1;0); б) М1(1;1), М2(1;-2); в) М1(2;2), М2(0;2).
Ответ:
а)
 .
Общее уравнение:х-у+1=0.
Нормальное уравнение:
.
Общее уравнение:х-у+1=0.
Нормальное уравнение:
 б)
б) .
Общее уравнение:х-1=0,
прямая параллельна оси Оу.
Нормальное уравнение х-1=0;
р=1.
в)
.
Общее уравнение:х-1=0,
прямая параллельна оси Оу.
Нормальное уравнение х-1=0;
р=1.
в)
 .
Общее уравнение:у-2=0,
прямая параллельна оси Ох.
Нормальное уравнение: у-2=0;
р=2.
.
Общее уравнение:у-2=0,
прямая параллельна оси Ох.
Нормальное уравнение: у-2=0;
р=2.
6.4. Построить прямую, отсекающую на оси Оу отрезок b=3 и составляющую с осью Ох угол: 1) 45˚; 2) 135˚. Написать уравнения этих прямых.
Ответ:
1)
 2)
2) .
.
6.5.
Определить параметры k
и
b
для
каждой из прямых: 1) 2х-3у=6;
2) 2х+3у=0;
3) у=-3;
4)
 .
.
Ответ:
1)
 2)
2) 3)
3) 4)
4)
6.6. Уравнения прямых: 1) 2х-3у=6; 2) 3х-4у+4=0 привести к виду в отрезках на осях.
Ответ:
1)
 2)
2)
6.7. Заданы прямая L и точка М. Требуется:
1) вычислить расстояние ρ(M,L) от точки М до прямой L;
2) написать уравнение прямой L', проходящей через точку М перпендикулярно заданной прямой L;
3) написать уравнение прямой L", проходящей через точку М параллельно заданной прямой L.
Исходные данные:
а) L: -2x+y-1=0, M(-1;2); б) L: 2y+1=0, M(1;0); в) L: х+y+1=0, M(0;-1).
Ответ:
а) (М,L)= -2(x+1)+(y-2)=0;
-2(x+1)+(y-2)=0;
б)
(М,L)= 2y=0;
2y=0;
в)
(М,L)=0 x+y+1=0.
x+y+1=0.
6.8. Найти расстояния от точек А(4;3), В(2;1) и С(1;0) до прямой 3х+4у-10=0. Построить точки и прямую.
Ответ: 2,8; 0; 1,4.
В
задачах 6.9-6.13
исследовать взаимное расположение
заданных прямых L1
и
L2.
При этом в случае, если прямые параллельны,
то найти расстояние (L1,L2)
между прямыми, а в случае, если прямые
пересекаются – косинус угла ( )
и точкуМ0
пересечения прямых.
)
и точкуМ0
пересечения прямых.
6.9. L1: -2x+y-1=0, L2: 2y+1=0.
Ответ:
пересекаются в точке М0(-3/4;-1/2);
cos( )=1/
)=1/ .
.
6.10.

Ответ:
пересекаются в точке М0(1;0);
cos( )=2/
)=2/ .
.
6.11. L1: x+y-1=0, L2: 2х-2y+1=0.
Ответ:
Параллельны; (L1,L2)= /4.
/4.
6.12.
L1:
x+y-1=0,

Ответ:
Параллельны; (L1,L2)= .
.
6.13. L1: -x+2y+1=0, L2: 2х-4y-2=0.
Ответ: совпадают.
6.14. Среди прямых 3х-2у+7=0, 6х-4у-9=0, 6х+4у-5=0, 2х+3у-6=0 указать параллельные и перпендикулярные.
6.15. Определить угол между прямыми:
1)
у=2х-3,
у=
 +1;
2) 5х-у+7=0,
2х-3у+1=0.
+1;
2) 5х-у+7=0,
2х-3у+1=0.
Ответ:
1)
 2) 45˚.
2) 45˚.
6.16. Показать, что прямые 2х-3у=6 и 4х-6у=25 параллельны, и найти расстояние между ними.
Указание. На одной из прямых взять произвольную точку и найти расстояние от нее до другой прямой.
Ответ:
 .
.
6.17. Построить области, координаты точек которых удовлетворяют неравенствам:
1) y<2-x, x>-2, y>-2;
2) y>2-x, x<4, y<0;
3)
 ,y≥x+2,
x≥-4.
,y≥x+2,
x≥-4.
6.18. Написать уравнения сторон ромба с диагоналями 10 см и 6 см, приняв бόльшую диагональ за ось Ох и меньшую – за ось Оу.
Ответ:

6.19. Написать уравнение прямой, проходящей через точку А(4;3) и отсекающей от координатного угла треугольник площадью, равной 3.
Ответ:
 или
или .
.
6.20. Составить уравнение прямой, которая проходит через точку М(8;6) и отсекает от координатного угла треугольник с площадью, равной 12.
Ответ: 3х-2у-12=0, 3х-8у+24=0.
6.21. Написать уравнение прямой, проходящей через точку М0(2;4) и отстоящей от точки А(0;3) на расстояние =1.
Ответ: х+1=0, у-2=0.
6.22 Найти уравнения прямых, параллельных прямой 12х+5у-7=0 и отстоящих от нее на расстоянии d=3.
Ответ: 12х+5у-46=0, 12х+5у+32=0.
6.23. Написать уравнение прямой, проходящей через точку М0(1;2) и удаленной от точки А(-2;-5) вдвое дальше, чем от точки В(1;8).
Ответ: 13х+у-11=0, 15х-у-13=0.
6.24. Написать уравнение прямой, проходящей через точку М0(-2;3) на одинаковых расстояниях от точек М1(5;-1) и М2(3;7).
Ответ: 4х+у+5=0 или у-3=0.
6.25.
Написать уравнение прямой, проходящей
на расстоянии
 от точкиА(5;4)
перпендикулярно прямой 2х+6у-3=0.
от точкиА(5;4)
перпендикулярно прямой 2х+6у-3=0.
Ответ: 3х-у-1=0, 3х-у-21=0.
6.26. Найти точку В, симметричную точке А(-2;4) относительно прямой 3х+у-8=0.
Ответ: (4;6).
6.27. В треугольнике с вершинами А(-2;0), В(2;6) и С(4;2) проведены высота ВD и медиана ВЕ. Написать уравнения стороны АС, медианы ВЕ и высоты ВD.
Ответ:

6.28. Дан треугольник с вершинами А(-2;0), В(2;4) и С(4;0). Написать уравнения сторон треугольника, медианы АЕ, высоты АD и найти длину медианы АЕ.
Ответ:
АЕ:
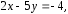 AD:
AD:


6.29. Найти длину высоты BD в треугольнике с вершинами А(-3;0), В(2;5) и С(3;2).
Ответ:

6.30. Написать уравнения сторон треугольника АВС, если задана его вершина А(1;3) и уравнения двух медиан x-2y+1=0 и y-1=0.
Ответ: х+2у-7=0, х-4у-1=0, х-у+2=0.
6.31. Написать уравнения сторон треугольника, зная одну его вершину В(2;6), а также уравнения высоты x-7y+15=0 и биссектрисы 7x+y+5=0, проведенных из одной вершины.
Ответ: 4х-3у+10=0, 7х+у-20=0, 3х+4у-5=0.
6.32. Даны две противоположные вершины квадрата А(1;3) и С(-1;1). Найти координаты двух его других вершин и написать уравнения его сторон.
Ответ: В(1;1); D(-1;3); (АВ): х-1=0; (ВС): у-1=0; (CD): х+1=0;
(АD): у-3=0.
6.33. Известны уравнение одной из сторон квадрата x+3y-3=0 и точка пересечения диагоналей N(-2;0). Написать уравнения остальных его сторон.
Ответ: 3х-у+1=0, х+3у+7=0, 3х-у+11=0.
6.34. Из точки М(5;4) выходит луч света под углом φ=arctg2 к оси Ох и отражается от нее. Написать уравнения падающего и отраженного лучей.
Ответ: у-2х+6=0, у+2х-6=0.
