«УТВЕРЖДАЮ»
Ректор университета
_______________ О.Н. Федонин
«_____»___________ 2014г.
Геометрия и топология
Методические указания и задачи
к практическим занятиям для студентов
I курса очной формы обучения
инженерно-технических специальностей
(I семестр)
Брянск 2014
УДК 511
Геометрия и топология [Текст]+[Электронный ресурс]: Методические указания и задачи к практическим занятиям для студентов I курса очной формы обучения инженерно-технических специальностей (I семестр). – Брянск: БГТУ. - с.
Разработали: ст.пр. Кобзев В.М.
доц. Сычева Н.В.
Рекомендовано кафедрой «Высшая математика»
(протокол № от . . ).
Научный редактор Гореленков А.И.
Редактор издательства Афонина Л.И.
Компьютерный набор Левкина А.П.
Темплан 2014 г., п.
Подписано в печать Формат 60х84 1/16 Бумага офсетная
Офсетная печать. Печ. Л. Уч.-изд. Л. Т. 30 экз. Заказ Бесплатно
Издательство Брянского государственного технического университета
Брянск, бульвар 50-летия Октября, 7, тел. 588-249
Лаборатория оперативной печати БГТУ, ул. Институтская, 16
Предисловие
В наши дни в естествознании инженерных науках и их всевозможных приложениях все большую роль играют математические методы исследования и проектирования. Это обусловлено ускоренным развитием компьютерных технологий, благодаря которым существенно расширяются возможности успешного применения математики при решении конкурсных общетеоретических и прикладных задач.
Немаловажную роль в их решении играют геометрические методы, поскольку зачастую именно в геометрических идеях и образах заложены выдающиеся идеи современных математических открытий.
1. Линейные операции над векторами
1.3.
На трех компланарных векторах
,
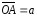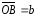и
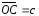построен параллелепипед. Указать те
вектор-диагонали, которые соответственно
равны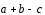
,
,
,
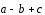и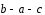
.
1.4.
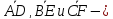медианы треугольника АВС.
Доказать равенство
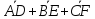=0.
1.5.
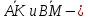медианы
треугольника АВС.
Выразить через
=
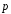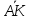и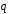
=
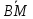векторы
.
Ответ:
;
;
=
.
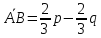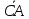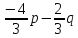1.6.
В параллелограмме ABCD
обозначены:
=
,
=
.
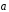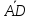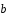Выразить через
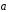и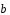
векторы
,
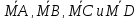где М – точка пересечения диагоналей
параллелограмма.
Ответ:
;
;
;
.
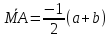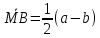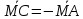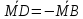1.7.
В
треугольнике АВС
.
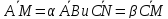Полагая,
=
,
=
,
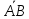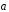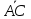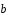выразить
через векторы
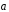и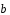
.
Ответ:
;
.
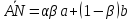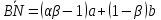1.8.
ABCDEF
– правильный шестиугольник, причем
=
,
=
.
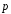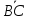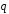Выразить через
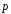и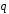
векторы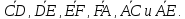
Ответ:
;
.
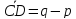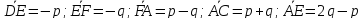1.9.
М
– точка пересечения медиан треугольника
АВС,
О
– произвольная точка пространства.
Доказать равенство
.
1.10.
В
пространстве заданы треугольники АВС
и A'B'C';
M
и M'
–точки пересечения их медиан. Выразить
вектор
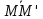через векторы
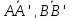и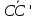
.
Ответ:
).
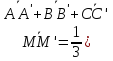1.11.
Точки Е
и F
– середины сторон AD
и BC
четырехугольника АВСD.
Доказать, что
.
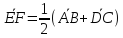Ввести отсюда теорему о средней линии
трапеции.
1.12.
В трапеции ABCD
отношение длины основания AD
к длине основания BC
равно .
Полагая
=
,
=
,
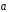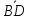выразить через
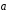и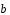
векторы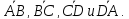
Ответ:
.
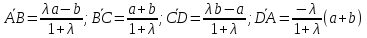1.13.
В равнобедренной трапеции ОАСВ
угол ВОА=60˚,
ОВ=ВС=СА=2,
М
и N
– середины сторон ВС
и АС.
Выразить векторы
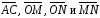
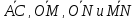
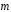и
–
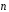единичные векторы направлени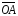й
и
.
Ответ:
,
,
,
.
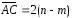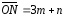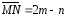1.14.
На
стороне [AD]
параллелограмма АВСD
отложен вектор
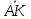длины |
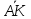|=1/5|
|,
а на диагонали [AC]
– вектор
длины |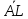
|=1/6|
|.
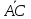Доказать, что векторы
коллинеарны и найти
такое, что
.
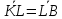Ответ: =5.
1.15.
Разложить
вектор
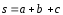по
трем некомпланарным векторам:
,
,
.
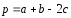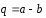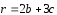Ответ:
s=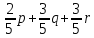
.
1.16.
Найти
линейную зависимость между данными
четырьмя некомпланарными векторами:
,
,
,
.
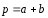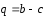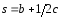Ответ: 3p-4q-3r-2s=0.
1.17.
Даны
четыре вектора
.
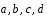Вычислить их сумму, если известно, что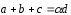
,
и векторы
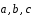некомпланарны.
Ответ: 0
1.18.
Даны три некомпланарных вектора
.
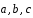Доказать, что векторы
,
,
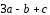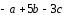компланарны.
1.19.
Даны три некомпланарных вектора
.
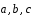Вычислить значения
при которых векторы
,
,
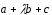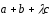компланарны.
Ответ: 0,1,2.
1.20.
Даны
три некомпланарных вектора
.
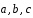Вычислить значения
и µ при которых векторы
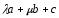и
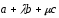коллинеарны.
Ответ: =µ=1.