Часть 1.
1. Что называется объединением, пересечением, разностью, симметрической разностью множеств, дополнением множества?
2. Что такое инъективное, сюръективное, биективное отображение? (с примерами)
Что вы знаете о мощности множеств двоичных наборов и о мощности множества всех подмножеств данного множества?
4. Что такое правило произведения? (с примером)
5. Что такое перестановки и что вы знаете о числе перестановок? (с примерами)
6. Что такое размещение и что вы знаете о числе размещений? (с примером)
7. Что такое сочетания и что вы знаете о числе сочетаний? (с примером)
8. Что такое перестановки и что вы знаете об их числе? {с примером)
9. Что такое рефлексивное, симметричное, транзитивное отношение, отношение эквивалентности и каково его основное свойство?
МО.
11. Что такое отношение строгого порядка, нестрогого порядка?
12. В чем состоит числовое сравнение двоичных наборов и как сравнить двоичные наборы по Парето?
1.
-
Объединение - такое мн-во, элементами которого явл все элементы множества А и В
-
Пересечение - такое мн-во, элементы которого одновременно * входят в А и в В
-
Разность А и В - такое мн-во, элементы которого принадлежат А, но не принадлежат В
-
Симметрическая разность - такое мн-во, в которое входят только
элементы мн-ва А и только элементы мн-ва B
-
Дополнение мн-ва - разность универсального и заданного мн-ва
2.
Отображение называют инъективным, если различные элементы мн-ва А переходят в различные элементы мн-ва В.
-
Отображение называют сюръективным. если каждый элемент мн-ва В имеет свой прообраз в мн-ве А.
-
Отображение биективно, когда оно инъективно и сюръективно.
3.
Мн-во
всех двоичных
наборов
длины п обозначается Bin.
Для любого n - card
=
.
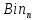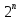Мн-во
всех подмн-в данного мн-ва А обозначается
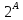
card
=
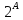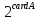
4.
Декартовым произведением мн-в А и В называется мн-во всех пар (а, Ь), где а прин А, b прин В. обозн АхВ.
5.
Перестановка - упорядоченный набор чисел (1,2,...,п), обычно трактуемый как биекция на множестве {1,2,п}, которая числу i ставит в соответствие i-й элемент из набора, п различных предметов можно переставить п! различными
способами.
Рп = п!
6.
Пусть имеется п различных предметов, из которых нужно выбрать клетук, причем порядок выбора существенен.
=
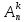способов
размещения.
7.
Пусть из n различных предметов нужно выбрать к штук, но
порядок выбора НЕ существенен.
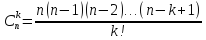способов
сочетания
8.
Иногда
среди переставляемых предметов есть
одинаковые. Пусть имеется kl одинаковых
предметов 1-го типа, к2 предметов 2-го
типа ...
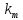предметов
m-готипа, а всего n=kl+k2+...+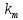
предметов.
=
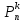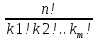
9.
Всякое подмн-во Г декартова произведения АхА называется отношением на мн-ве А.
т.е. Г -это мн-во некоторых пар, находящихся в данном отношении, обозн аГЬ
-
Отношение называется рефлексивным, если аГа для всех а прин А. т.е. каждый элемент находится в этом отношении сам с собой
-
Отнош называется антирефлексивным. если аГа никогда не выполняется.
-
Отнош называется симметричным, если аГЬ => ЬГа (для всех)
-
Отнош называется антисимметричным, если аГЬ и ЬГа одновременно невозможно.
-
Отнош называется асимметричным, если аГЬ, ЬГа => а=Ь
-
Отнош называется транзитивным, если аГЬ, ЬГс => аГс
-
Если отношение рефлексивно, симметрично и транзитивно, то оно наз. отношением эквивалентности.
Основное св-во: Если на мн-ве А задано отношение эквивалентности, то мн-во распадается на объединение непересекающихся классов эквивалентности, в каждом из которых все элементы эквивалентны друг другу.
10.
Отнош Г называется отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно.
Отнош Г называется отношением НЕстрогого порядка, если оно рефлексивно, асимметрично и транзитивно.
11.
Числовое сравнение двоичных наборов заключается в сравнении по первому биту
10002 > 01112
Очевидно, с таким отношением это мн-во линейно (вполне) упорядочено, т.е. любые наборы можем сравнить как числа.
Сравнение по Парето - сравнение по всем битам