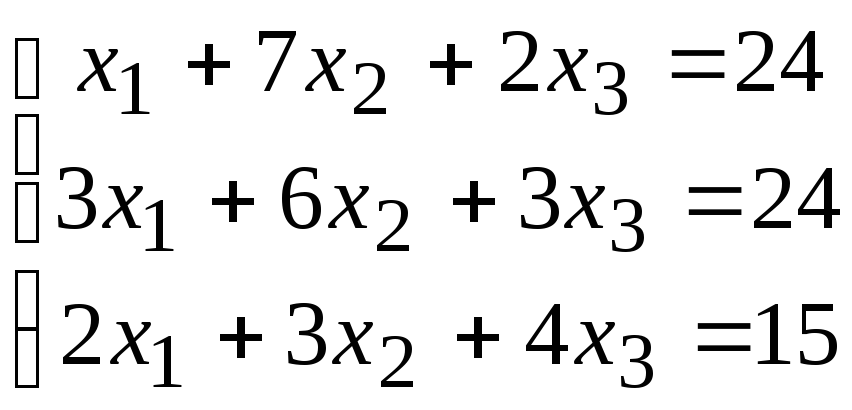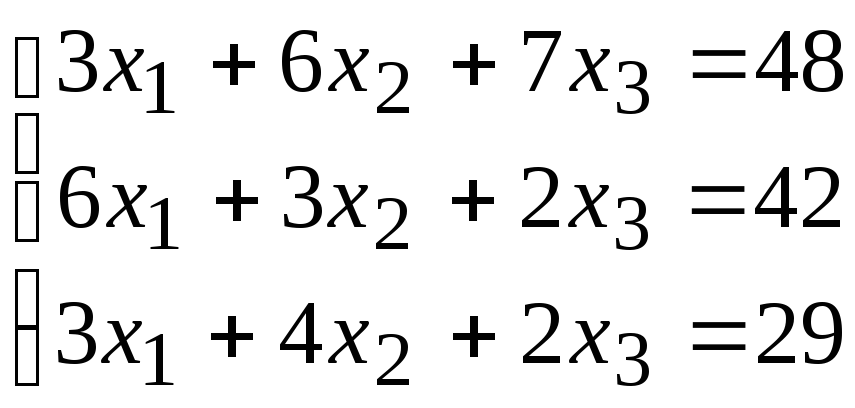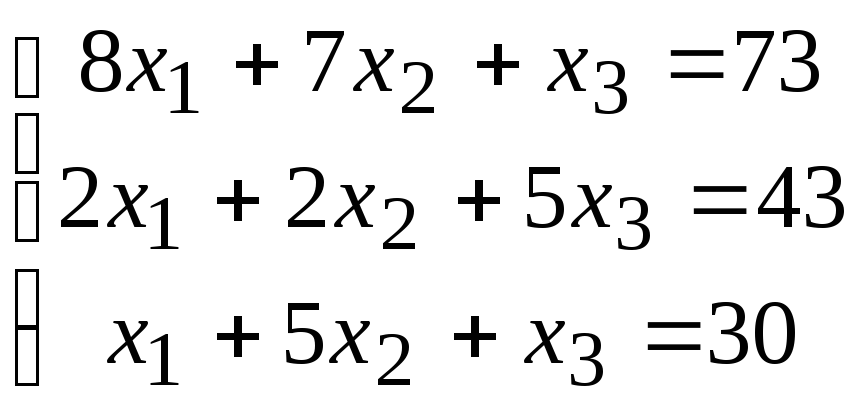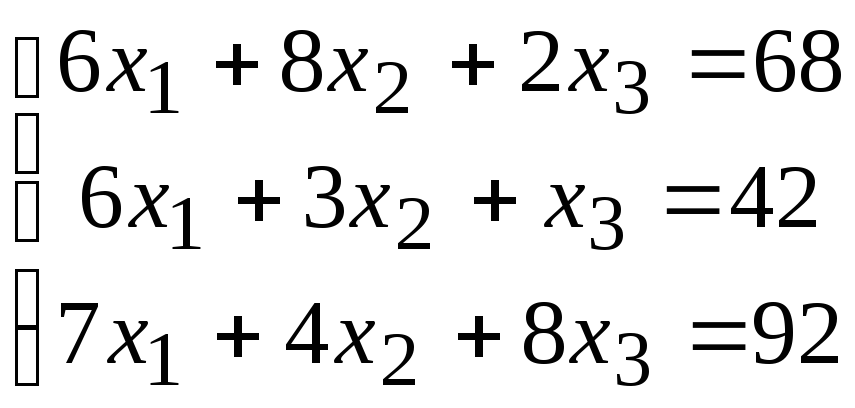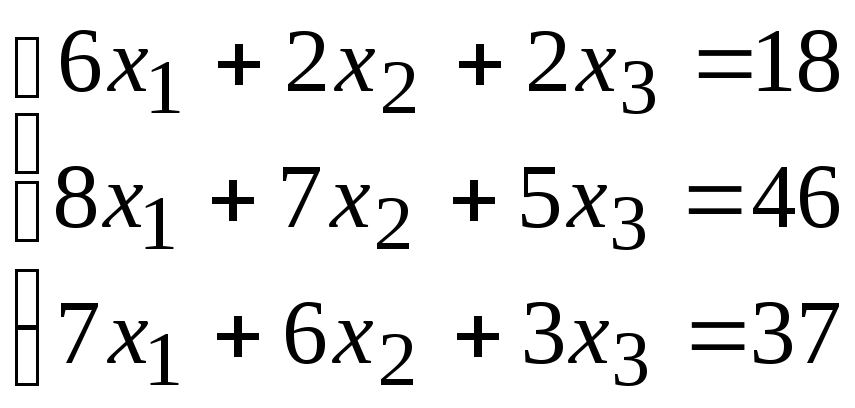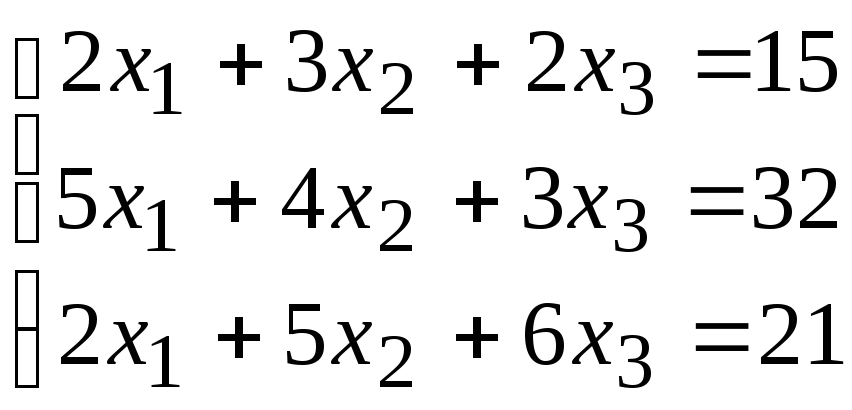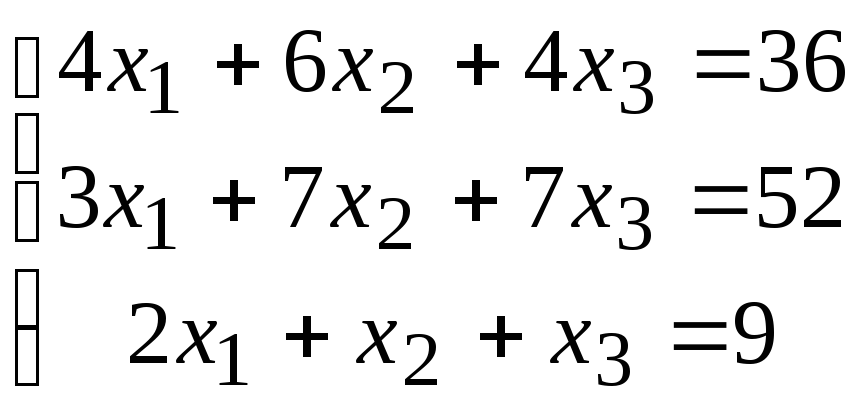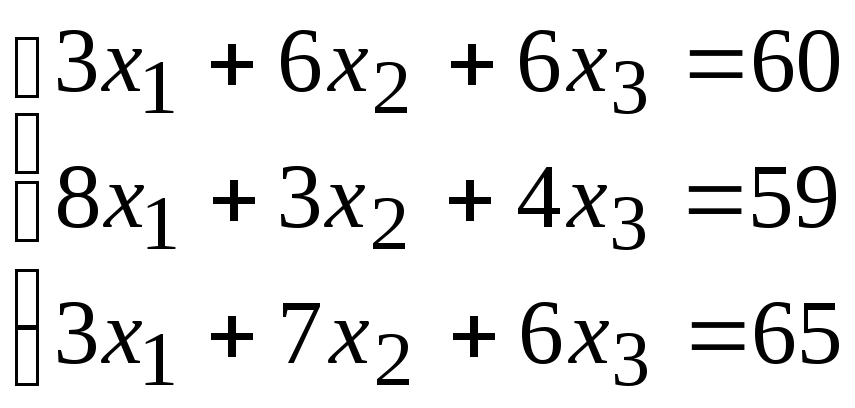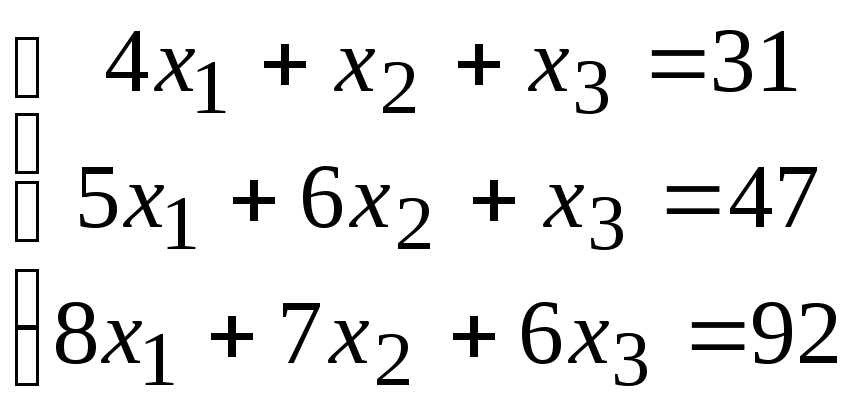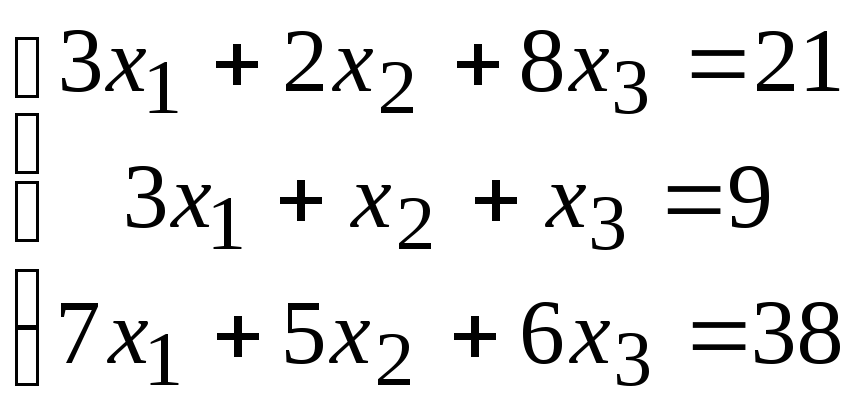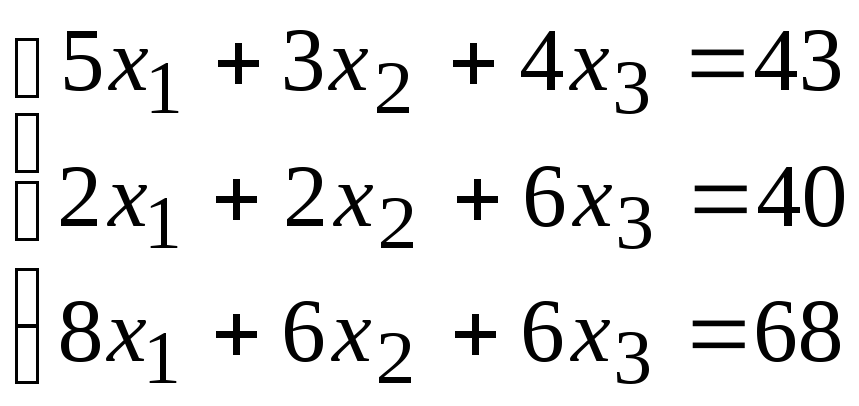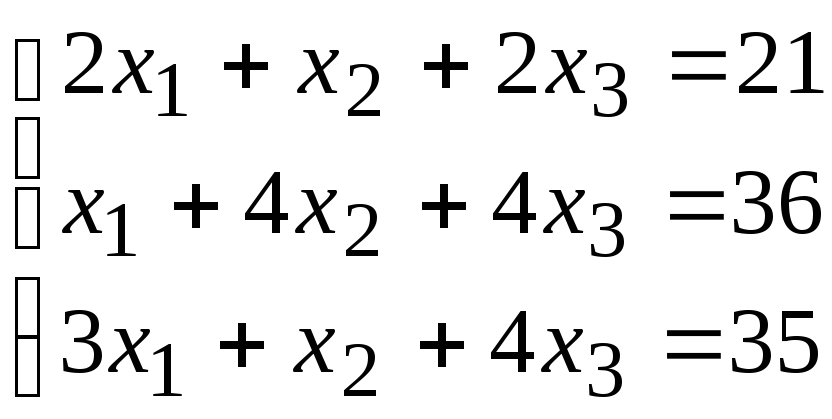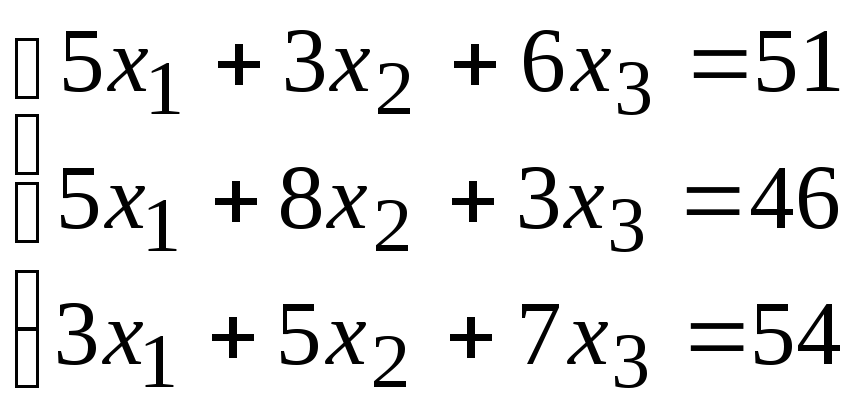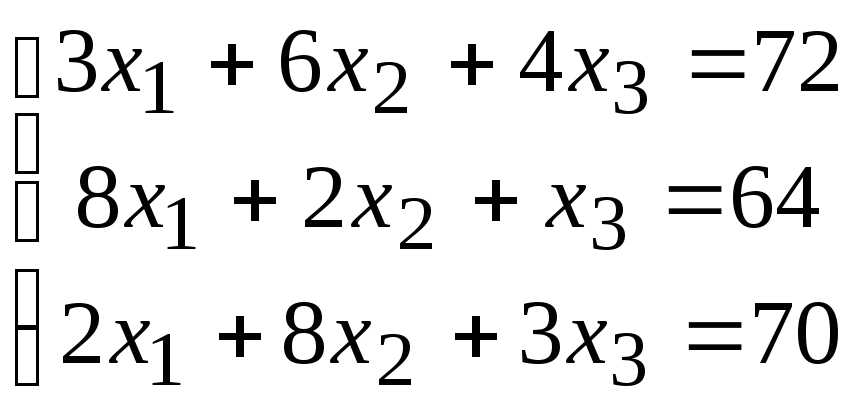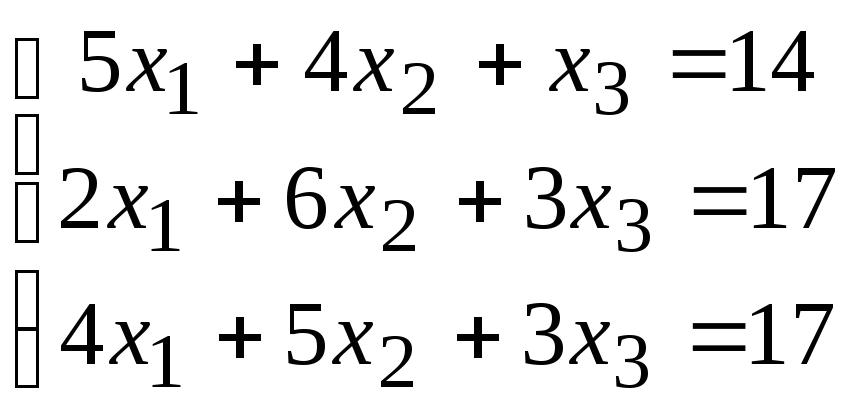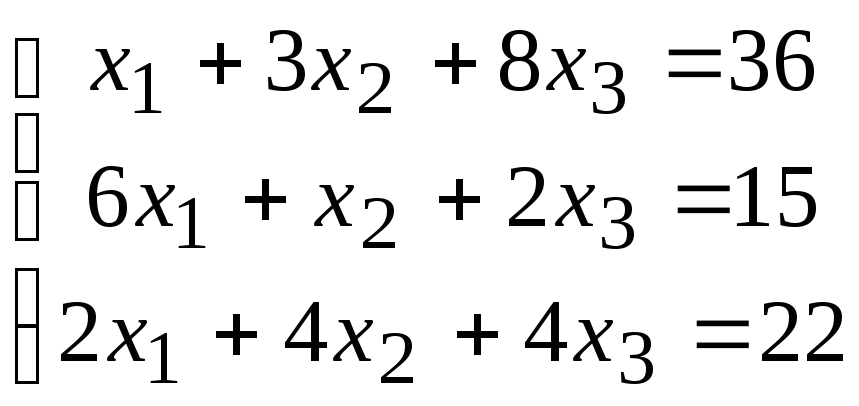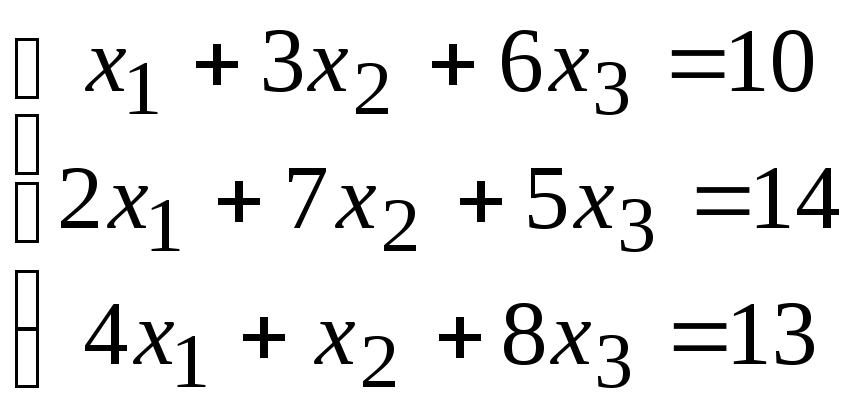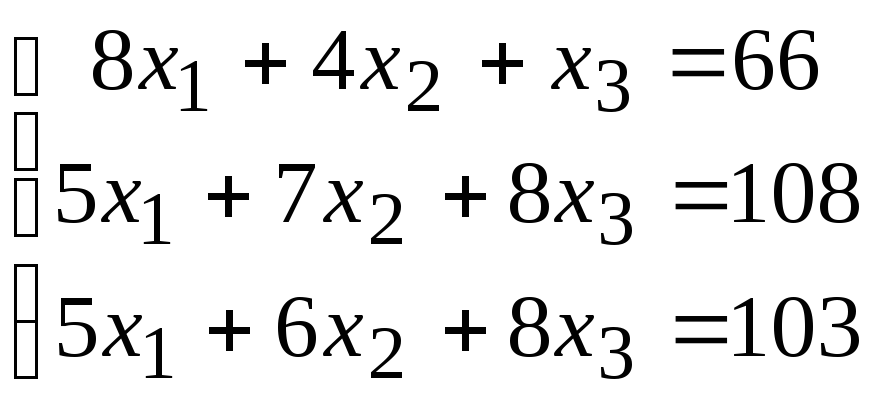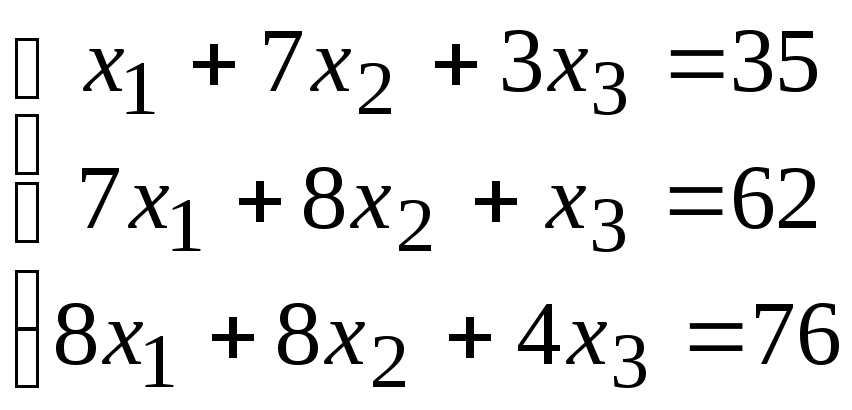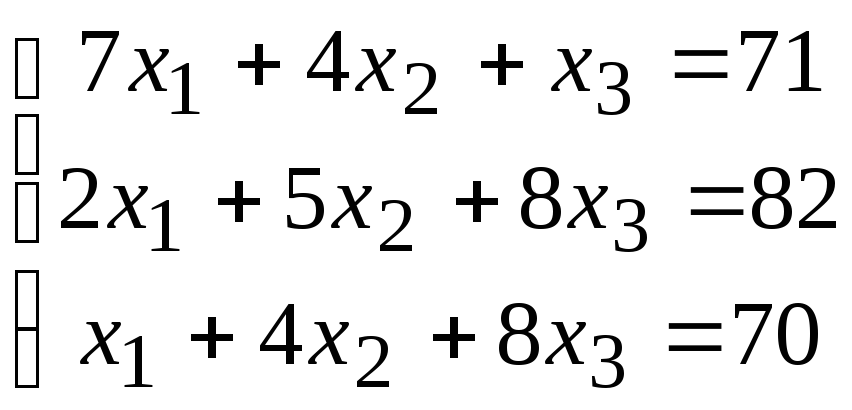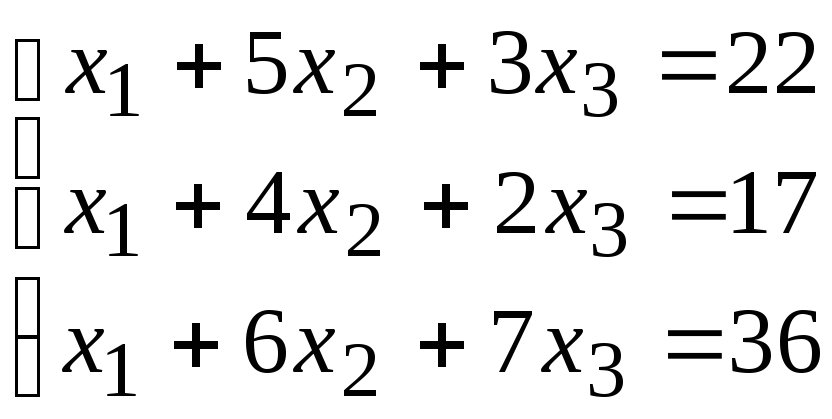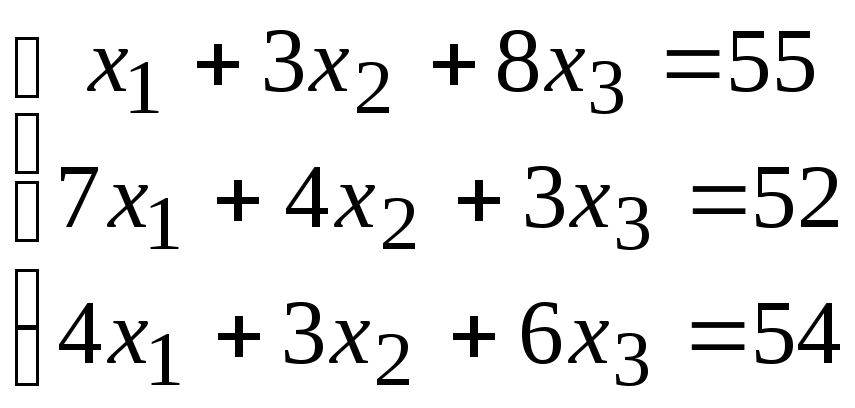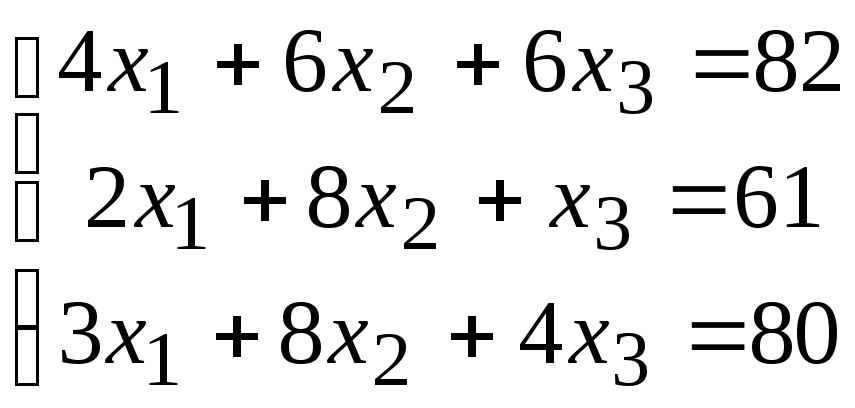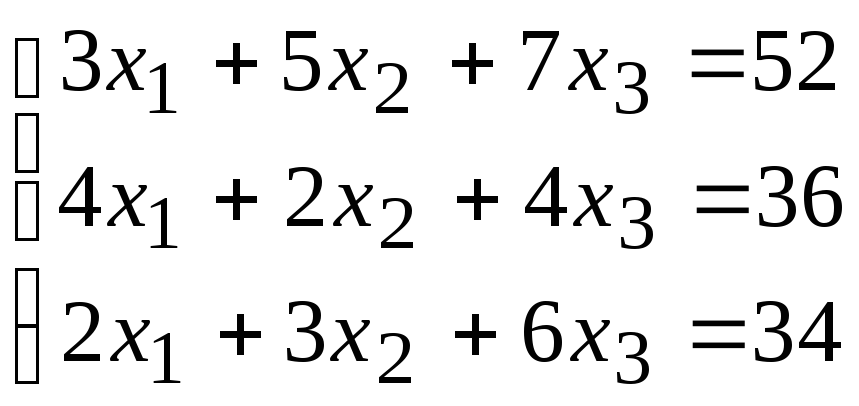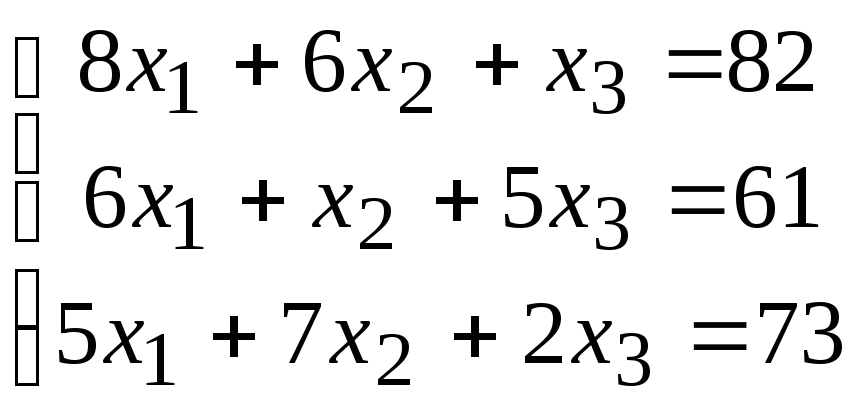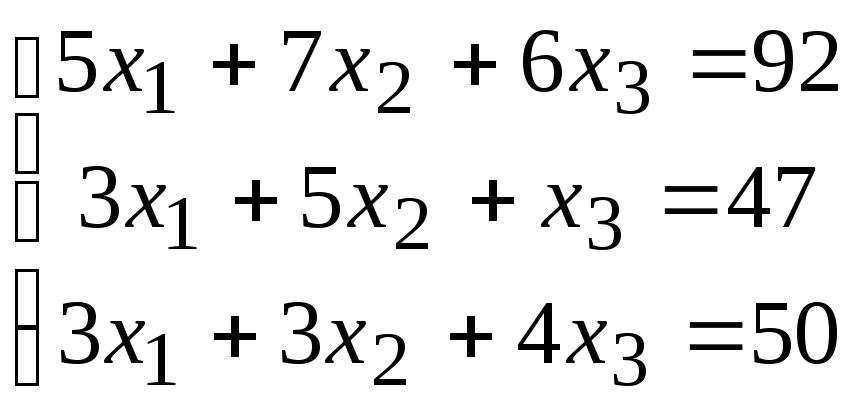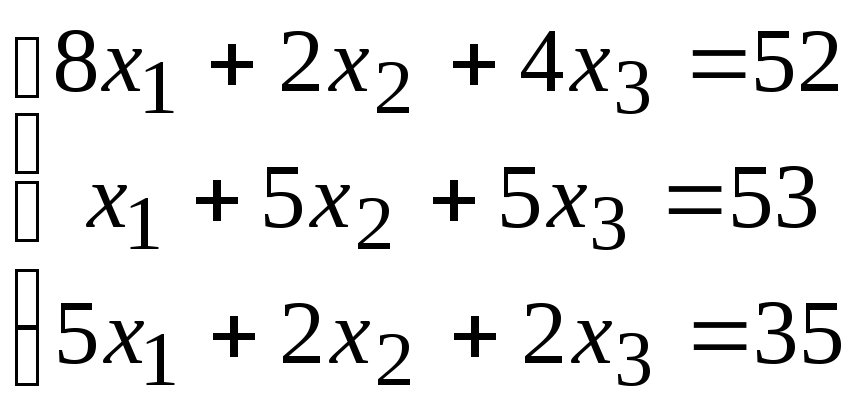2. Расчетно-графическая работа задание 1
Решить систему линейных алгебраических уравнений тремя способами: 1) методом Гаусса; 2) по формулам Крамера; 3) матричным способом.
|
1 |
|
2 |
|
3 |
|
|
4 |
|
5 |
|
6 |
|
|
7 |
|
8 |
|
9 |
|
|
10 |
|
11 |
|
12 |
|
|
13 |
|
14 |
|
15 |
|
|
16 |
|
17 |
|
18 |
|
|
19 |
|
20 |
|
21 |
|
|
22 |
|
23 |
|
24 |
|
|
25 |
|
26 |
|
27 |
|
|
28 |
|
29 |
|
30 |
|
Задание 2
Дано:
угол между векторами
и
равен
Значения
коэффициентов l,
m,
n,
k,
f
и модули векторов
и
приведены в табл.
Определите:
1)
длины
диагоналей параллелограмма, построенного
на векторах
и
;
2)
угол
между диагоналями;
3)
площадь
параллелограмма.
|
Вариант |
p |
q |
l |
m |
n |
k |
f |
|
1 |
2 |
5 |
4 |
1 |
2 |
7 |
6 |
|
2 |
6 |
4 |
1 |
5 |
1 |
2 |
3 |
|
3 |
3 |
7 |
1 |
4 |
7 |
2 |
4 |
|
4 |
3 |
3 |
4 |
3 |
6 |
7 |
6 |
|
5 |
3 |
7 |
3 |
4 |
6 |
6 |
3 |
|
6 |
1 |
4 |
6 |
4 |
7 |
4 |
4 |
|
7 |
1 |
1 |
3 |
4 |
4 |
1 |
6 |
|
8 |
2 |
1 |
4 |
3 |
1 |
2 |
3 |
|
9 |
1 |
7 |
6 |
7 |
4 |
7 |
4 |
|
10 |
7 |
4 |
7 |
1 |
6 |
4 |
6 |
|
11 |
1 |
2 |
4 |
6 |
6 |
7 |
3 |
|
12 |
2 |
7 |
3 |
6 |
2 |
3 |
4 |
|
13 |
2 |
4 |
4 |
1 |
3 |
7 |
6 |
|
14 |
1 |
6 |
2 |
1 |
5 |
6 |
3 |
|
15 |
5 |
4 |
3 |
6 |
3 |
5 |
4 |
|
16 |
1 |
1 |
3 |
2 |
7 |
4 |
6 |
|
17 |
1 |
3 |
7 |
4 |
6 |
1 |
3 |
|
18 |
1 |
7 |
4 |
7 |
7 |
1 |
4 |
|
19 |
1 |
3 |
3 |
7 |
1 |
2 |
6 |
|
20 |
5 |
7 |
5 |
5 |
7 |
7 |
3 |
|
21 |
5 |
1 |
7 |
5 |
7 |
3 |
4 |
|
22 |
2 |
4 |
6 |
4 |
6 |
4 |
6 |
|
23 |
5 |
7 |
3 |
7 |
1 |
4 |
3 |
|
24 |
4 |
7 |
1 |
4 |
6 |
4 |
4 |
|
Вариант |
p |
q |
l |
m |
n |
k |
f |
|
25 |
2 |
1 |
3 |
5 |
5 |
2 |
6 |
|
26 |
3 |
5 |
6 |
5 |
1 |
1 |
3 |
|
27 |
7 |
2 |
3 |
5 |
3 |
7 |
4 |
|
28 |
4 |
2 |
3 |
1 |
3 |
7 |
6 |
|
29 |
1 |
2 |
5 |
1 |
5 |
4 |
3 |
|
30 |
2 |
1 |
3 |
3 |
4 |
3 |
4 |
Задание 3
Даны
точки А и В. Из точки А выходит луч,
направленный по вектору
.
Найти координаты вектора
,
который пересекает луч, перпендикулярен
ему и равен
.
|
Вари-ант |
А |
В |
|
Вари-ант |
А |
В |
|
|
1 |
(-3;4;2) |
(1;12;3) |
|
16 |
(5;1;-3) |
(9;8;1) |
|
|
2 |
(1;2;-4) |
(4;6;8) |
|
17 |
(1;2;-1) |
(-9;-9;1) |
|
|
3 |
(-6;5;3) |
(-5;7;5) |
|
18 |
(5;-3;2) |
(8;3;0) |
|
|
4 |
(2;2;-1) |
(8;-4;6) |
|
19 |
(-4;9;-7) |
(4;-7;4) |
|
|
5 |
(4;-1;2) |
(10;5;9) |
|
20 |
(2;2;5) |
(1;4;3) |
|
|
6 |
(-1;-9;2) |
(0;9;8) |
|
21 |
(8;3;3) |
(4;-5;4) |
|
|
7 |
(-7;-6;3) |
(8;4;9) |
|
22 |
(-6;7;9) |
(6;-2;1) |
|
|
8 |
(-2;-1;5) |
(4;-3;8) |
|
23 |
(7;-5;-3) |
(-8;1;7) |
|
|
9 |
(3;-1;4) |
(5;1;5) |
|
24 |
(-8;2;5) |
(6;4;0) |
|
|
10 |
(1;-1;3) |
(5;0;11) |
|
25 |
(1;-7;-9) |
(2;5;3) |
|
|
11 |
(3;-1;0) |
(9;-3;9) |
|
26 |
(3;3;1) |
(9;-3;8) |
|
|
12 |
(-4;1;1) |
(3;5;5) |
|
27 |
(2;9;6) |
(8;-9;5) |
|
|
13 |
(-5;0;2) |
(1;-6;9) |
|
28 |
(5;-1;2) |
(6;-5;-6) |
|
|
14 |
(-7;5;5) |
(5;1;2) |
|
29 |
(-7;2;1) |
(-9;5;7) |
|
|
15 |
(1;8;3) |
(9;-8;-8) |
|
30 |
(3;2;5) |
(-1;6;-2) |
|
