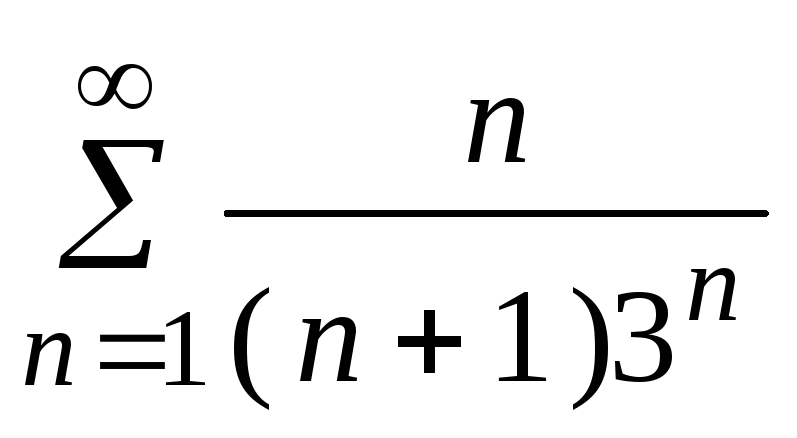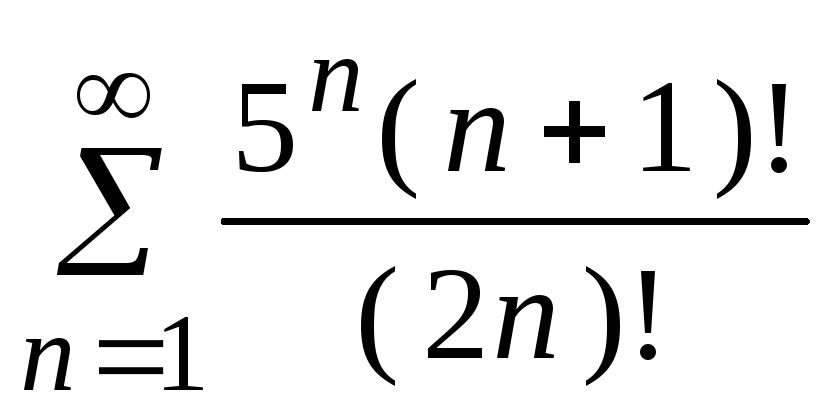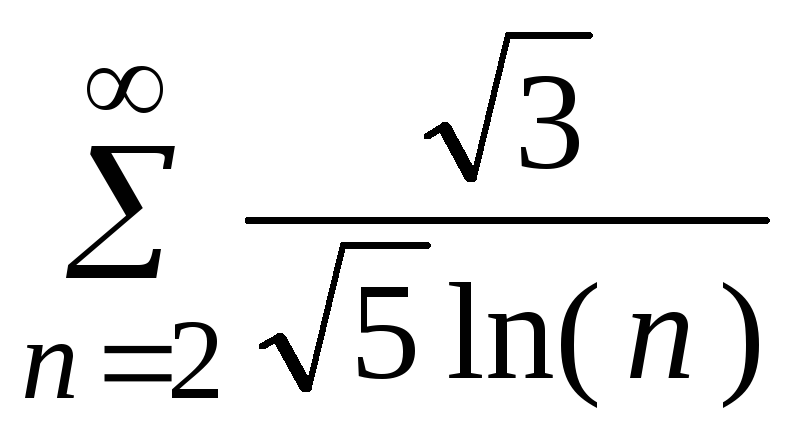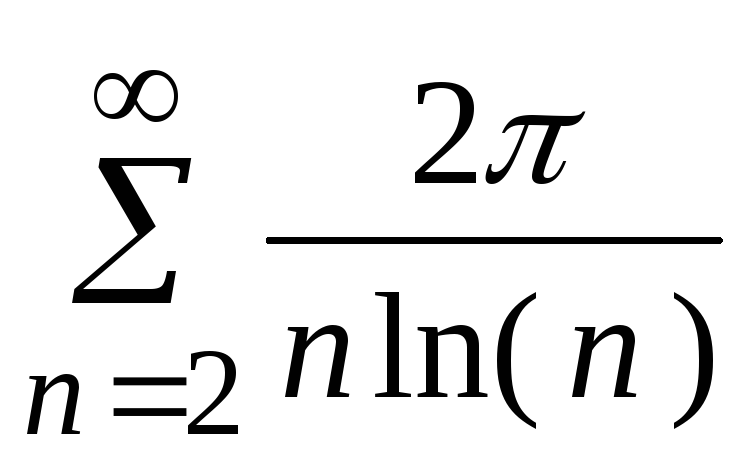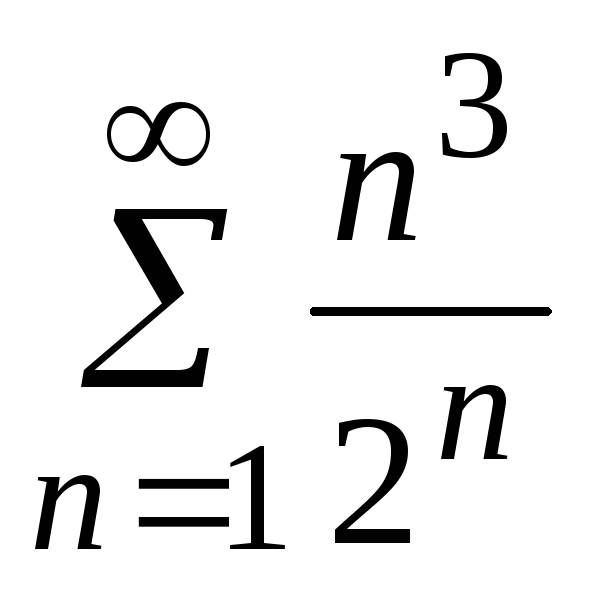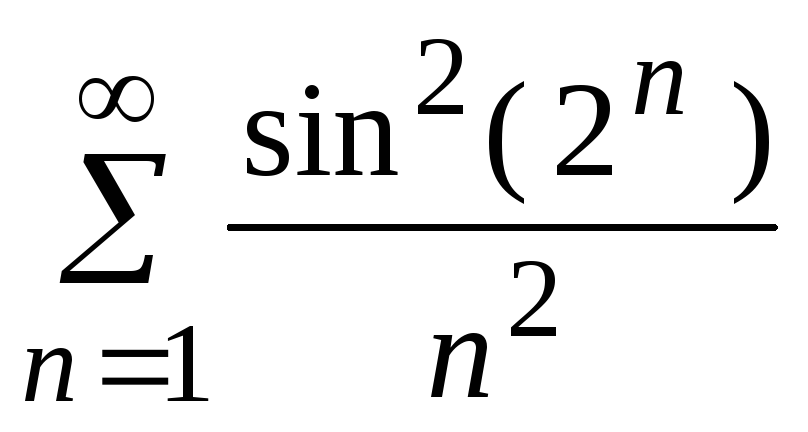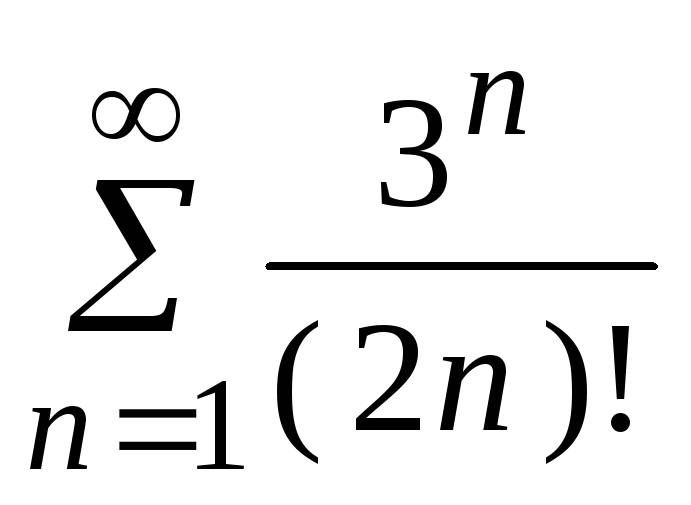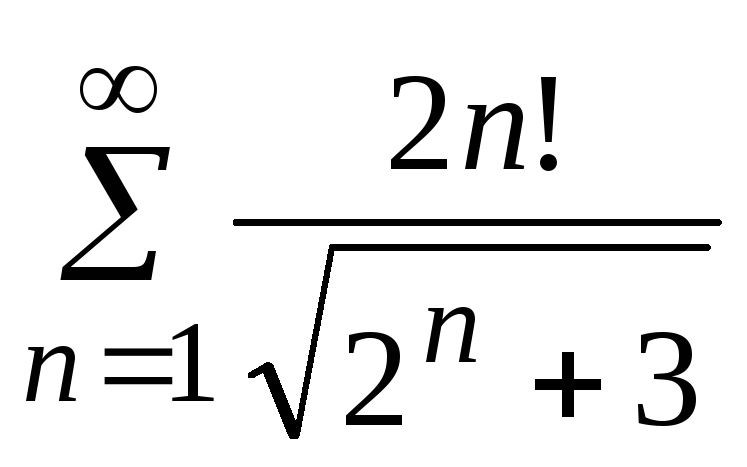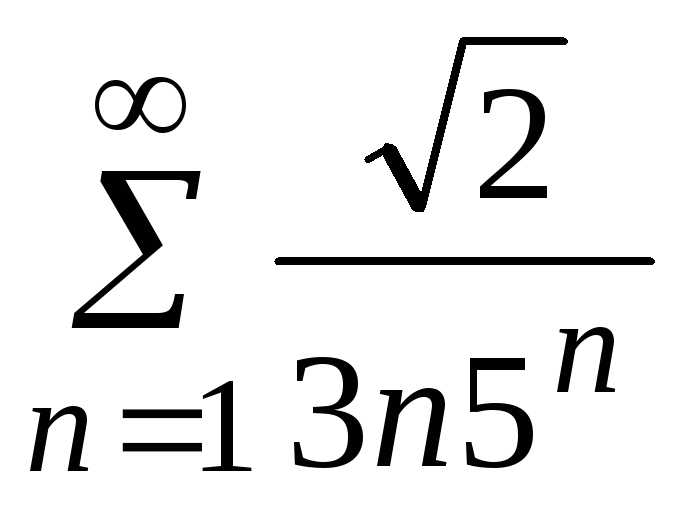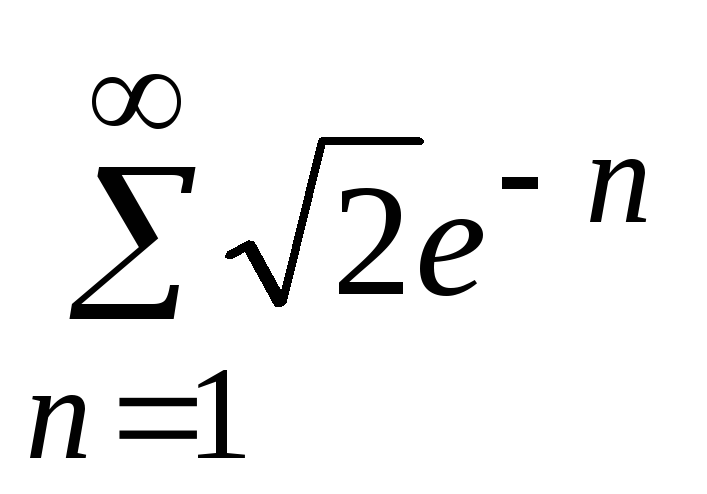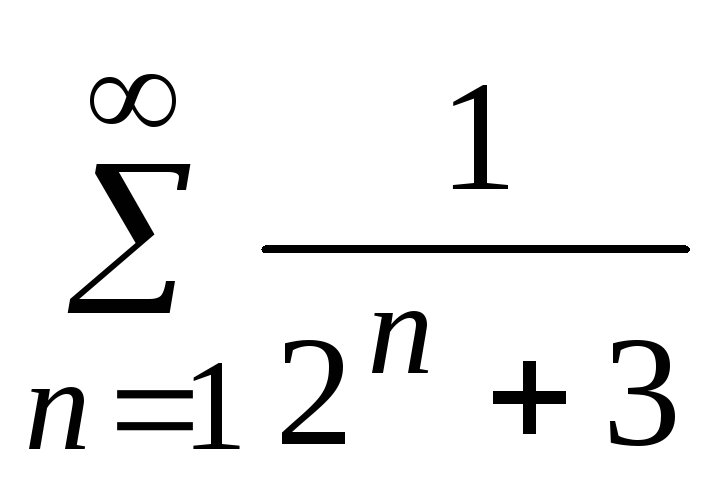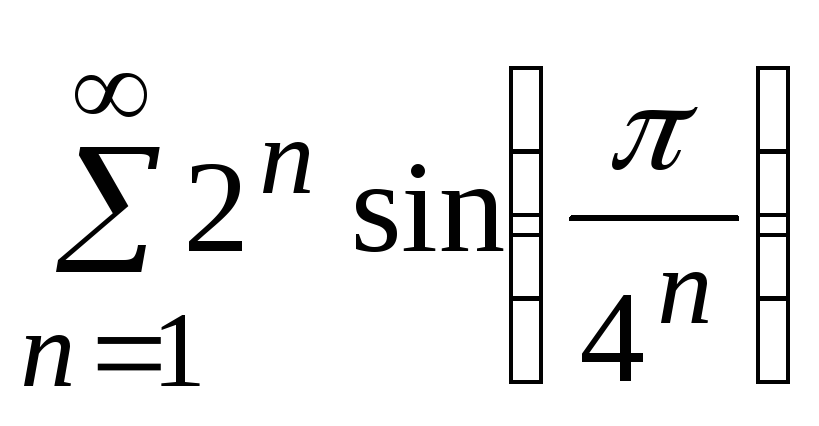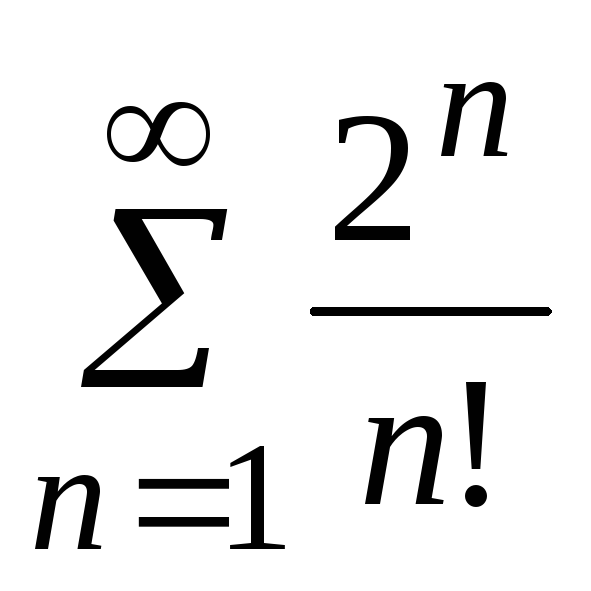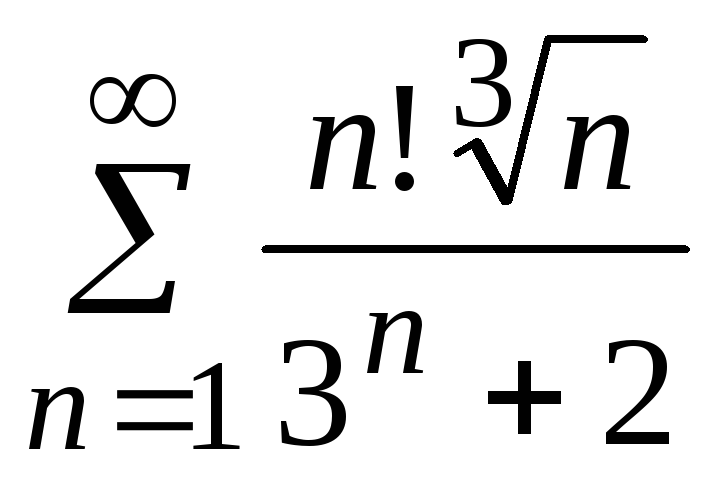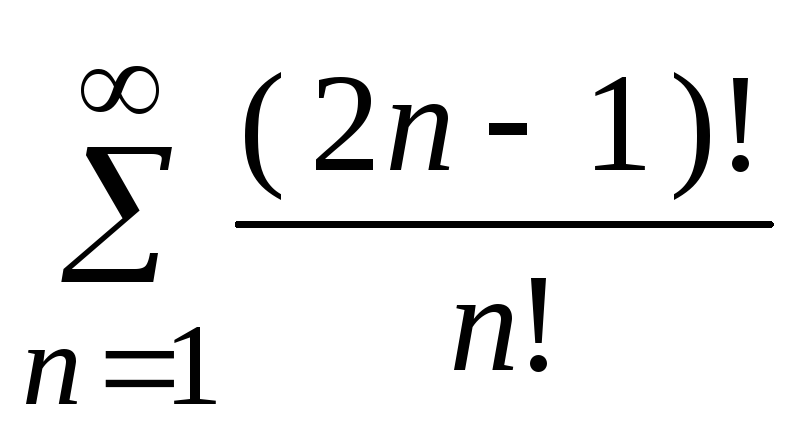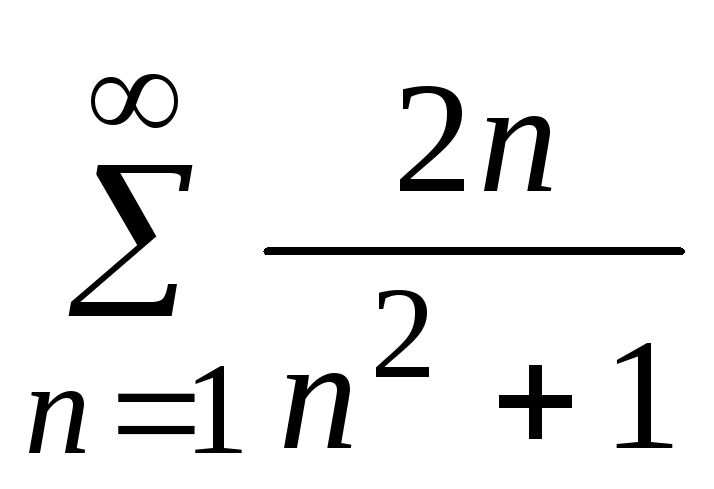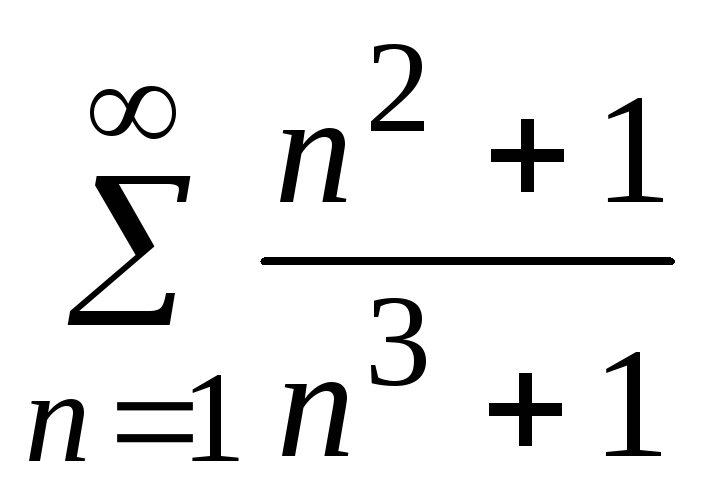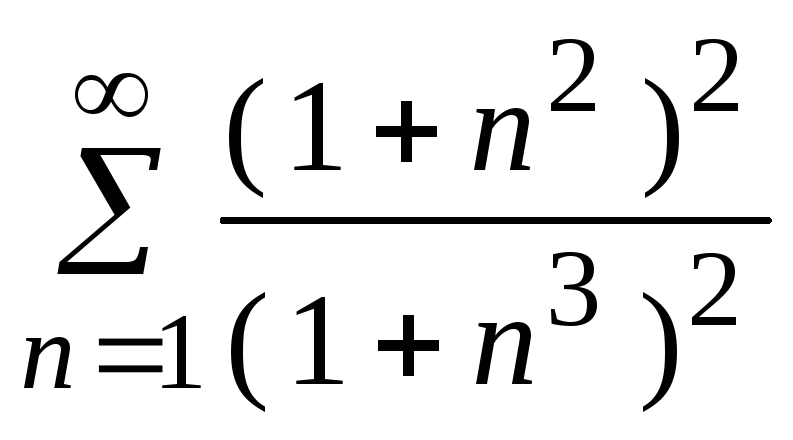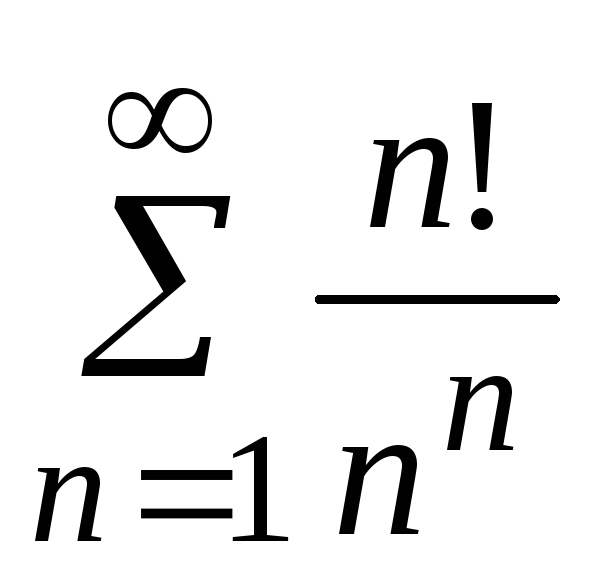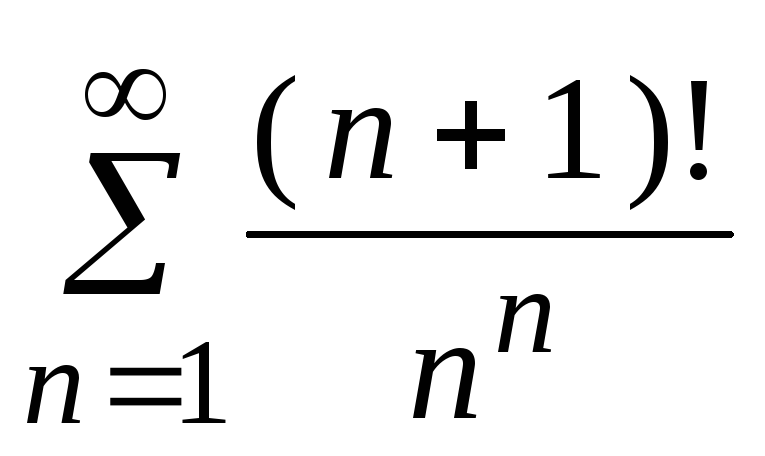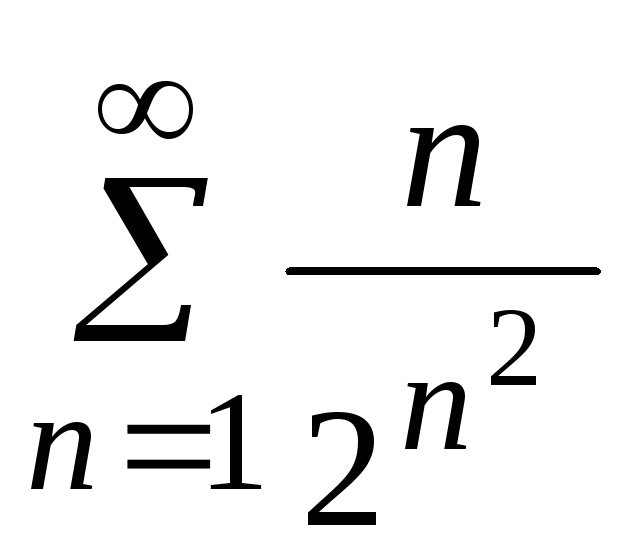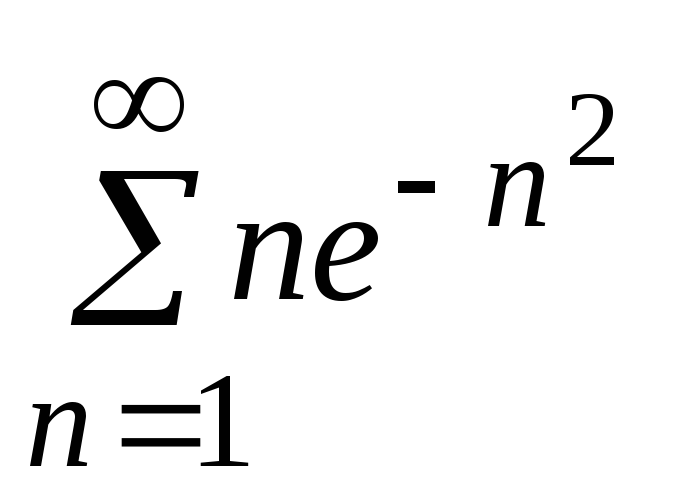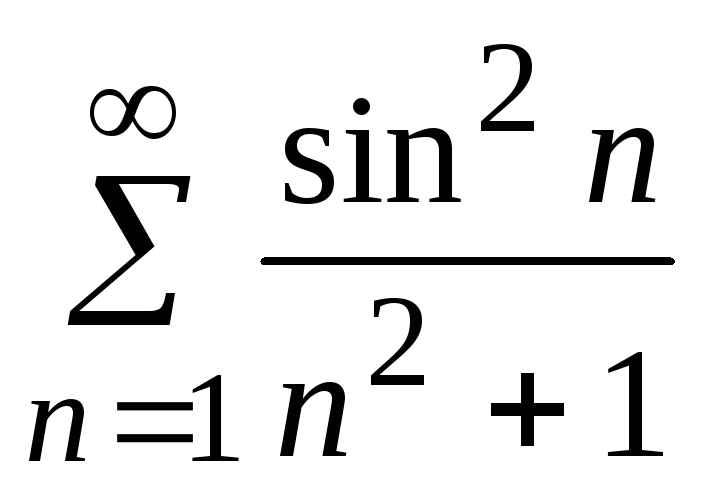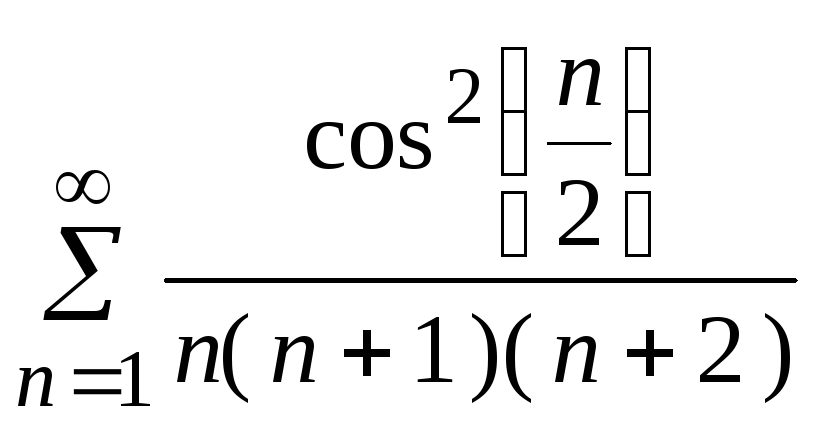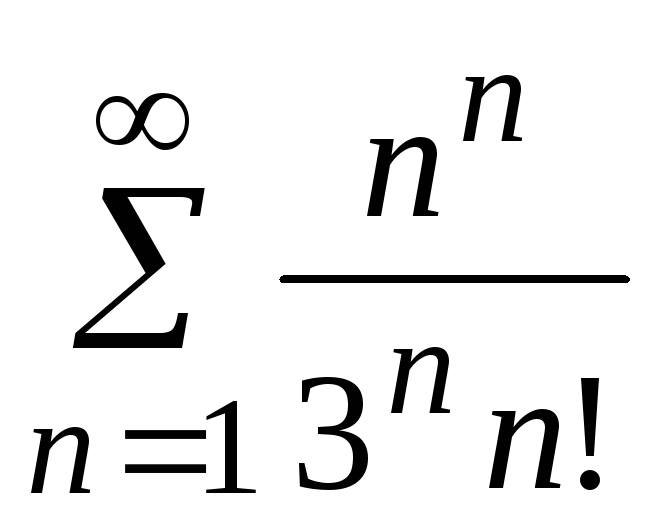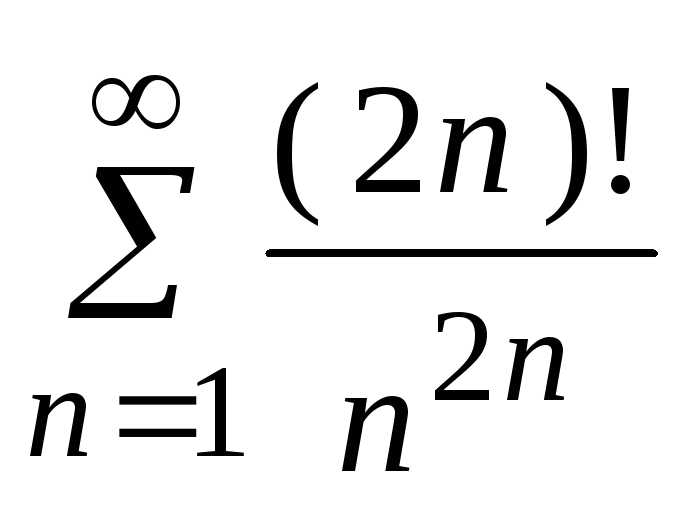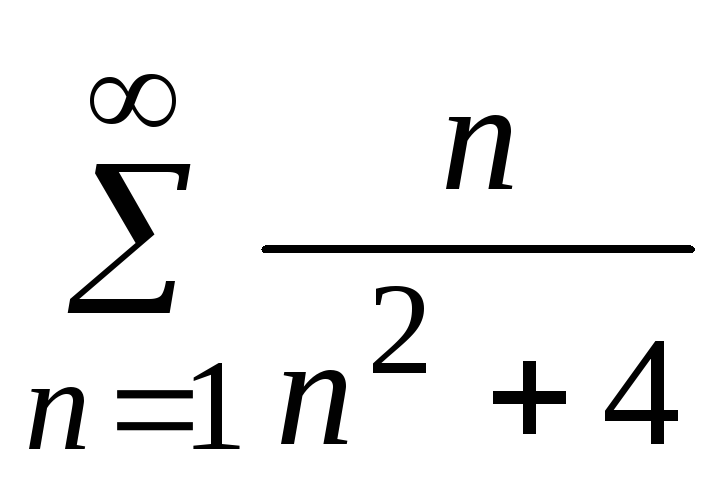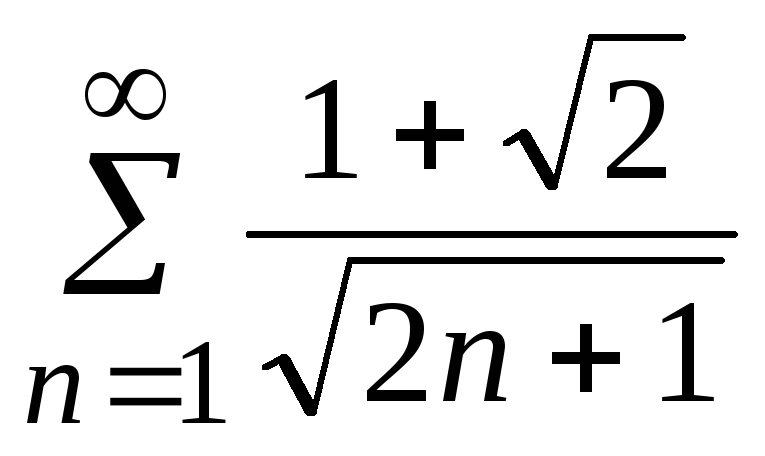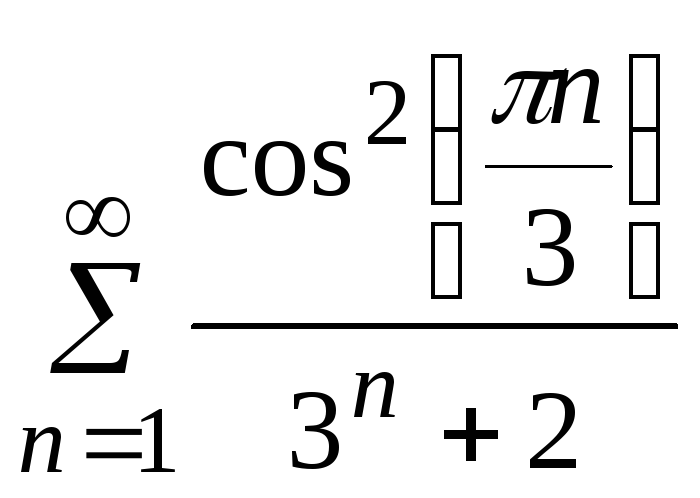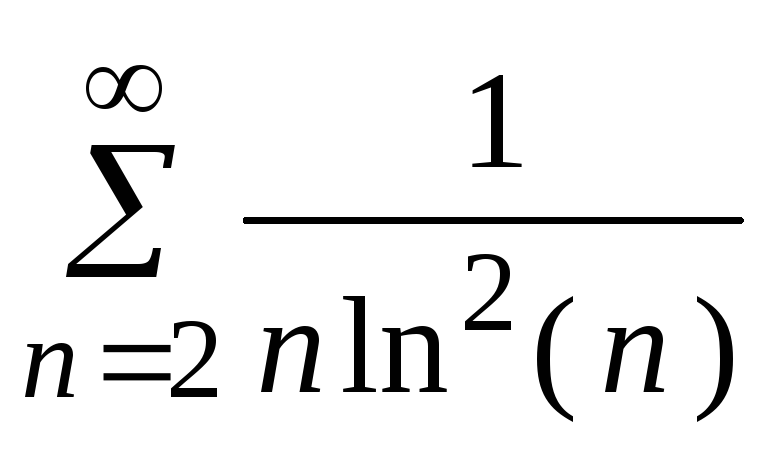5. Исследовать сходимость ряда:

Вариант	Ряд	Вариант	Ряд
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

6. Решить дифференциальное уравнение первого порядка:

Вариант	Уравнение	Вариант	Уравнение
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

Ответы

1.1. 1.2. 1.3. 1.4. 1.5. 1.6. 1.7. 1.8. 1.9. 1.10. 1.11. 0. 1.12. 1.13. 1. 14. -1.15. -2. 1.16. 2. 1.17. 4. 1.18. 2. 1.19. 2. 1.20. 2. 1.21. 1.22. 1.23. 3. 1.24. 1. 1.25. -1. 1.26. -49. 1.27. 2. 1.28. 0. 1.29. 2. 1.30. - 1.31. 0,1. 1.32. 1. 1.33. 1. 1.34. 0,5. 1.35. 2. 1.36. .1.37.1. 1.38. 1.39. 1.40. . 1.41. .1.42. .1.43. .1.44. .1.45. 9. 1.46. 1.47. 1. 1.48. 1.49. 1.50. 1.51. 0. 1.52. 1.53. 1.54. 1.55. 0. 1.56. 1.57. 1.58. 1.59. 1.60. 1.61. 0. 1.62. 1. 1.63. 1.64. x. 1.65. 1.66. 1.67. 1.68. 1.69. 3. 1.70. 1.71. 0. 1.72. 1.73. 1.74. 0. 1.75. 1.76. 2. 1.77. 1.78. 1. 1.79. 1. 1.80. 1.81. -3. 1.82. 1.83. 1.84. 1.85. -1. 1.86. 1. 1.87. 1.88. 0. 1. 89. -1.90. 0.

2.1..2.2.. 2.3..2.4. 2.5.2.6.. 2.7..2.8.. 2.9..2.10.. 2.11..2.12.. 2.13..2.14.. 2.15..2.16.. 2.17..2.18.. 2.19.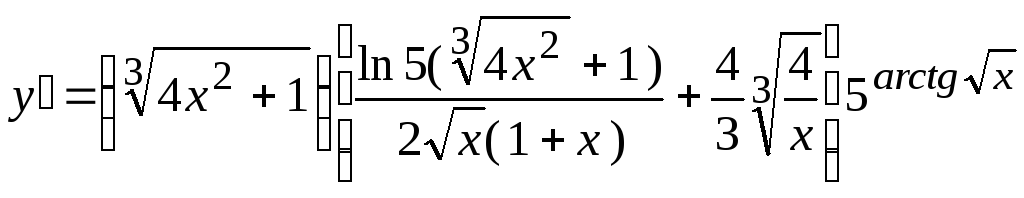. 2.20..2.21.. 2.22.. 2.23.2.24. 2.25. 2.26.2.27. 2.28..2.29.2.30.. 2.31..2.32.2.33. 2.34.2.35. 2.36.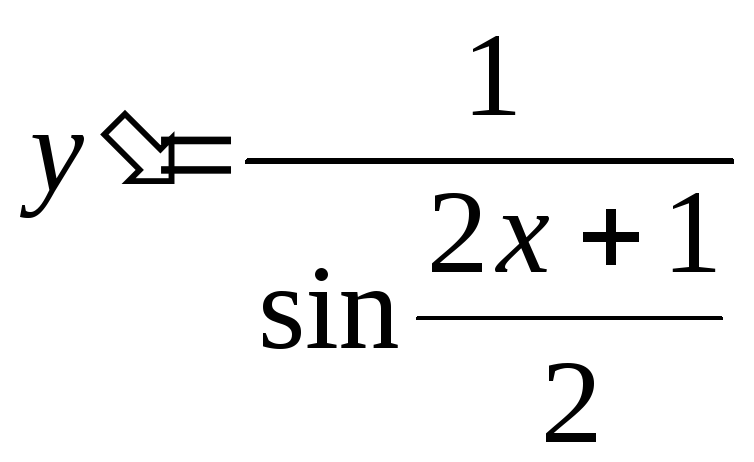.2.37.. 2.38.2.39.2.40. 2.41. 2.42. 2.43.. 2.44.. 2.45.2.46. 2.47. 2.48. 2.49.

2.50..

2.51.2.52.

2.53..

2.54.2.55.

2.56.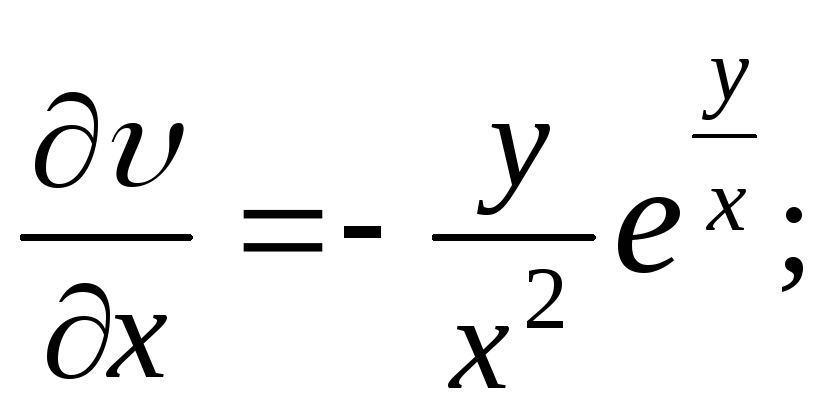2.57.

2.58.2.59.2.60.

2.61.

2.62.

2.63.2.64.

2.65.2.66.

2.67.2.68.2.69.2.70.2.71.2.72.2.73.

2.74.

2.75.2.76.2.77.2.78.2.79.2.86.2.87.2.88.2.89.2.90.2.91.2.92.2.93.

3.1. Максимум в точке

3.2. Минимум в точке; максимум в точке

3.3. Максимум в точке минимум в точке

3.4. Максимум в точке минимум в точке

3.5. Функция монотонно возрастает в интервале .

3.6. Точки экстремума При четном точкиявляются точками минимума, где; при нечетномточкиявляются точками максимума, где

3.7.

3.8.

3.9. Экстремумов нет.

3.10.

3.11.

3.12.

3.13. Максимум в точке ; функция имеет перегиб в точкахи.

3.14. Минимум в точке максимум в точке. В точкефункция имеет перегиб.

3.15. В точке функция имеет минимум. В точкефункция имеет разрывII рода.

3.16. Функция определена и непрерывна на всей числовой оси. График пересекает оси координат в точках и. Асимптот нет.Точка перегиба.

3.17. Функция определена и непрерывна на всей числовой оси. График пересекает оси координат в точках и. Асимптот нет. Точки перегиба и.

3.18. – точки разрываII рода. График пересекается с осями в начале координат. Асимптоты и

Точка перегиба .

3.19. – точка разрываII рода. График пересекает оси координат в точках и. АсимптотыиТочек перегиба нет (гипербола).

3.20. Функция определена и непрерывна всюду. График пересекается с осями в начале координат. Асимптота Экстремумов нет, функция всюду возрастает. Точки перегиба,,.

3.21. Функция определена и непрерывна всюду. График пересекает оси координат в точках и. АсимптотаЭкстремумов нет, функция всюду убывает. Точки перегибаи.

3.22. Область определения . График пересекает оси координат в точкахи– концевая точка. Асимптот нет.Точек перегиба нет.

3.23. Минимум при .

3.24. Максимум при ; минимум при.

3.25. Максимум при ; минимум при

3.26. Функция имеет минимум в точке . В точке– имеет место разрывII рода.

3.27. Максимум минимумв точке– перегиб; в точкахифункция имеет разрывыII рода.

3.28. В точке – минимум. В точкефункция имеет разрывII рода.

3.29. – максимум; в точкефункция имеет разрывII рода; в точке функция имеет перегиб.

3.30. Минимум ; максимум;– точка перегиба.

3.31. В точках разрывыII рода; максимум в точке ;и– вертикальные асимптоты;– горизонтальная асимптота.

3.32. – точка разрываII рода; – горизонтальная асимптота;– максимум;– точка перегиба.

3.33. и– точки разрываII рода; вертикальные асимптоты: ,; горизонтальная асимптота;– максимум.

3.34. – точка разрываII рода; – горизонтальная асимптота;– вертикальная асимптота;– точка минимума.

3.35. – точка разрываII рода; – вертикальная асимптота;– точка минимума;– точка перегиба.

3.36. – вертикальная асимптота; – горизонтальная асимптота;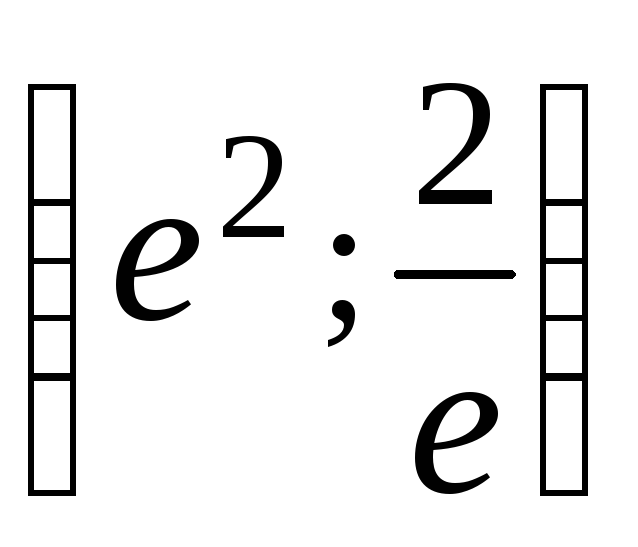– максимум;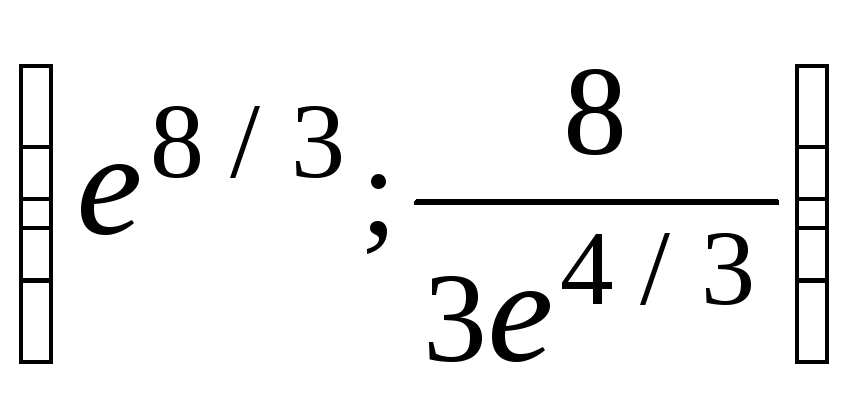– точка перегиба.

3.37. х=0 – вертикальная асимптота; y=x- наклонная асимптота; () – минимум.

3.38. – горизонтальная асимптота; ,– вертикальные асимптоты;- функция выпукла вверх;– функция выпукла вниз.

3.39. – наклонная асимптота;– функция выпукла вниз;– функция выпукла вверх;и– точки перегиба.

3.40. – точка максимума;– точка минимума;– точка перегиба.

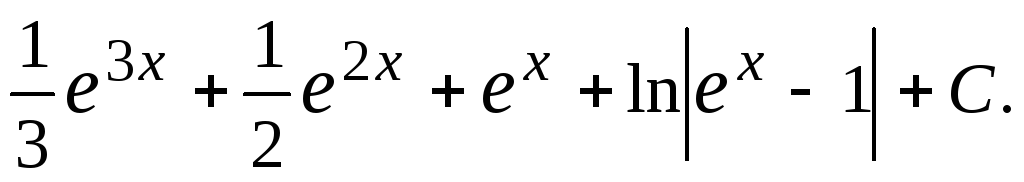4.1. 4.2. 4.3. .4.4. .4.5. 4.6. 4.7. 4.8. 4.9. 4.10. 4.11. 4.12. 4.13. 4.14. 4.15. 4.16.4.17. 4.18. 4.19. 4.20. 4.21.