
- •Введение
- •I. Вычисление пределов функции
- •Найти следующие пределы:
- •2.1. 2.2.
- •2.54. 2.55.
- •III. Исследование функций и построение графиков
- •Исследовать функции и построить их графики:
- •Формула замены переменной в определенном интеграле
- •Вычисление площади поверхности вращения
- •Вычисление объема тела вращения
- •Понятие несобственного интеграла
- •6.34. 6.35.
- •7.1. 7.2.
- •Линейные дифференциальные уравнения первого порядка
- •Уравнение Бернулли.
- •Уравнения высших порядков, допускающие понижение порядка
- •4. Вычислить площадь фигуры, ограниченной линиями:
- •5. Исследовать сходимость ряда:
- •6. Решить дифференциальное уравнение первого порядка:
- •2.51.2.52.
- •4.22. 4.23.4.24.
- •8.1. 8.2. 8.3. 8.4. 8.5. 8.6. 8.7. 8.8. 8.9. 8.10. 8.11.
7.1. 7.2.
7.3.
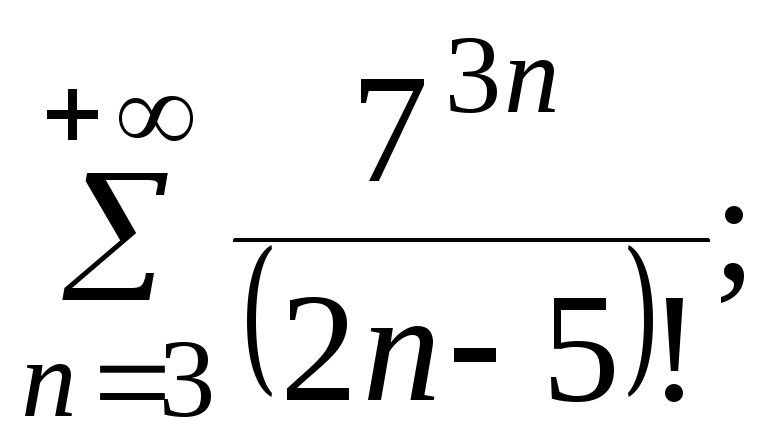 7.4.
7.4.
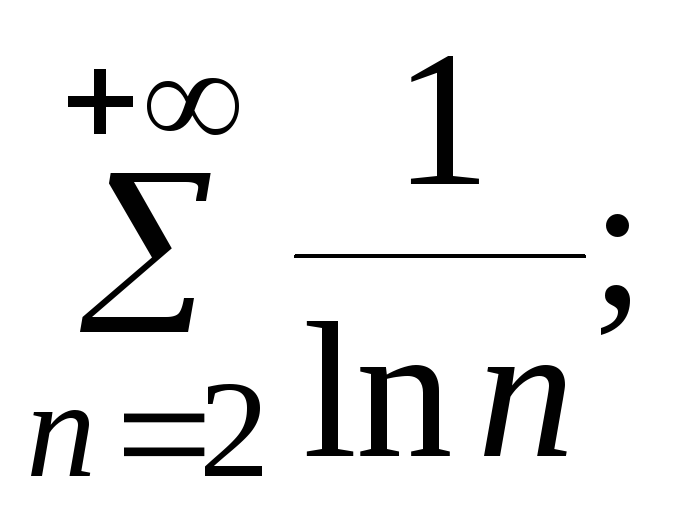
7.5.
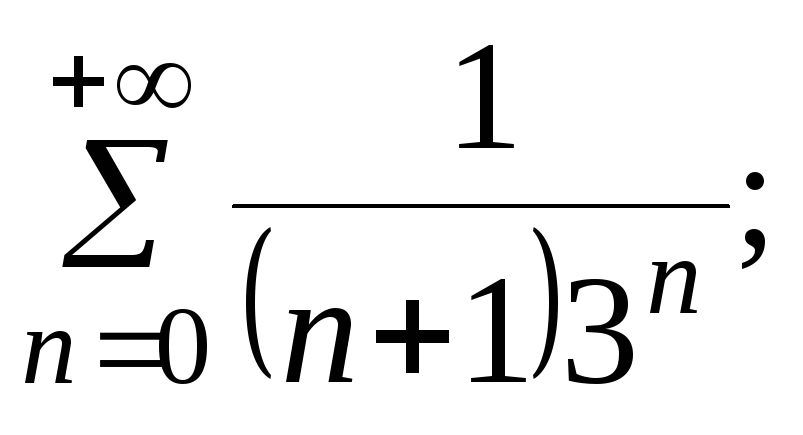 7.6.
7.6.
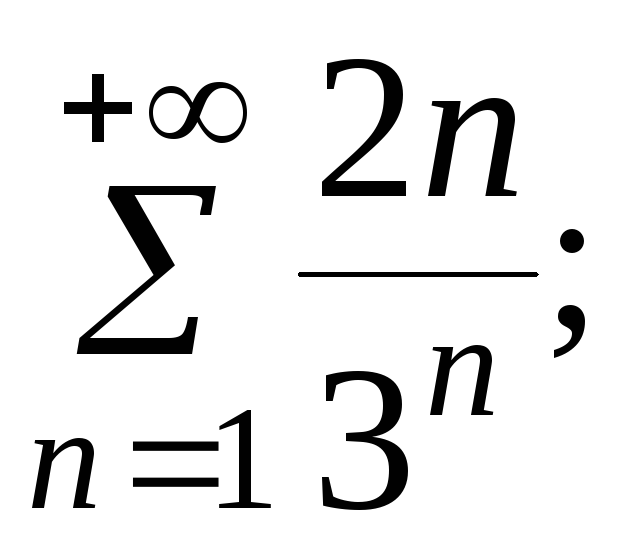
7.7.
 7.8.
7.8.
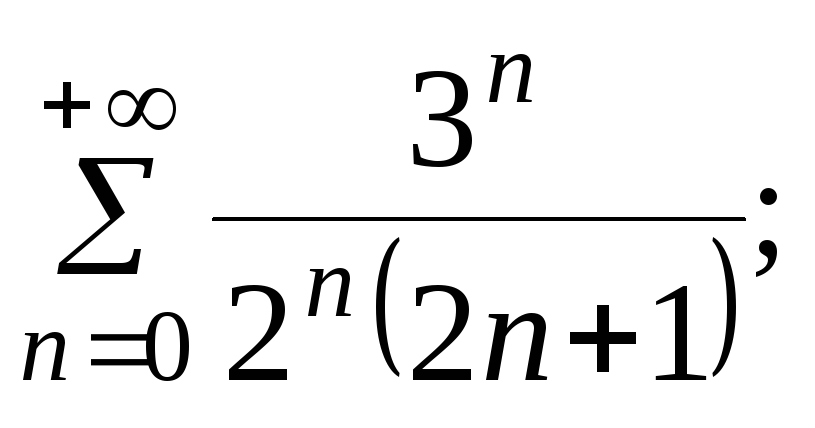
7.9.
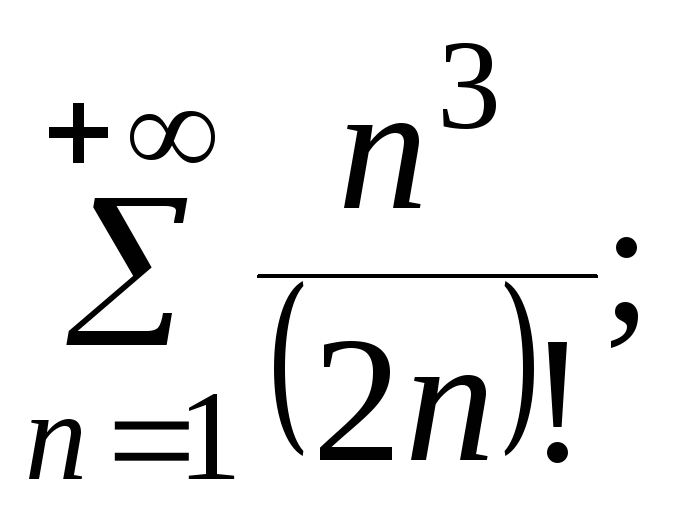 7.10.
7.10.
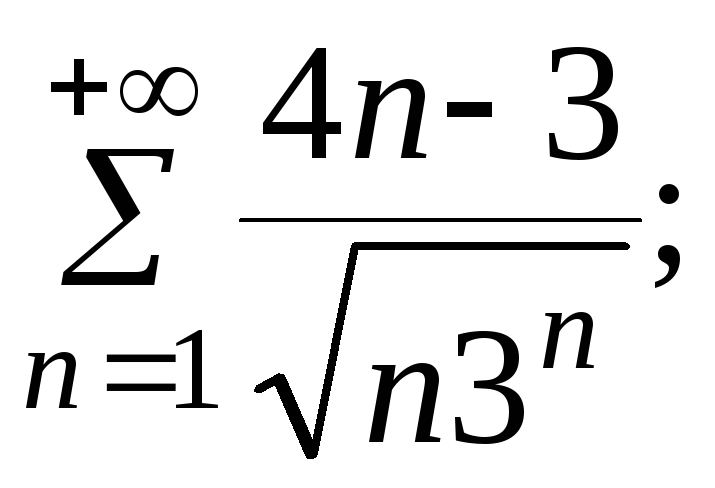
7.11.
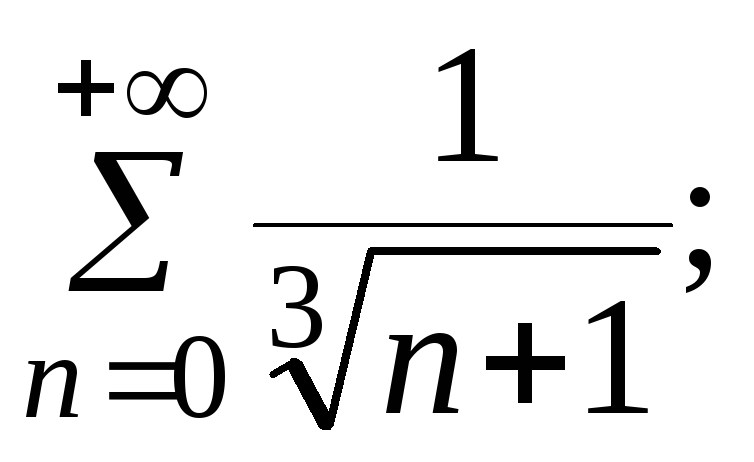 7.12.
7.12.
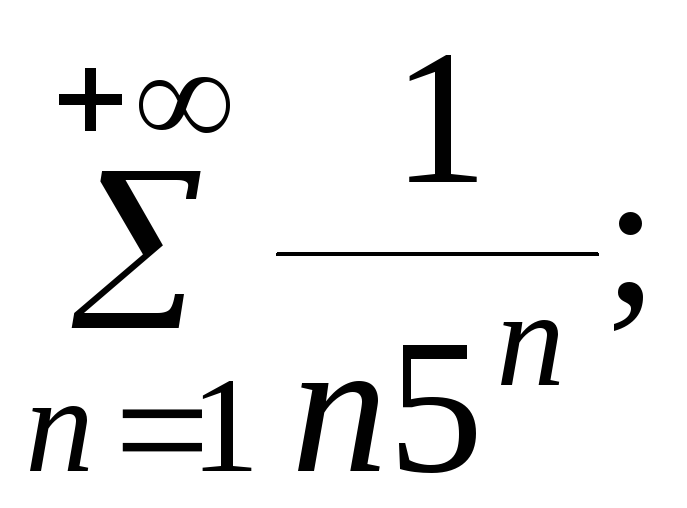
7.13.
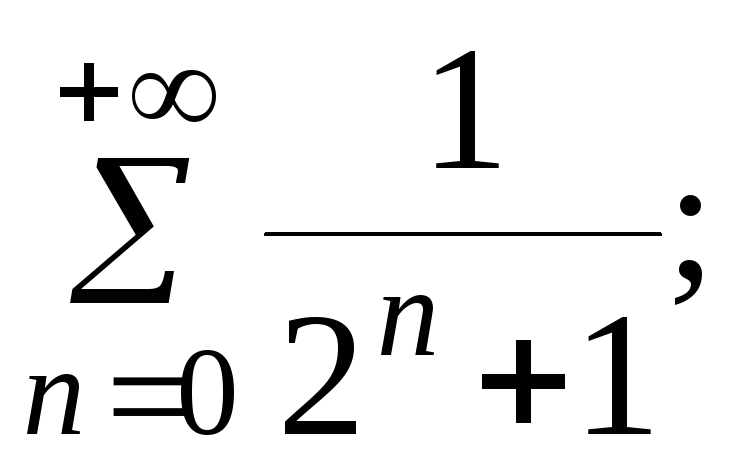 7.14.
7.14.
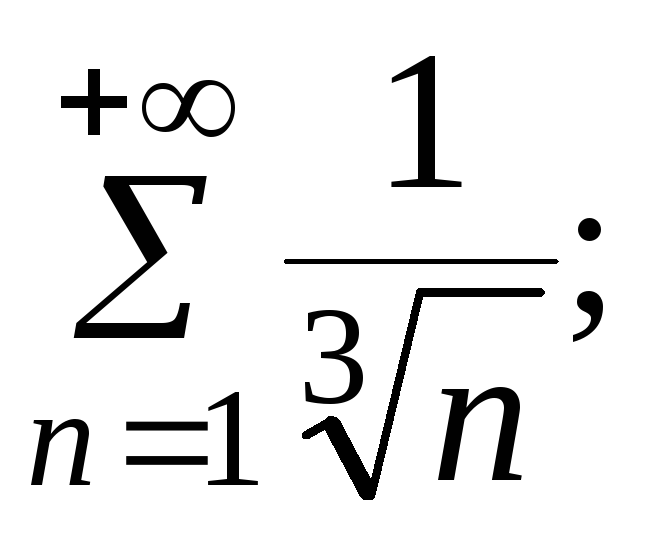
7.15.
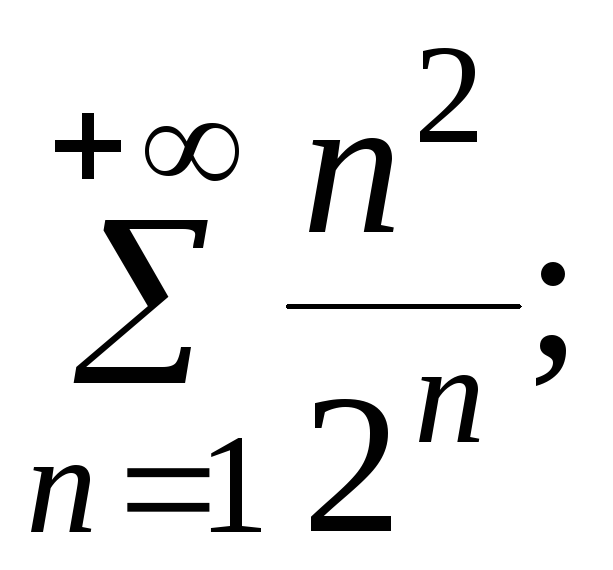 7.16.
7.16.
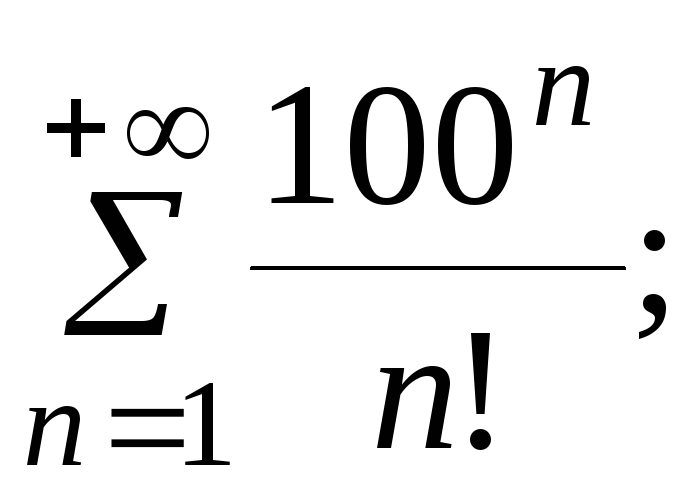
7.17.
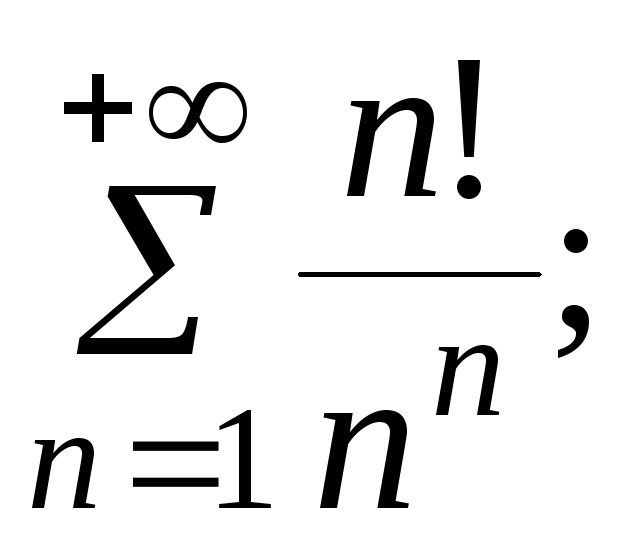 7.18.
7.18.
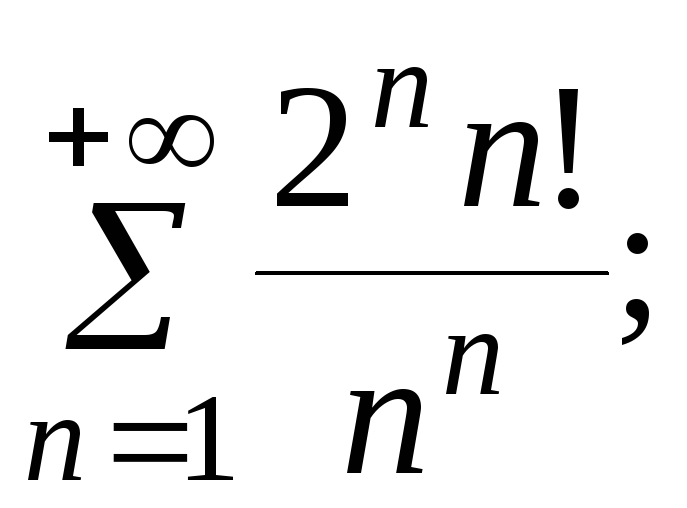
7.19.
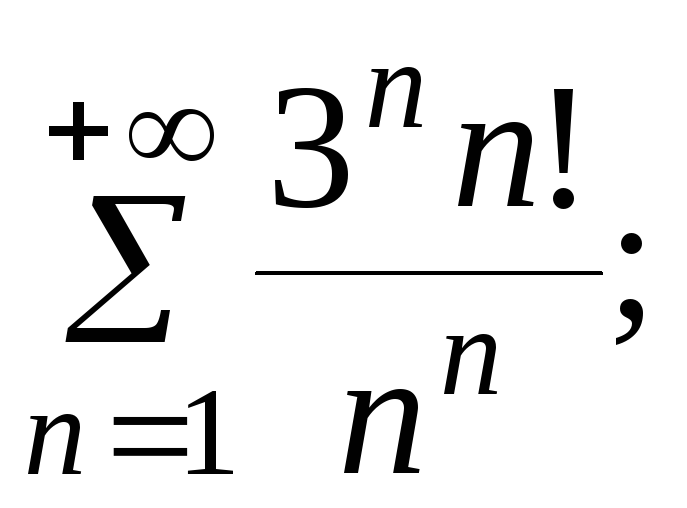 7.20.
7.20.
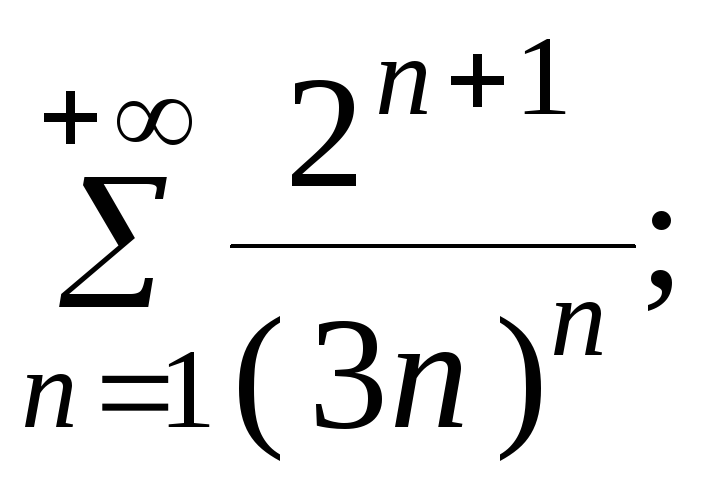
7.21.
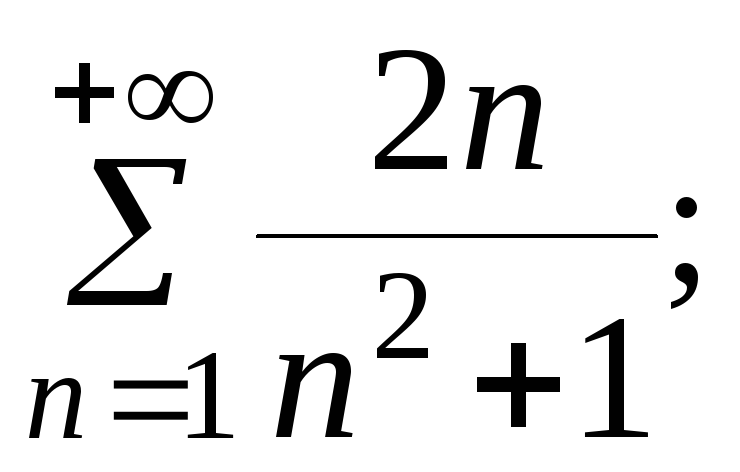 7.22.
7.22.
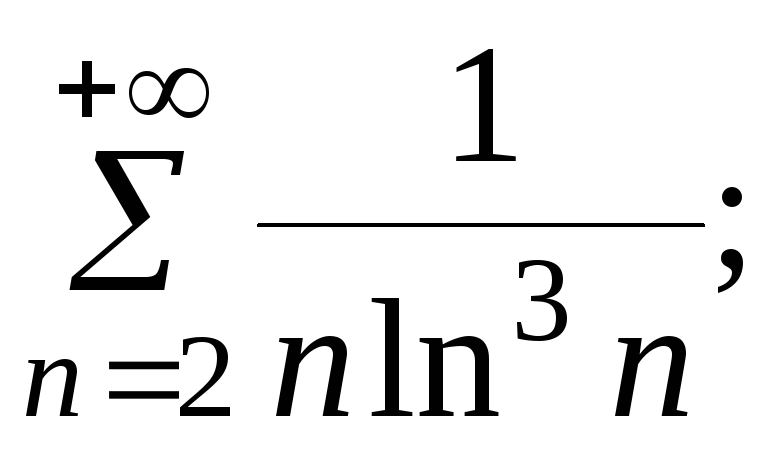
7.23.
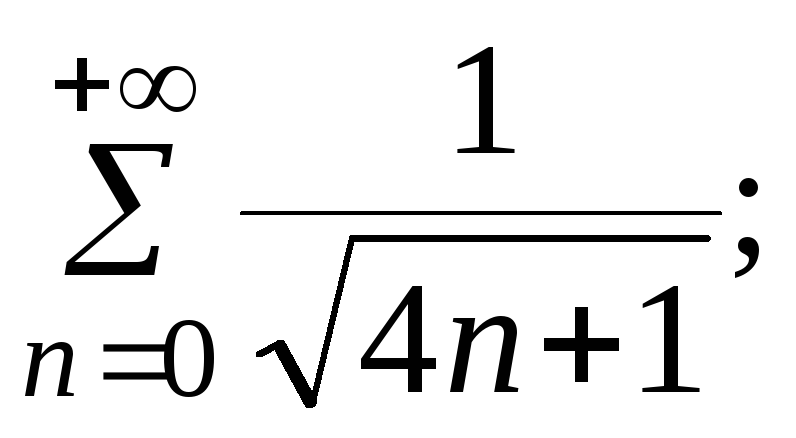 7.24.
7.24.

VIII. Решение дифференциальных уравнений
Обыкновенным дифференциальным уравнением называется уравнение
![]()
которое
связывает независимый аргумент x,
неизвестную функцию y
и ее производные
![]() Порядком
дифференциального уравнения называется
максимальный порядок производной,
входящей в уравнение.
Порядком
дифференциального уравнения называется
максимальный порядок производной,
входящей в уравнение.
Решением
дифференциального уравнения называется
функция
![]() ,
которая при подстановке в уравнение
превращает его в тождество. График этой
функции называетсяинтегральной
кривой.
,
которая при подстановке в уравнение
превращает его в тождество. График этой
функции называетсяинтегральной
кривой.
Уравнения с разделяющимися переменными
Дифференциальное уравнение вида:
![]()
называется уравнением с разделенными переменными. Уравнение, которое приводится к данному виду, называется дифференциальным уравнением с разделяющимися переменными.
Пример 8.1. Решить дифференциальное уравнение:
![]()
Решение.
![]()
![]()
![]()
![]()
![]()
Таким образом, получаем общий интеграл:
![]()
Однородные дифференциальные уравнения первого порядка
Дифференциальное уравнение вида:
![]()
где
![]() и
и![]() – однородные функции одинакового
измерения, называетсяоднородным
дифференциальным уравнением первого
порядка.
Данное уравнение можно привести к виду
– однородные функции одинакового
измерения, называетсяоднородным
дифференциальным уравнением первого
порядка.
Данное уравнение можно привести к виду
![]() где
где![]() – однородная функция нулевого измерения.
С помощью замены
– однородная функция нулевого измерения.
С помощью замены![]() где
где![]() – новая неизвестная функция,
рассматриваемое уравнение сводится
к уравнению с разделяющимися переменными.
– новая неизвестная функция,
рассматриваемое уравнение сводится
к уравнению с разделяющимися переменными.
Пример
8.2.
Решить дифференциальное уравнение:
![]()
Решение.
Сделаем замену
![]() и получим:
и получим:
![]()
![]()
![]()
![]() ;
;
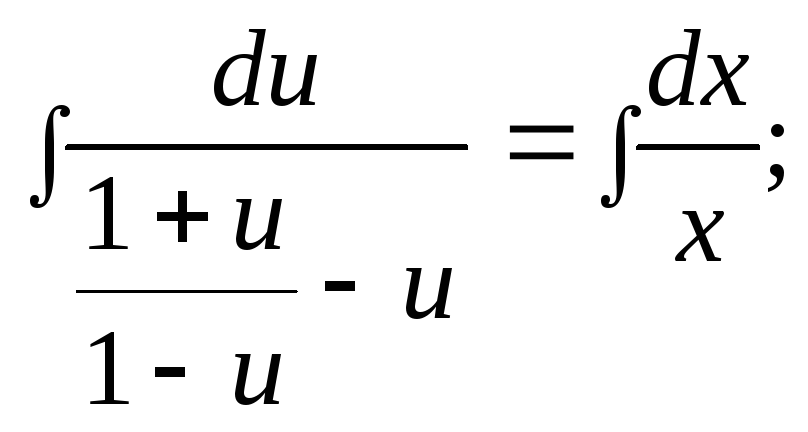
![]()
![]()
Сделав
обратную замену
![]() получим общий интеграл:
получим общий интеграл:
![]()
Линейные дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид
![]()
где
![]() и
и![]() – некоторые (непрерывные) функции
переменной
– некоторые (непрерывные) функции
переменной![]() .
В случае, когда функция
.
В случае, когда функция![]() тождественно равна нулю, уравнение
называетсяоднородным,
в противном случае – неоднородным.
тождественно равна нулю, уравнение
называетсяоднородным,
в противном случае – неоднородным.
Будем
искать решение в виде
![]() .
Очевидно, что здесь искомыми становятся
функции
.
Очевидно, что здесь искомыми становятся
функции![]() и
и![]() .
Так как
.
Так как![]() ,
то из определения следует
,
то из определения следует![]() или
или![]()
Найдем
сначала какое-либо частное решение
![]() уравнения
уравнения
![]()
Тогда
функция
![]() – решение уравнения
– решение уравнения
![]()
Таким образом, решение исходного уравнения сводится к решению двух уравнений с разделяющимися переменными.
Пример
8.3.
Решить уравнение
![]()
Решение.
Разделив
обе части уравнения на
![]() ,
получим линейное неоднородное уравнение:
,
получим линейное неоднородное уравнение:
![]()
Пусть
![]() ,
т.е.
,
т.е.![]() ,
тогда исходное уравнение примет вид
,
тогда исходное уравнение примет вид![]() или
или
![]()
Положим
![]() или
или![]() ,
откуда
,
откуда![]() .
Проинтегрировав, найдем какое-либо
частное решение этого уравнения,
например, при
.
Проинтегрировав, найдем какое-либо
частное решение этого уравнения,
например, при![]()
![]() и
и![]() .
При
.
При![]() равенство
равенство![]() обратится в уравнение
обратится в уравнение![]() ,
или
,
или![]() .
Решая данное уравнение с разделяющимися
переменными, получаем
.
Решая данное уравнение с разделяющимися
переменными, получаем![]() .
Тогда окончательно имеем:
.
Тогда окончательно имеем:
![]()
Уравнение Бернулли.
Уравнение вида
![]() где
где
![]()
![]()
называется
уравнением
Бернулли.
Данное уравнение приводится к линейному
с помощью подстановки
![]() .
Также можно использовать подстановку
.
Также можно использовать подстановку![]() или метод вариации произвольных
постоянных.
или метод вариации произвольных
постоянных.
Пример
8.4. Решить
дифференциальное уравнение
![]()
Решение.
Сделаем
замену
![]() и получим
и получим
![]()
Сгруппируем второе слагаемое с третьим:
![]() (
(![]() )
)
Приравняем
к нулю выражение в квадратных скобках
и найдем функцию
![]() :
:
![]()
Подставив
![]() в (
в (![]() ),
находим
),
находим![]() :
:
![]()
Отсюда
![]()
