2.54. 2.55.

2.56. 2.57.

2.58. 2.59.

2.60. 2.61.

2.62. 2.63.

2.64. 2.65.

2.66. 2.67.

2.68. 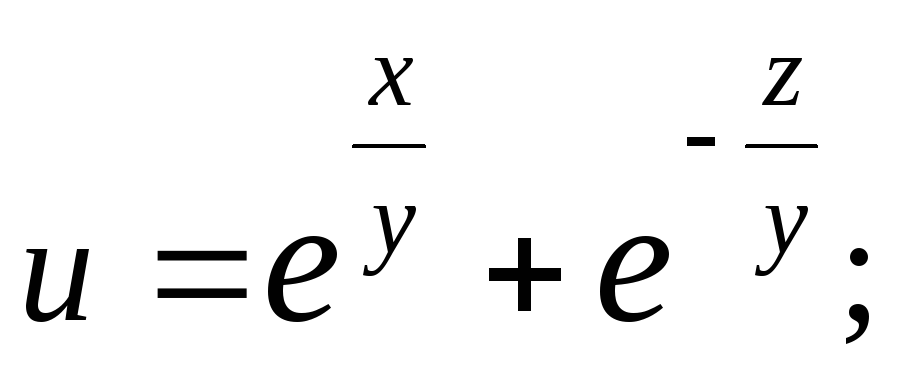2.69.

2.70. 2.71.

2.72. 2.73.

2.74. 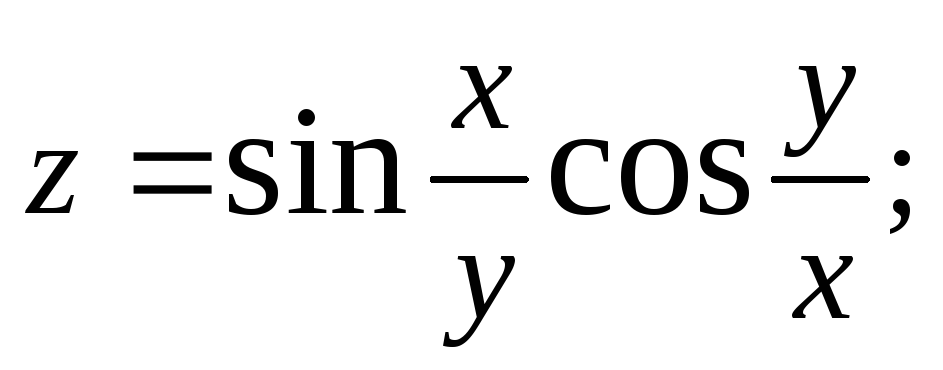2.75.

2.76. 2.77.

2.78. 2.79.

Пример 2.4. Показать, что функция удовлетворяет уравнению

Решение. Находим

(при постоянныхи);

(при постоянныхи);

(при постоянныхи).

Возводим полученные выражения в квадрат и подставляем в левую часть заданного уравнения:

Получаем тождественное равенство, т.е. функция u удовлетворяет заданному уравнению.

Показать, что данные функции удовлетворяют приведенным уравнениям:

2.80.

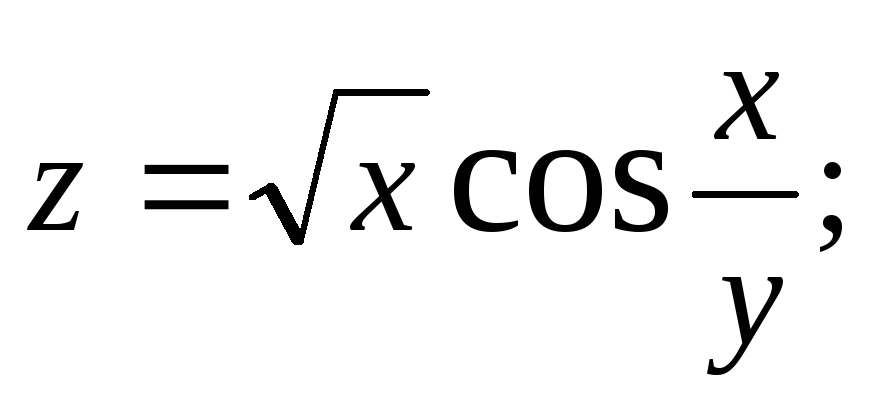
2.81.

2.82.

2.83.

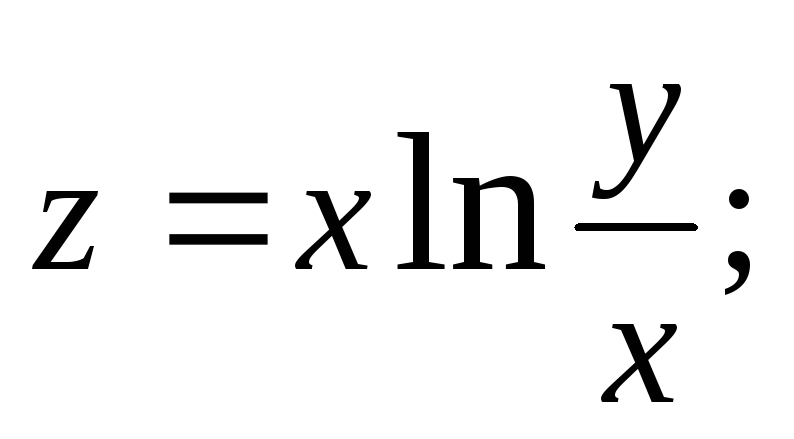
2.84.

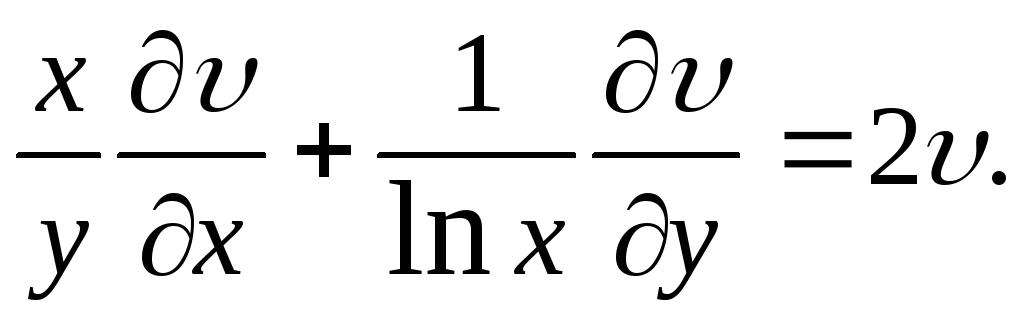
2.85.

Градиентом функции в точке называется вектор с началом в точке, координаты которого равны соответствующим частным производными, вычисленным в точке. Градиент обозначаетсяАналогично определяется градиент и для функции трех переменных.

Пример 2.5. Найти градиент функции в точкеМ(-2;3;-1).

Решение. Находим частные производные данной функции:

Вычисляем значение этих производных в точке М(-2;3;-1):

Окончательно получаем grad u(M)=(23; -35; -9).

Найти градиент функции:

2.86. в точке М(0; 3). 2.87. в точке М(1; 1).

2.88. в точке М(1; 1). 2.89. точке М(2; 0; 3).

2.90. в точке М(3; 2; 1).

2.91. в точке М(3; -1; 2).

2.92. точке М(a; b; c). 2.93. точке М(3; -1; 2).

III. Исследование функций и построение графиков

Схема исследования функций и построение их графиков:

1. Найти область определения функции.

2. Найти точки разрыва функции и ее односторонние пределы в этих точках.

3. Выяснить, не является ли функция четной, нечетной или периодической.

4. Найти точки пересечения графика функции с осями координат и интервалы знакопостоянства функции (необходимо решить уравнение ).

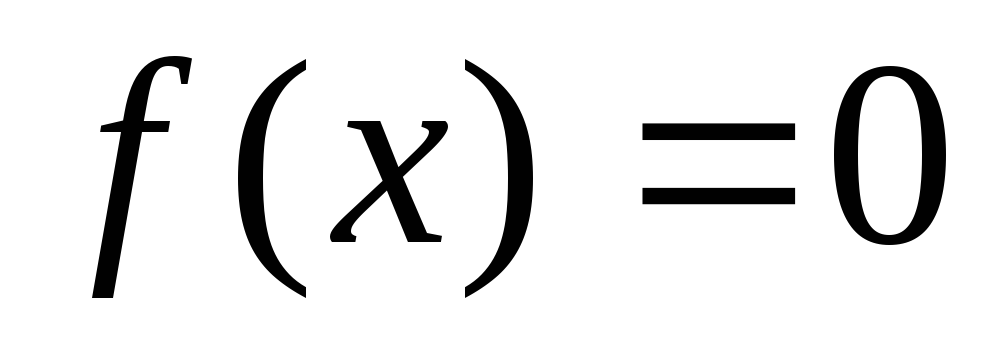5. Найти асимптоты графика функции:

- вертикальные;

- наклонные (горизонтальные).

6) Найти интервалы возрастания и убывания функции и точки экстремума.

7) Найти интервалы его выпуклости вверх и вниз и точки перегиба функции.

8) построить график функции, используя все полученные результаты исследования. Если их окажется недостаточно, то следует найти еще несколько точек графика функции исходя из её уравнения.

Пример 3.1. Исследовать функцию и построить её график:

1) Функция определена на всей числовой оси, кроме точки.

2) В точке функция имеет бесконечный разрыв: прии,. Во всех других точках числовой оси функция непрерывна.

3) Функция не является ни четной, ни нечетной, так как и,.

4) График функции пересекает ось Ox в точке (1,0) и не пересекает оси Oy.

5)Прямая (ось ординат) является вертикальной асимптотой графика функции, так как приона имеет бесконечный разрыв.

Следовательно, прямая есть наклонная асимптота. Припараметры и имеют те же значения, поэтому других асимптот нет.

6)

в точке , которая является критической;не существует в точке.

Исследуем критическую точку по знаку :

; ,

следовательно, есть точка минимума.

.

Слева от точки минимума, при ,, функция убывает; между точкой минимума и точкой разрыва, при,, функция возрастает; справа от точки разрыва, при,, функция убывает.

7) ;;не существует при, но это значениене может быть абсциссой точки перегиба, так как оно является точкой разрыва. Следовательно, график функции не имеет точек перегиба.

Во всей области определения функции , поэтому ее график всюду обращен выпуклостью вниз.

8) Используя все полученные данные, строим график функции.

y

1

x

0

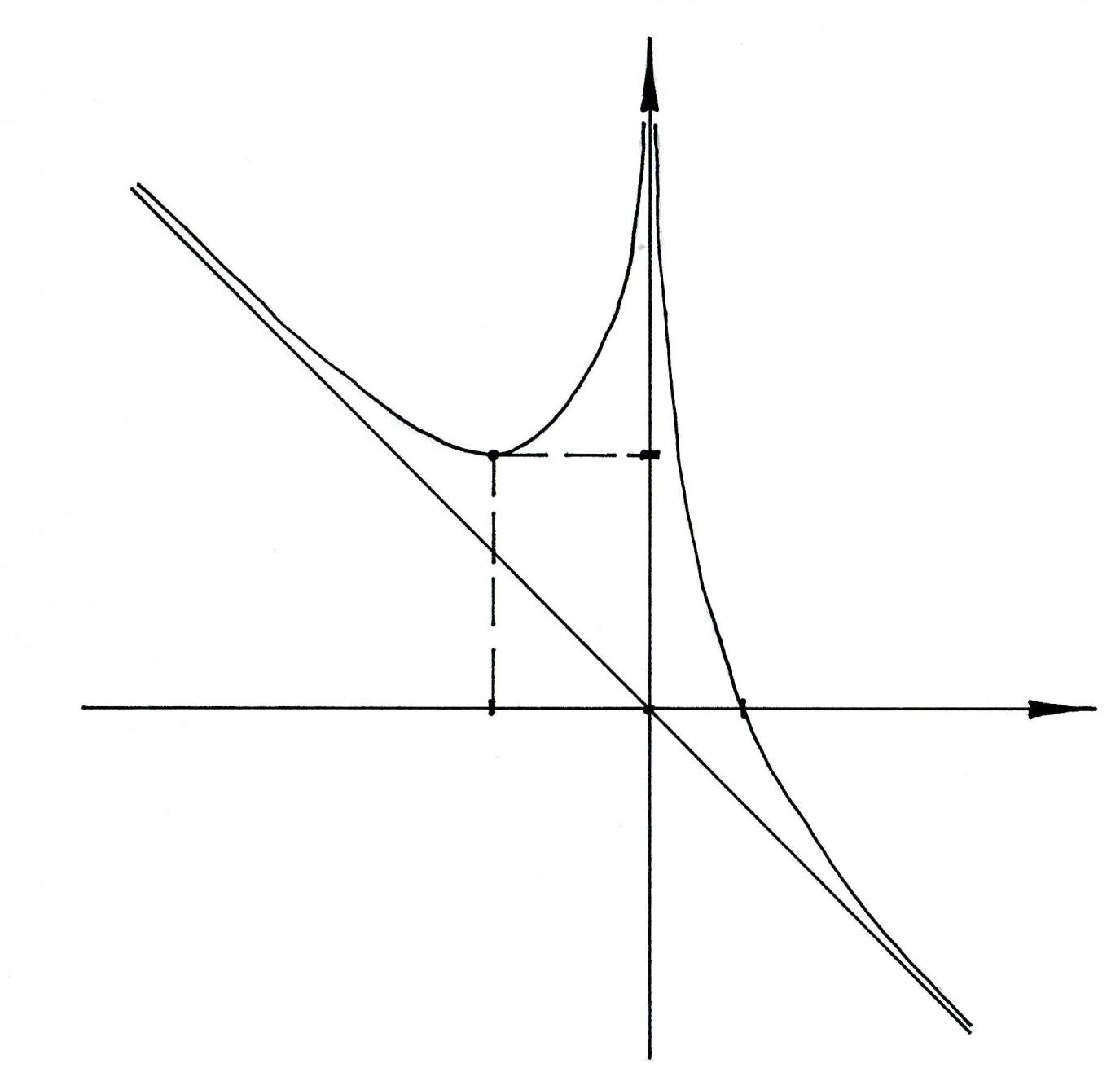
Пример 3.2. Исследовать и построить график функции .

1) Функция существует всюду, кроме точек .

2) В точках функция имеет бесконечный разрыв, причем:

3) Функция является четной, так как . Следовательно, ее график симметричен относительно осиOy.

4) Кривая проходит через начало координат, так как при . Других точек пересечения с координатными осями нет.

5) Прямые иявляются вертикальными асимптотами графика функции.

При имеем,

Таким образом, расстояние от любой точки М на кривой до прямой пристремится к нулю, следовательно, прямаяявляется горизонтальной асимптотой для данной кривой.

6) Находим производную ;

в точке .

При ,, функция убывает; при,, функция возрастает, следовательно,есть точка минимума.

Используя все полученные данные, строим график функции.

x
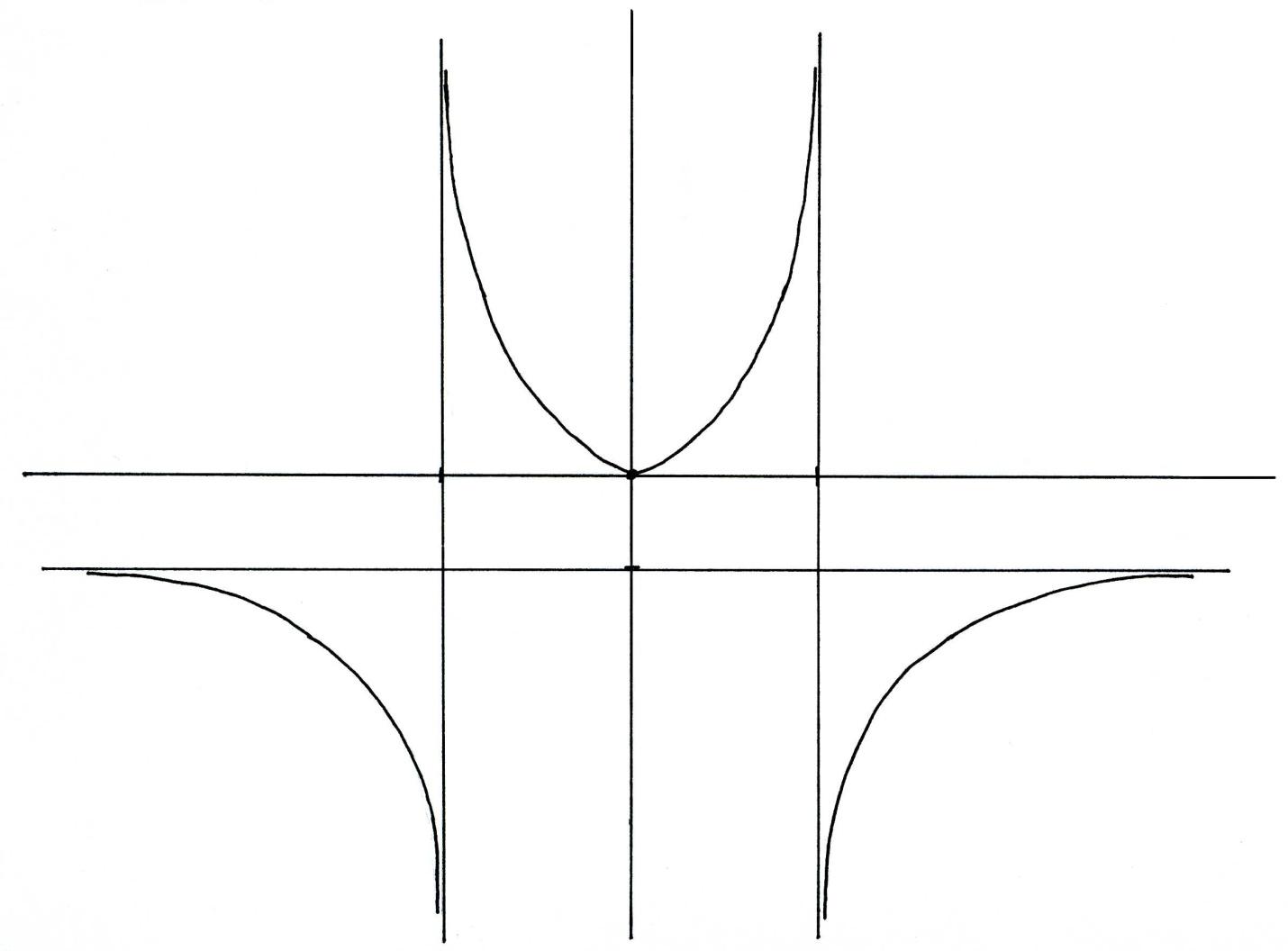