Вычисление площади поверхности вращения

Пример 6.2. Найти площадь поверхности, образованной вращением вокруг оси : дуги кубической параболызаключенной между прямымии

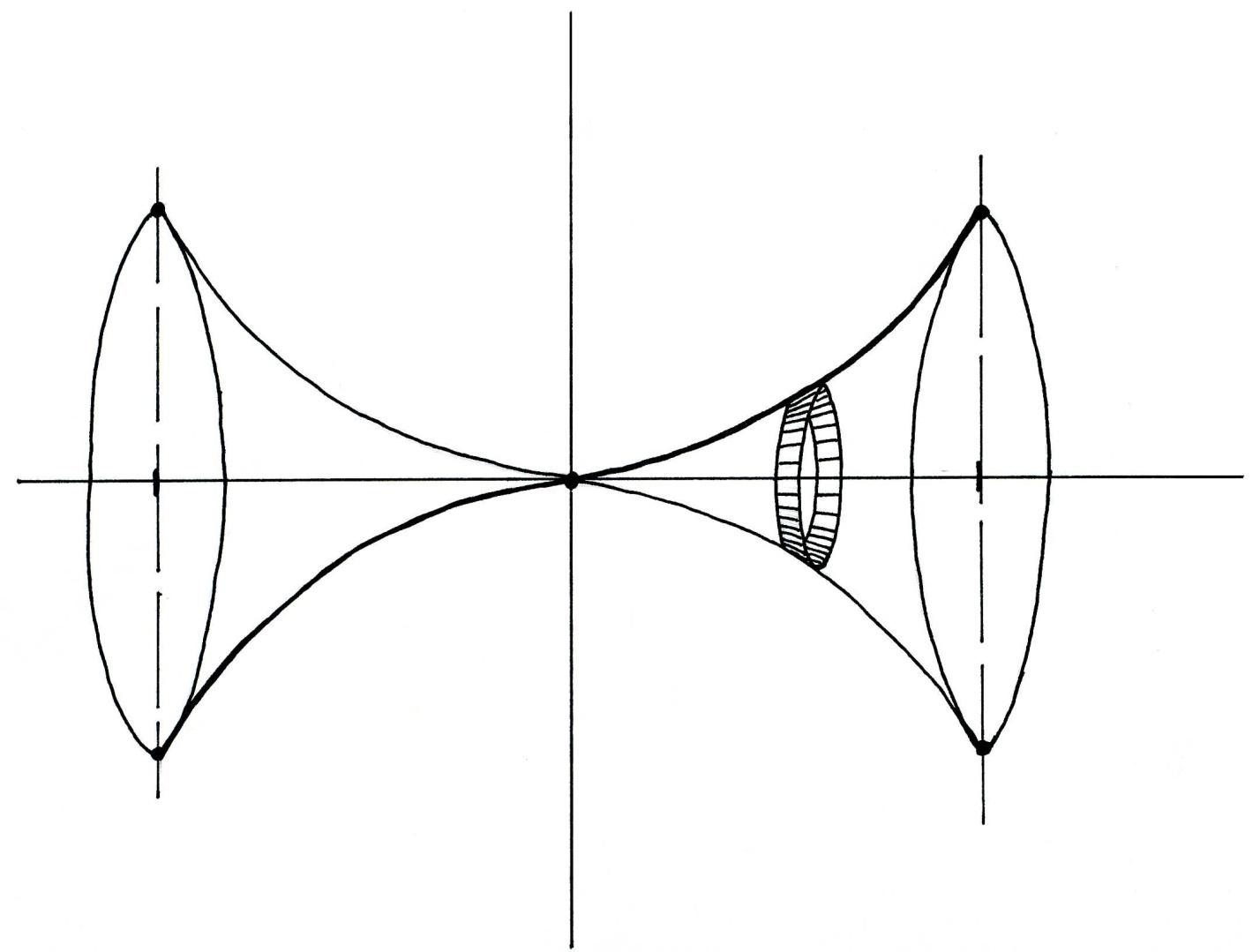
Поверхность, образуемая вращением дуги АВ вокруг оси , состоит из одинаковых частей. Поэтому, и согласно формуле:

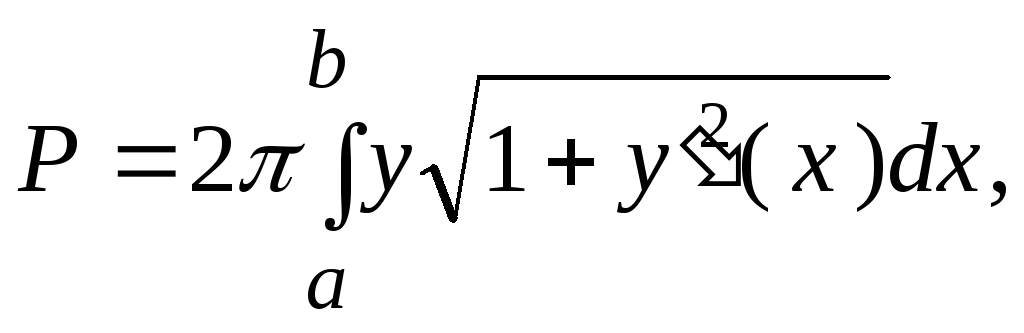
имеем

y

x

B

A

Вычислить площадь поверхности, образованной вращением

вокруг оси Ox:

6.16. Дуги параболы между точками пересечения с прямой.

6.17. Одной волны синусоиды .

6.18. Дуги кубической параболы от начала координат до.

6.19. Параболы от начала координат до.

6.20. Дуги , отсеченной прямой.

Вычисление объема тела вращения

Пример 6.3. Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной параболойи прямой.

Решение. Построив параболу и прямую, получим параболический сегмент. При вращении его вокруг оси образуется сегмент параболоида вращения.

y

x

A

B

a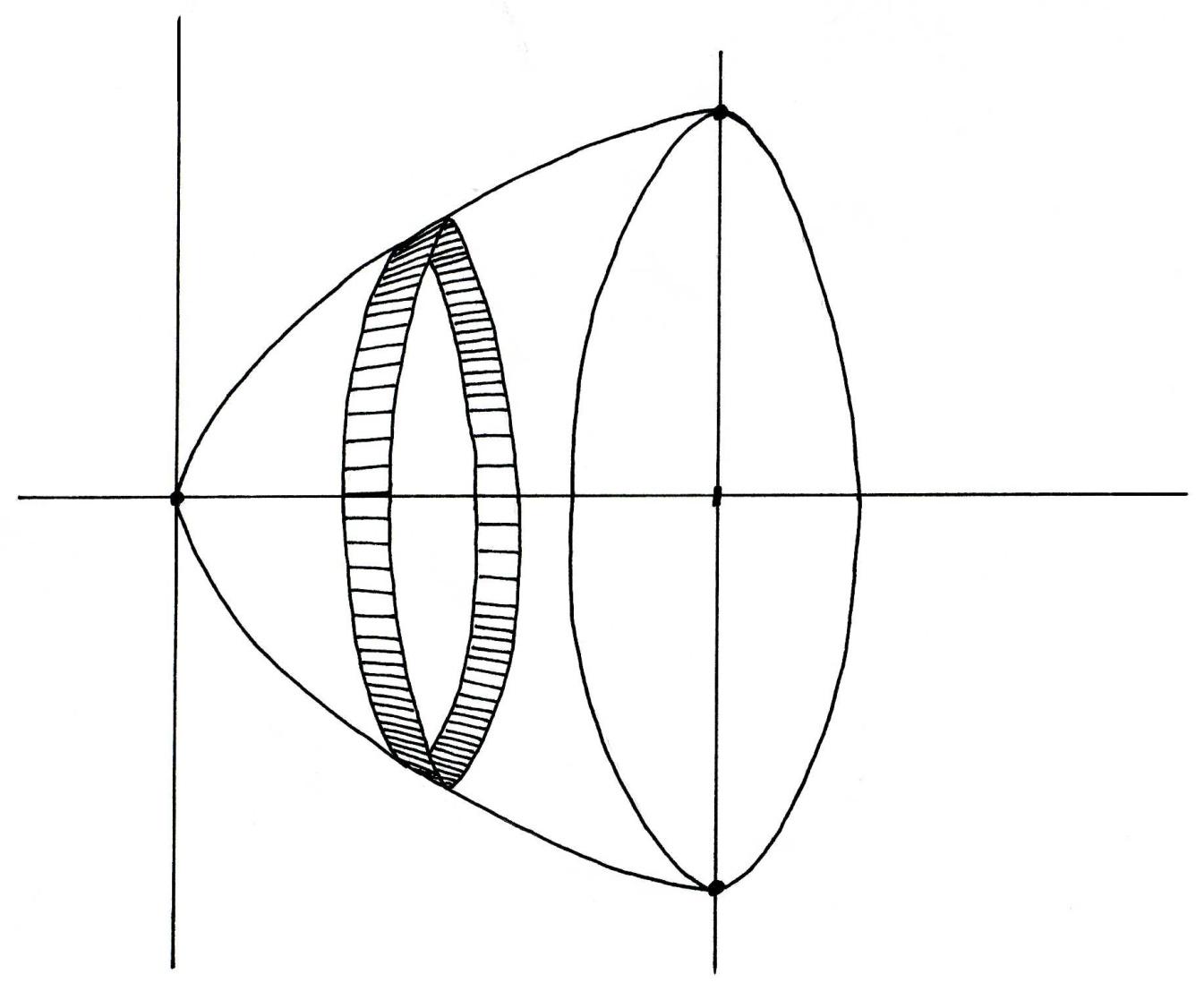

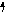
Объем полученного тела находим по формуле:

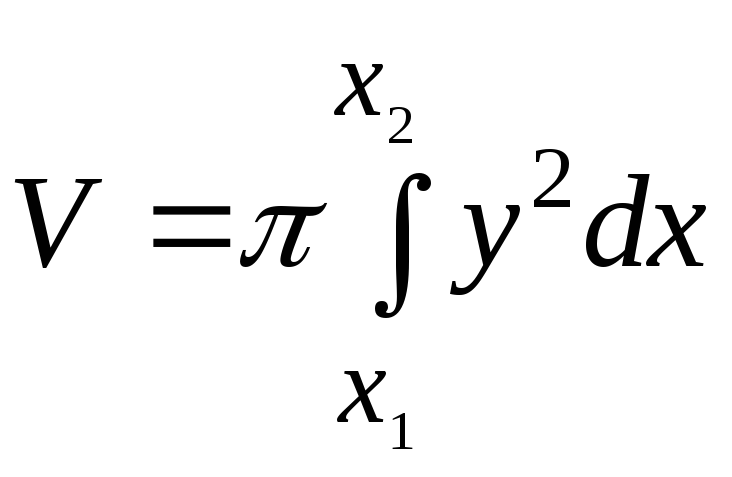
Найти объем тела, образованного вращением фигуры, ограниченной линиями:

6.21. вокруг оси.

6.22. вокруг оси.

6.23. вокруг прямой

6.24. (одной волной),вокруг оси.

6.25. вокруг оси.

6.26. вокруг оси.

6.27. вокруг оси.

6.28. вокруг прямой.

6.29. вокруг оси.

6.30. вокруг оси.

6.31. вокруг оси.

6.32. вокруг оси.

6.33. вокруг оси.

Понятие несобственного интеграла

Несобственным интегралом от функциина полуинтерваленазывается предел функциипри, стремящемся к, т.е.

Если предел, стоящий в правой части равенства, существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае – расходящимся. Работая с несобственными интегралами, обычно выделяют две задачи:

- исследование вопроса о сходимости заданного несобственного интеграла;

- вычисление значения интеграла в случае, если он является сходящимся.

Пример 6.4. Вычислить

Решение. По определению

Для нахождения интеграла, стоящего под знаком предела, используем формулу Ньютона – Лейбница:

Тогда

Таким образом, искомый несобственный интеграл сходится к 1.

Если рассматривать несобственный интеграл на интервале , то его можно представить как сумму двух интегралов, т.е.

Если интегралы, входящие в правую часть равенства, сходятся, то рассматриваемый интеграл называется сходящимся, а если хотя бы один из интегралов правой части расходится, то – расходящимся.

Пример 6.5. Вычислить

Представим интеграл в виде суммы двух интегралов и исследуем их на сходимость, полагая .

т.е. первый интеграл сходится к 1.

т.е. второй интеграл расходится, а, следовательно, расходящимся будет и несобственный интеграл

Вычислить несобственные интегралы (или установить их расходимость):

6.34. 6.35.

6.36. 6.37.

6.38. 6.39.

6.40. 6.41.

6.42. 6.43.

6.44. 6.45.

6.46. 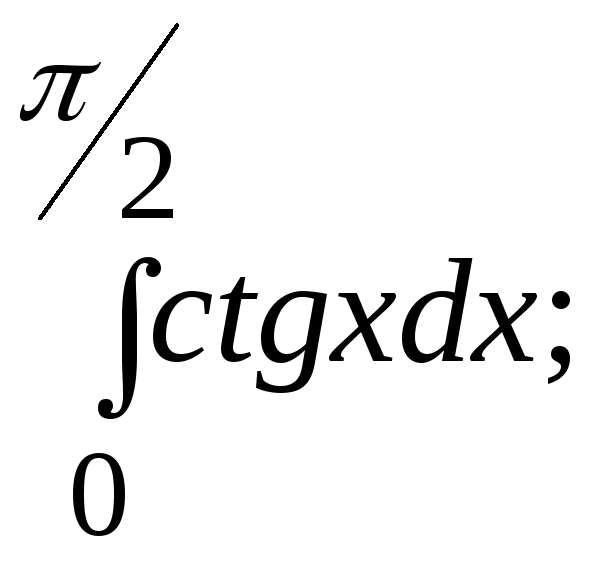6.47.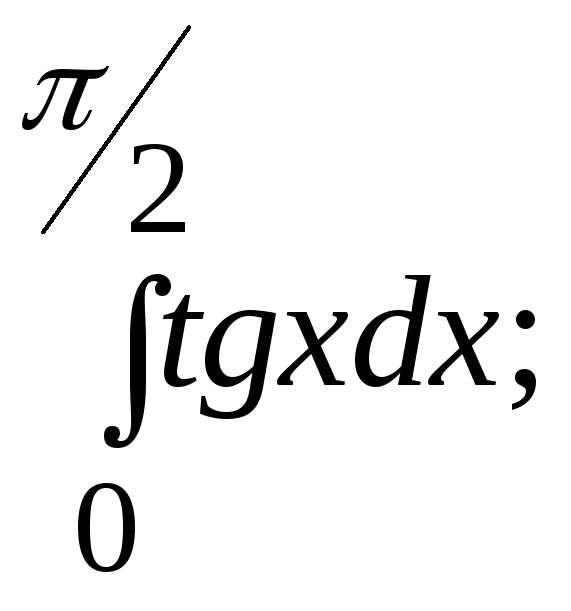

6.48. 6.49.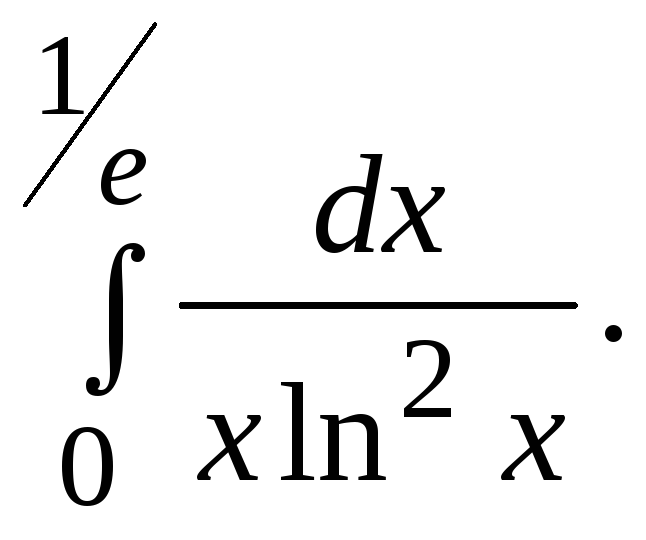

VII. Исследование на сходимость числовых рядов

Общие признаки сходимости ряда:

1. Критерий Коши сходимости числового ряда. Для того, чтобы ряд сходился, необходимо и достаточно, чтобы для любогонашелся номер, такой, что для любыхвыполнялось условие.

2. Необходимое условие сходимости ряда.

Если ряд сходится, то его общий член стремится к нулю, т.е..

Признаки сходимости знакоположительных рядов

Ряд в котором всеназывается знакоположительным.

Общий признак сходимости знакоположительных рядов

Для того, чтобы знакоположительный ряд сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху.

Признаки сравнения знакоположительных рядов

Пусть даны два знакоположительных ряда иТогда:

1) если при всехто из сходимости рядаследует сходимость рядаа из расходимости рядаследует расходимость ряда

2) если существует 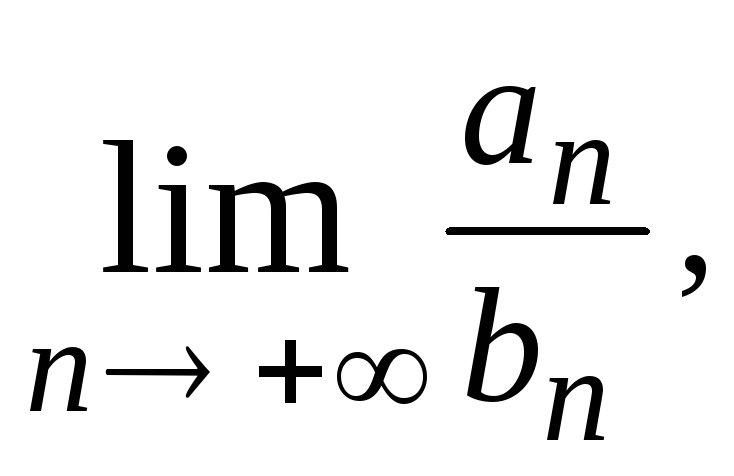не равный нулю и конечный, то рядыисходятся и расходятся одновременно;

3) если при всех, то из сходимости рядавытекает сходимость рядаа из расходимости рядавытекает расходимость ряда

Признак Коши

Пусть для знакоположительного ряда существует пределТогда:

а) если то рядсходится;

б) если то рядрасходится;

Примечание. Если то теорема не дает ответа на вопрос о сходимости ряда.

Признак Даламбера

Пусть для знакоположительного ряда существует пределТогда справедливы следующие утверждения:

а) если , то рядсходится;

б) если , то рядрасходится.

Примечание. Теорема не дает ответа на вопрос о сходимости ряда, если

Интегральный признак Коши

Пусть члены ряда положительны и убывают, т.е.и пусть- непрерывная положительная убывающая функция, определенная притакая, что

тогда интеграл и рядсходятся или расходятся одновременно.

Пример 7.1. Исследовать по признаку Даламбера сходимость ряда

Решение. Зная, -й член ряда, находим следующий за ним ()-й член, заменяя в выражении-го членачерез (). Затем ищем предел отношения последующего членак предыдущемупри неограниченном возрастании

Здесь, следовательно, согласно признаку Даламбера данный ряд сходится.

Пример 7.2. Исследовать по признаку Коши сходимость ряда

Решение.

Здесь следовательно, согласно признаку Коши данный ряд сходится.

Пример 7.3. Исследовать по признаку сравнения сходимость ряда:

Решение. Сравним данный ряд с гармоническим рядом:

Каждый член данного ряда, начиная со второго, больше соответствующего членагармонического ряда:и, так как гармонический ряд расходится, то, согласно признаку сравнения, данный ряд также расходится.

Пример 7.4. Исследовать по признаку сравнения сходимость ряда:

Решение. Сравним данный ряд с бесконечной геометрической прогрессией: , которая представляет сходящийся ряд. Каждый член исследуемого ряда, начиная с третьего, меньше соответствующего членабесконечной геометрической прогрессии:

следовательно, согласно признаку сравнения, исследуемый ряд является сходящимся.

Пример 7.5. Исследовать по интегральному признаку сходимость ряда:

Решение. Заменяем в заданном выражении общего члена ряда номернепрерывной переменнойи убеждаемся, что полученная функцияявляется непрерывной и убывающей во всем бесконечном интервале изменения. Затем находим несобственный интеграл отс бесконечным верхним пределом.

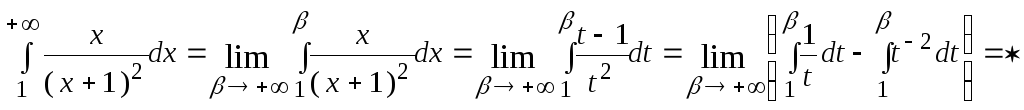
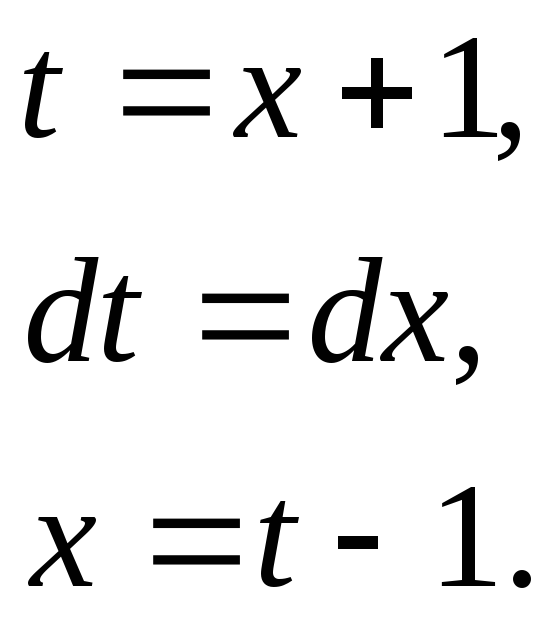
Здесь несобственный интеграл расходится. Следовательно, согласно интегральному признаку, и данный ряд также расходится.

Исследовать на сходимость следующие ряды: