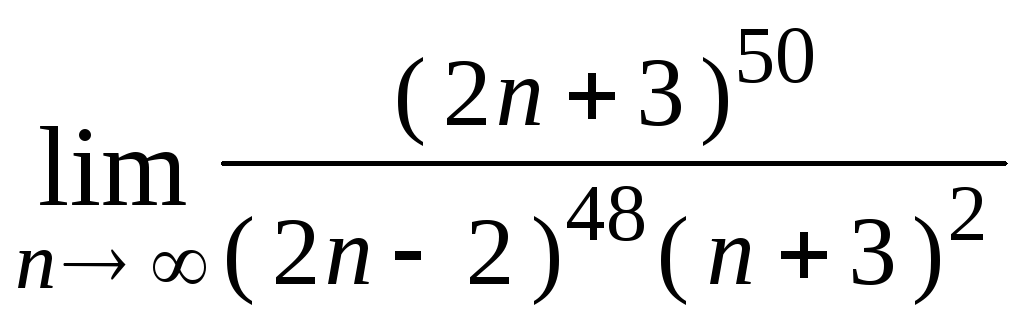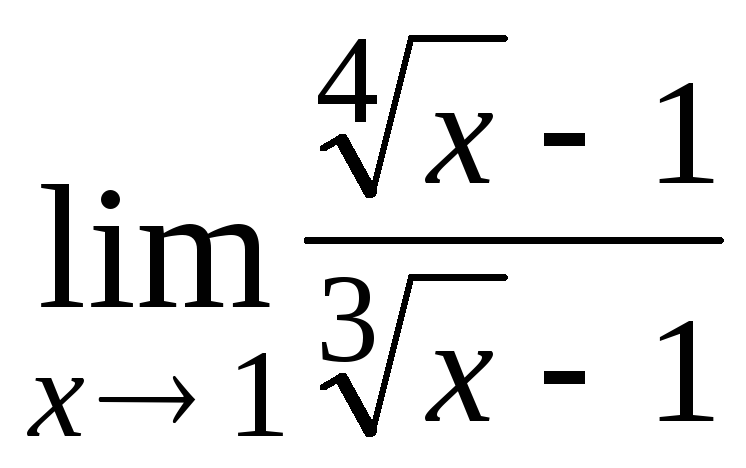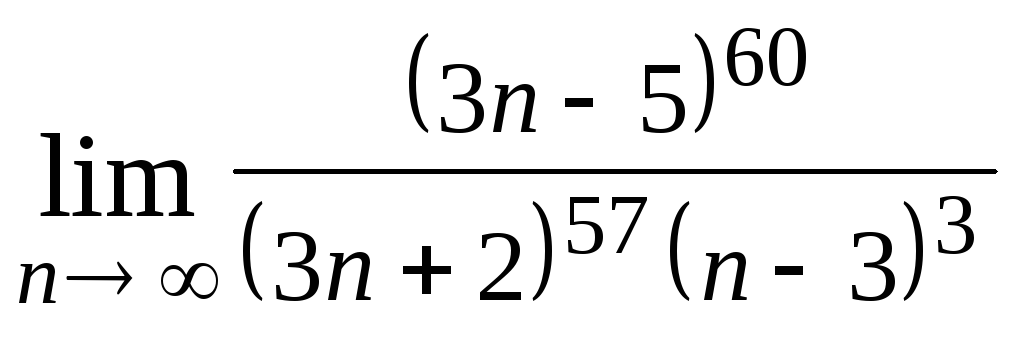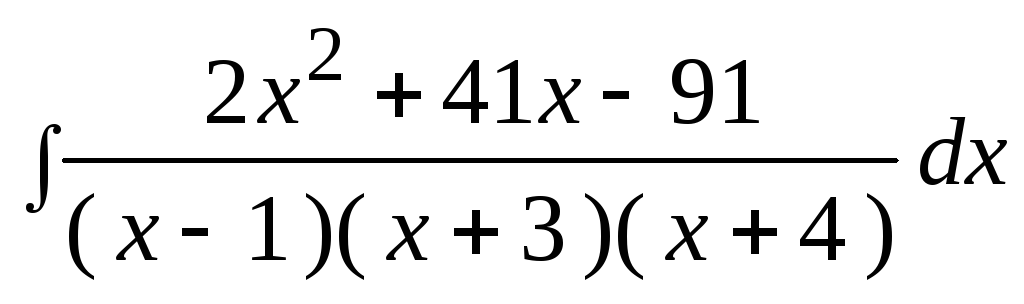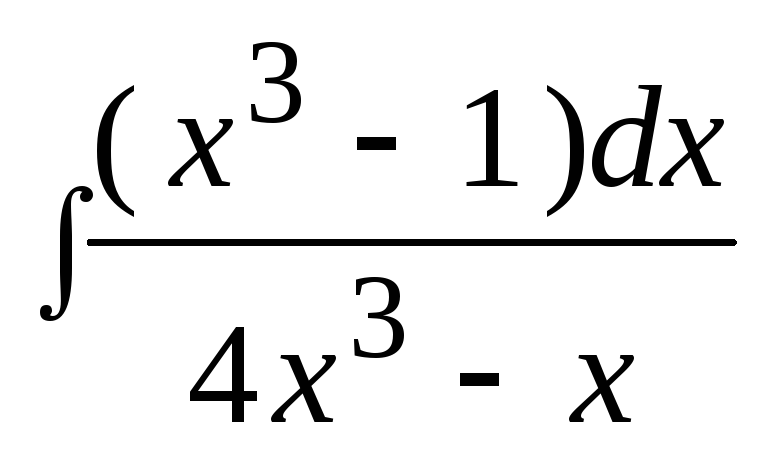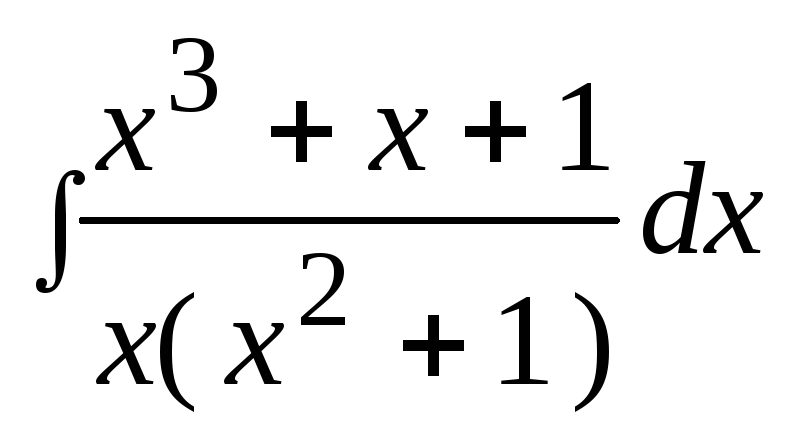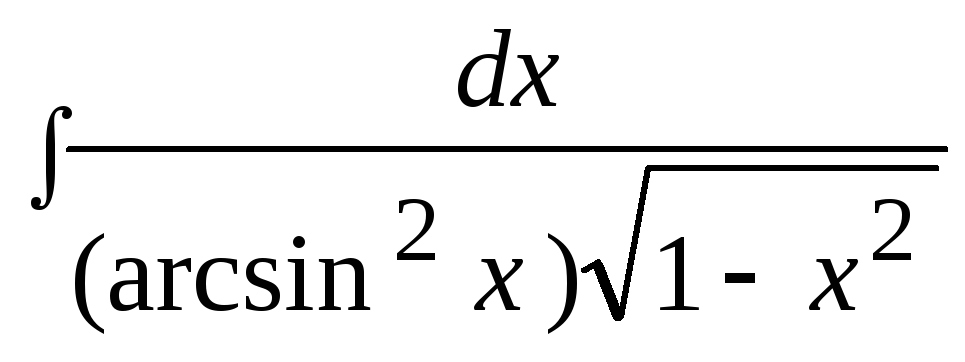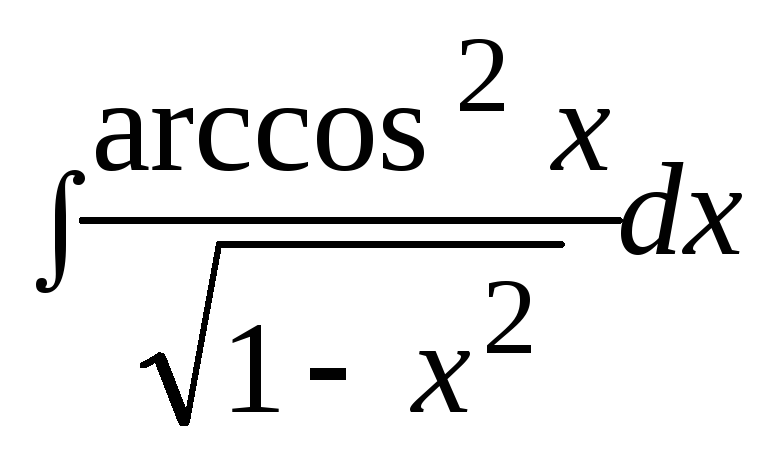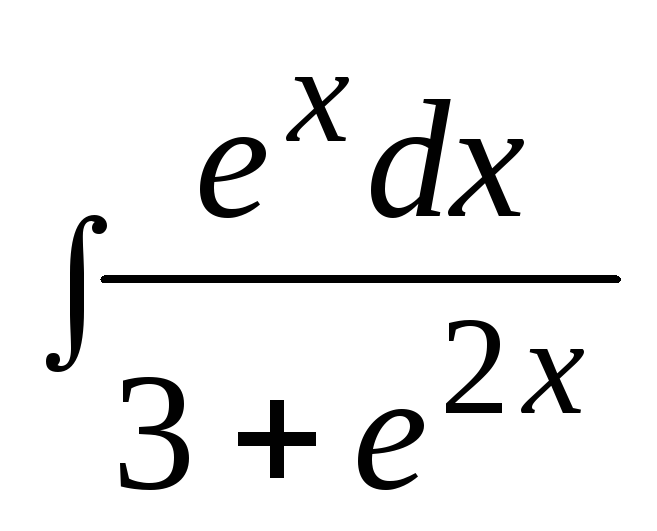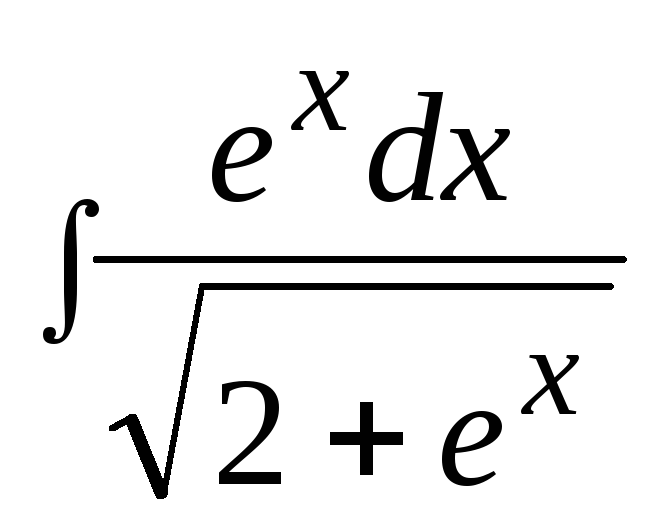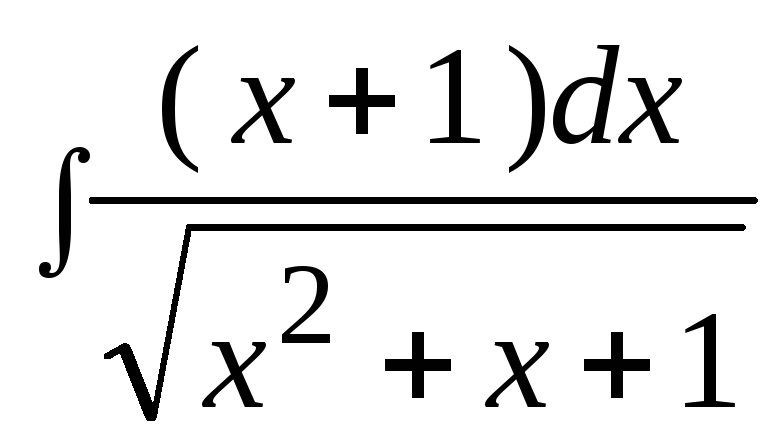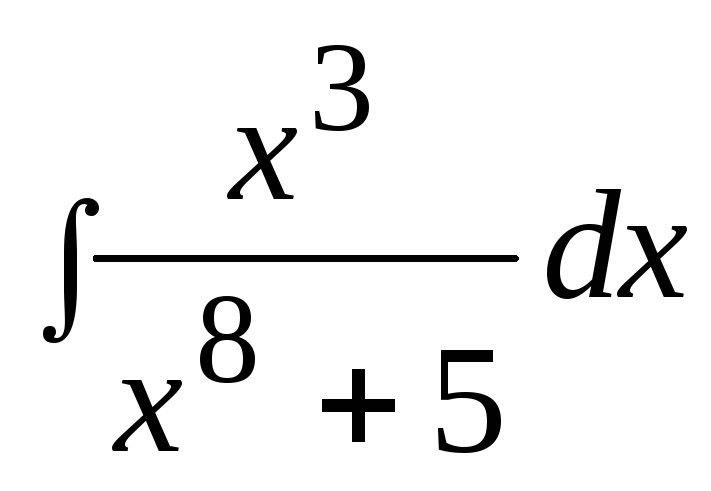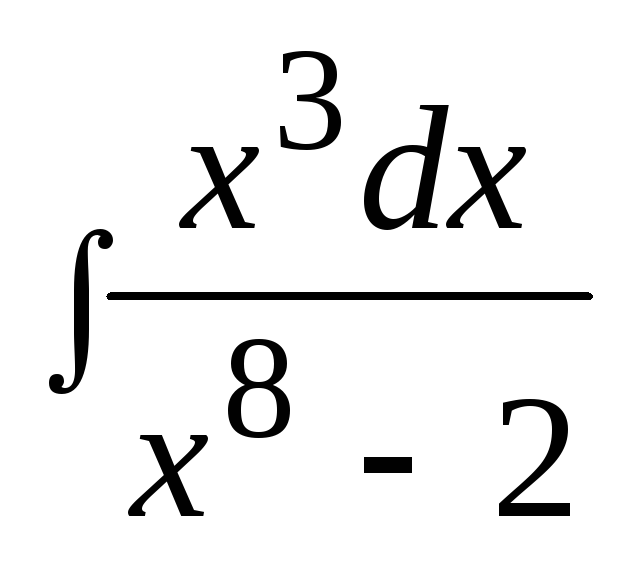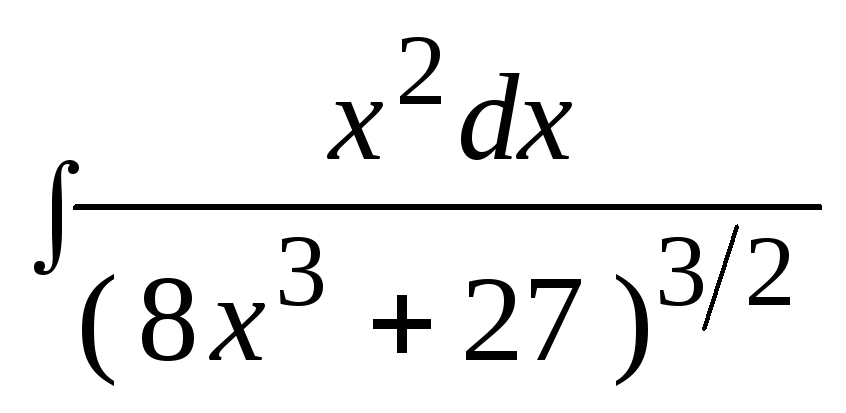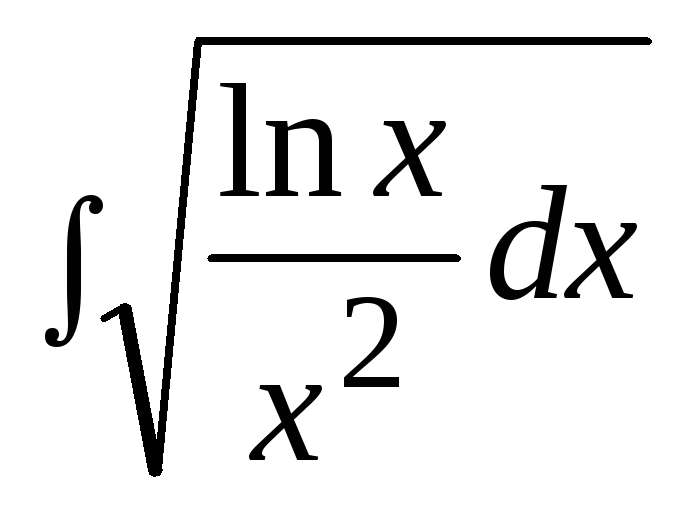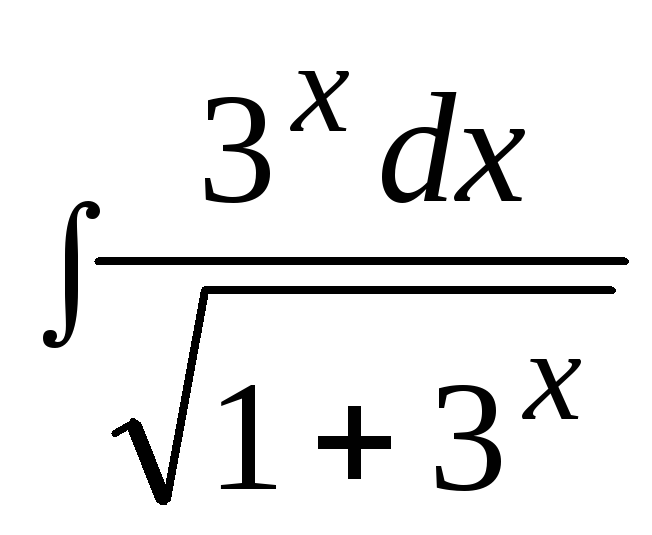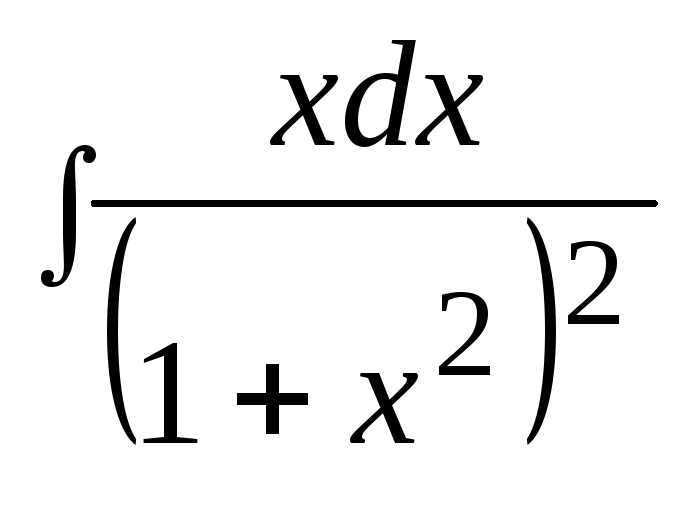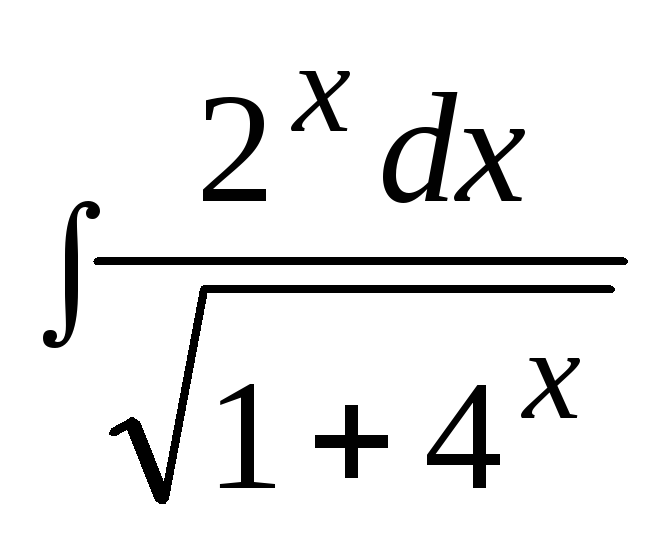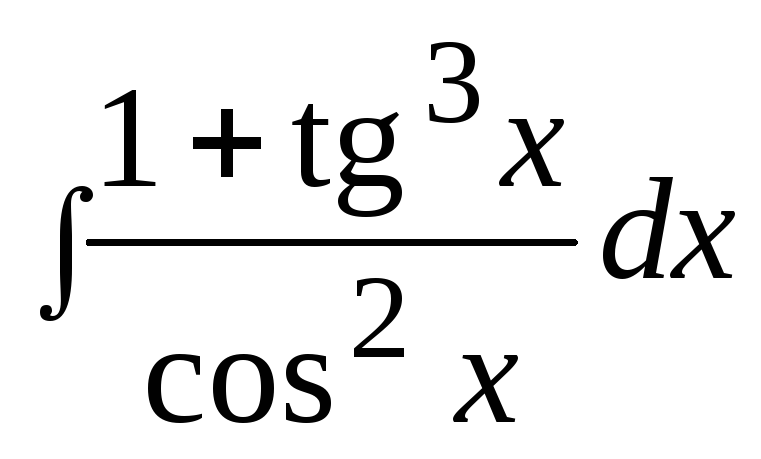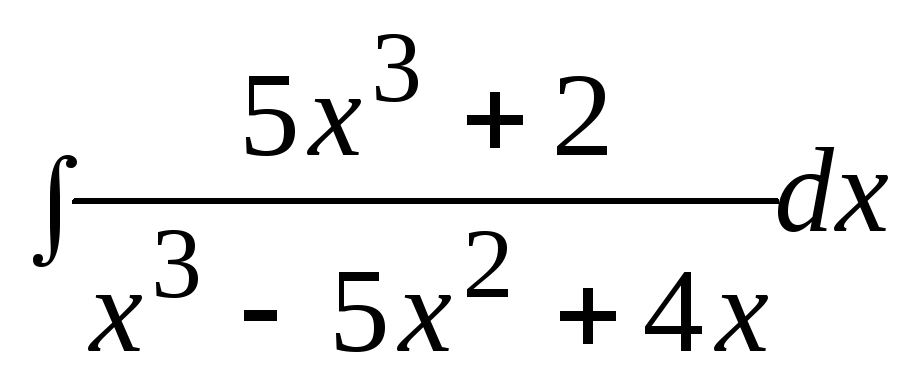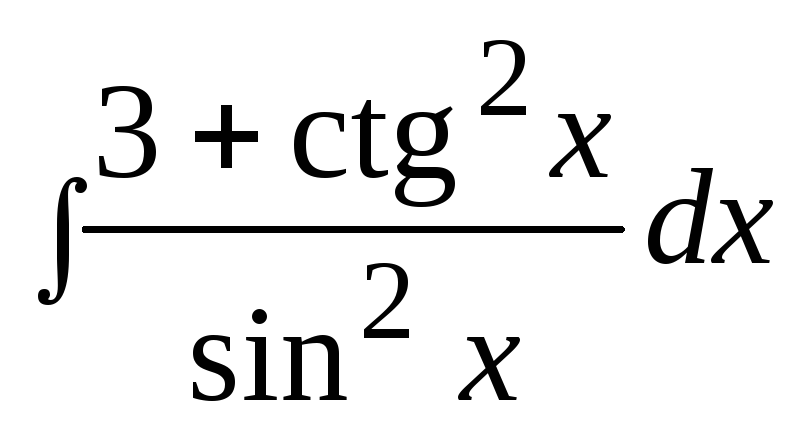Уравнения высших порядков, допускающие понижение порядка
Уравнение
n-го
порядка
решается последовательным интегрированием.
Умножая
обе его части на
и интегрируя, получаем уравнение
–го
порядка:
Снова
умножая обе части на
и интегрируя, получаем уравнение
–го
порядка:
и т.д.
Пример
8.5.
Решить дифференциальное уравнение
Решение. Проинтегрируем данное уравнение 4 раза:
Решить дифференциальные уравнения:
8.1.
где
-
постоянная
8.2.
8.3.
8.4.
8.5.
8.6.
8.7.
8.8.
8.9.
8.10.
8.11.
8.12.
8.13.
8.14.
8.15.
8.16.
8.17.
8.18.
8.19.
8.20.
8.21.
8.22.
8.23.
8.24.
8.25.
8.26.
8.27.
8.28.
8.29.
8.30.
8.31.
8.32.
8.33.
8.34.
8.35.
8.36.
8.37.
при
условии
8.38.
8.39.
8.40.
при
условии
8.41.
8.42.
8.43.
если
8.44.
если
8.45.
если
Варианты контрольных заданий
1. Вычислить предел функции:
|
Вариант |
Предел |
Вариант |
Предел |
|
1 |
|
16 |
|
|
2 |
|
17 |
|
|
3 |
|
18 |
|
|
4 |
|
19 |
|
|
5 |
|
20 |
|
|
6 |
|
21 |
|
|
7 |
|
22 |
|
|
8 |
|
23 |
|
|
9 |
|
24 |
|
|
10 |
|
25 |
|
|
11 |
|
26 |
|
|
12 |
|
27 |
|
|
13 |
|
28 |
|
|
14 |
|
29 |
|
|
15 |
|
30 |
|
2. Исследовать функцию и построить её график:
|
Вариант |
Функция |
Вариант |
Функция |
|
1 |
|
16 |
|
|
2 |
|
17 |
|
|
3 |
|
18 |
|
|
4 |
|
19 |
|
|
5 |
|
20 |
|
|
6 |
|
21 |
|
|
7 |
|
22 |
|
|
8 |
|
23 |
|
|
9 |
|
24 |
|
|
10 |
|
25 |
|
|
11 |
|
26 |
|
|
12 |
|
27 |
|
|
13 |
|
28 |
|
|
14 |
|
29 |
|
|
15 |
|
30 |
|
3. Найти неопределенный интеграл:
|
Вариант |
Интеграл |
Вариант |
Интеграл |
|
1 |
|
16 |
|
|
2 |
|
17 |
|
|
3 |
|
18 |
|
|
4 |
|
19 |
|
|
5 |
|
20 |
|
|
6 |
|
21 |
|
|
7 |
|
22 |
|
|
8 |
|
23 |
|
|
9 |
|
24 |
|
|
10 |
|
25 |
|
|
11 |
|
26 |
|
|
12 |
|
27 |
|
|
13 |
|
28 |
|
|
14 |
|
29 |
|
|
15 |
|
30 |
|
4. Вычислить площадь фигуры, ограниченной линиями:
|
Вариант |
Уравнения линий |
Вариант |
Уравнения линий |
|
1 |
|
16 |
|
|
2 |
|
17 |
|
|
3 |
|
18 |
|
|
4 |
|
19 |
|
|
5 |
|
20 |
|
|
6 |
|
21 |
|
|
7 |
|
22 |
|
|
8 |
|
23 |
|
|
9 |
|
24 |
|
|
10 |
|
25 |
|
|
11 |
|
26 |
|
|
12 |
|
27 |
|
|
13 |
|
28 |
|
|
14 |
|
29 |
|
|
15 |
|
30 |
|
