Исследовать функции и построить их графики:

3.1. 3.2.

3.3. 3.4.

3.5. 3.6.

3.7. 3.8.

3.9. 3.10.

3.11. 3.12.

3.13. 3.14.

3.15. 3.16.

3.17. 3.18.

3.19. 3.20.

3.21. 3.22.

3.23. 3.24.

3.25. 3.26.

3.27. 3.28.

3.29.3.30.

3.31. 3.32.

3.33. 3.34.

3.35. 3.36.

3.37. 3.38.

3.39. 3.40.

IV. Вычисление неопределенных интегралов

Таблица основных интегралов:

1) 2)

3) 4)

5)

6) в частности,

7) 8)

9)10)

11) 12)

Метод непосредственного интегрирования

Пример 4.1.

Пример 4.2.

Так как , то

Метод замены переменной

Пример 4.3.

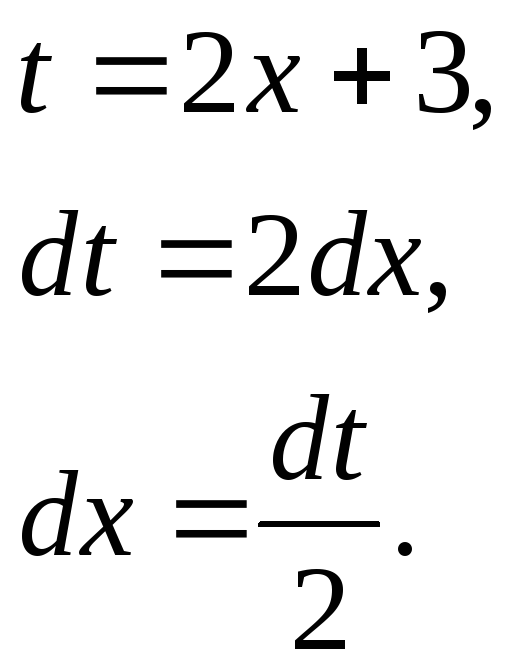
Пример 4.4.

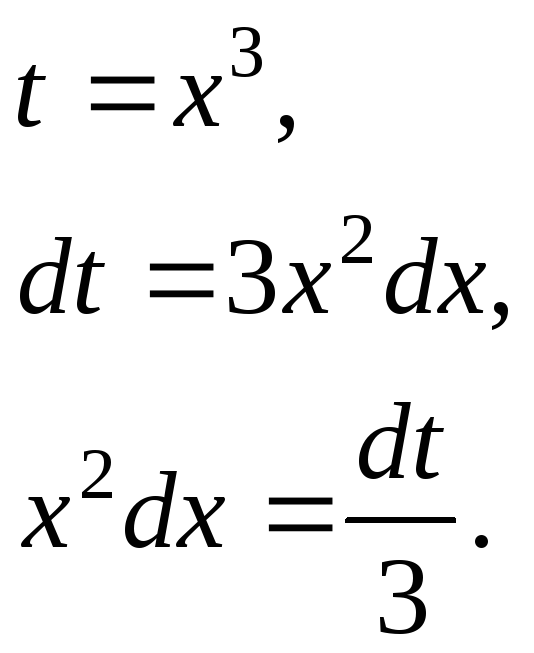
Метод интегрирования по частям

Формула интегрирования по частям:

где и- функции дифференцируемые от.

Пример 4.5.

,

Формулу интегрирования по частям можно применять последовательно несколько раз.

Пример 4.6.

Пример 4.7.

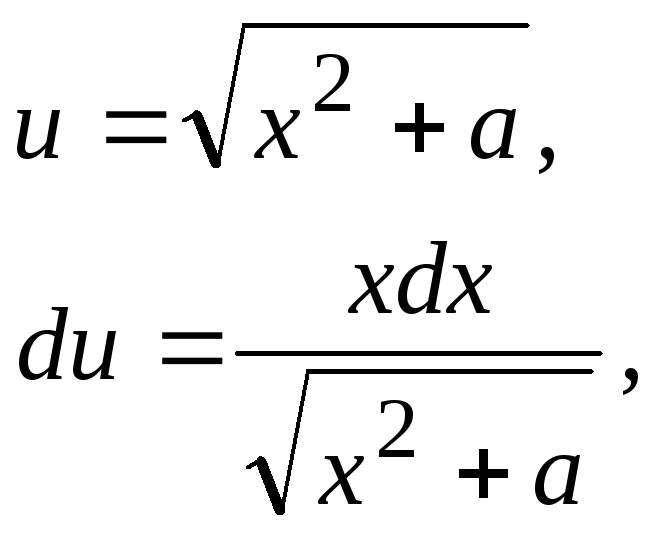
Вычислим интеграл:

Подставляя полученный результат в предыдущее равенство, получим:

Объединим оба интеграла в левой части:

Окончательно получим:

Вычислить следующие интегралы и проверить результат дифференцированием:

4.1. 4.2.

4.3. 4.4.

4.5.4.6.

4.7. 4.8.

4.9. 4.10.

4.11. 4.12.

4.13. 4.14.

4.15. 4.16.

4.17. 4.18.

4. 19. 4.20.

4.21. 4.22.

4.23. 4.24.

4.25. 4.26.

4.27. 4.28.

4.29.4.30.

4.31. 4.32.

4.33. 4.34.

4.35. 4.36.

4.37. 4.38.

4.39. 4.40.

4.41. 4.42.

4.43. 4.44.

4.45. 4.46.

4.47. 4.48.

4.49. 4.50.

4.51.4.52.

4.53. 4.54.

4.55. 4.56.

4.57. 4.58.

4.59. 4.60.

4.61. 4.62.

4.63. 4.64.

4.65.4.66.

4.67. 4.68.

4.69. 4.70.

4.71. 4.72.

4.73. 4.74.

4.75. 4.76.

4.77. 4.78.

4.79. 4.80.

4.81. 4.82.

4.83. 4.84.

4.85. 4.86.

4.87. 4.88.

4.89. 4.90.

4.91. 4.92.

4.93. 4.94.

4.95. 4.96.

4.97. 4.98.

V. Вычисление определенного интеграла

Формула Ньютона – Лейбница

Теорема. Пусть функция непрерывна на отрезкеи- любая первообразная дляна. Тогда определенный интеграл от функциинаравен приращению первообразнойна этом отрезке, т.е.

Нахождение определенных интегралов с помощью формулы Ньютона – Лейбница осуществляется в два этапа: 1) используя методы вычисления неопределенного интеграла, находят некоторую первообразную F(x) для подынтегральной функции f(x); 2) применяя собственно формулу Ньютона – Лейбница, находят приращение первообразной, равное искомому интегралу.

Пример 5.1. Вычислить

Формула замены переменной в определенном интеграле

Теорема. Пусть функция имеет непрерывную производную на отрезке,,и функциянепрерывна в каждой точкевида, где.

Тогда справедливо следующее равенство:

Пример 5.2. Вычислить

Положим ТогдаиЕсли, тои если, то. Следовательно,

Формула интегрирования по частям для определенного интеграла

Теорема. Пусть функции иимеют непрерывные производные на отрезке. Тогда

где

Пример 5.3. Вычислить

Пусть ,. ТогдаиПрименяя формулу интегрирования по частям, получаем

Полученный интеграл находим методом замены переменной. Пусть , тогда,и если, то, если, то. Следовательно,

Вычислить определенные интегралы:

5.1. 5.2.

5.3. 5.4.

5.5. 5.6.

5.7. 5.8.

5.9. 5.10.

5.11. 5.12.

5.13. 5.14.

5.15. 5.16.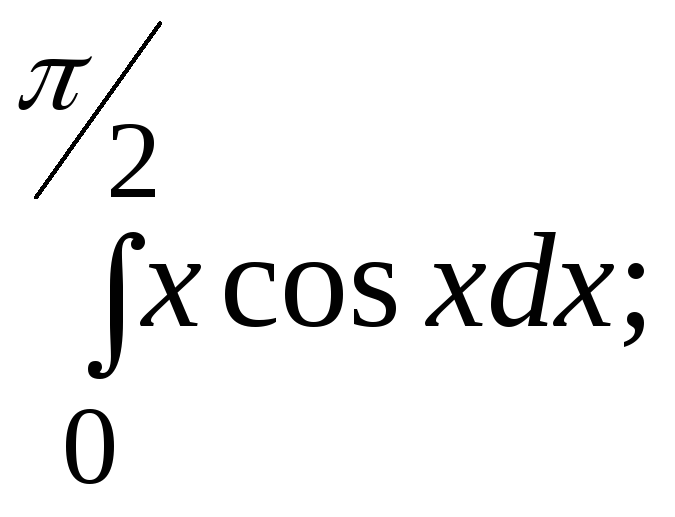

5.17. 5.18.

5.19. 5.20.

VI. Геометрические приложения определенного интеграла. Понятие несобственного интеграла

Вычисление площадей плоских фигур

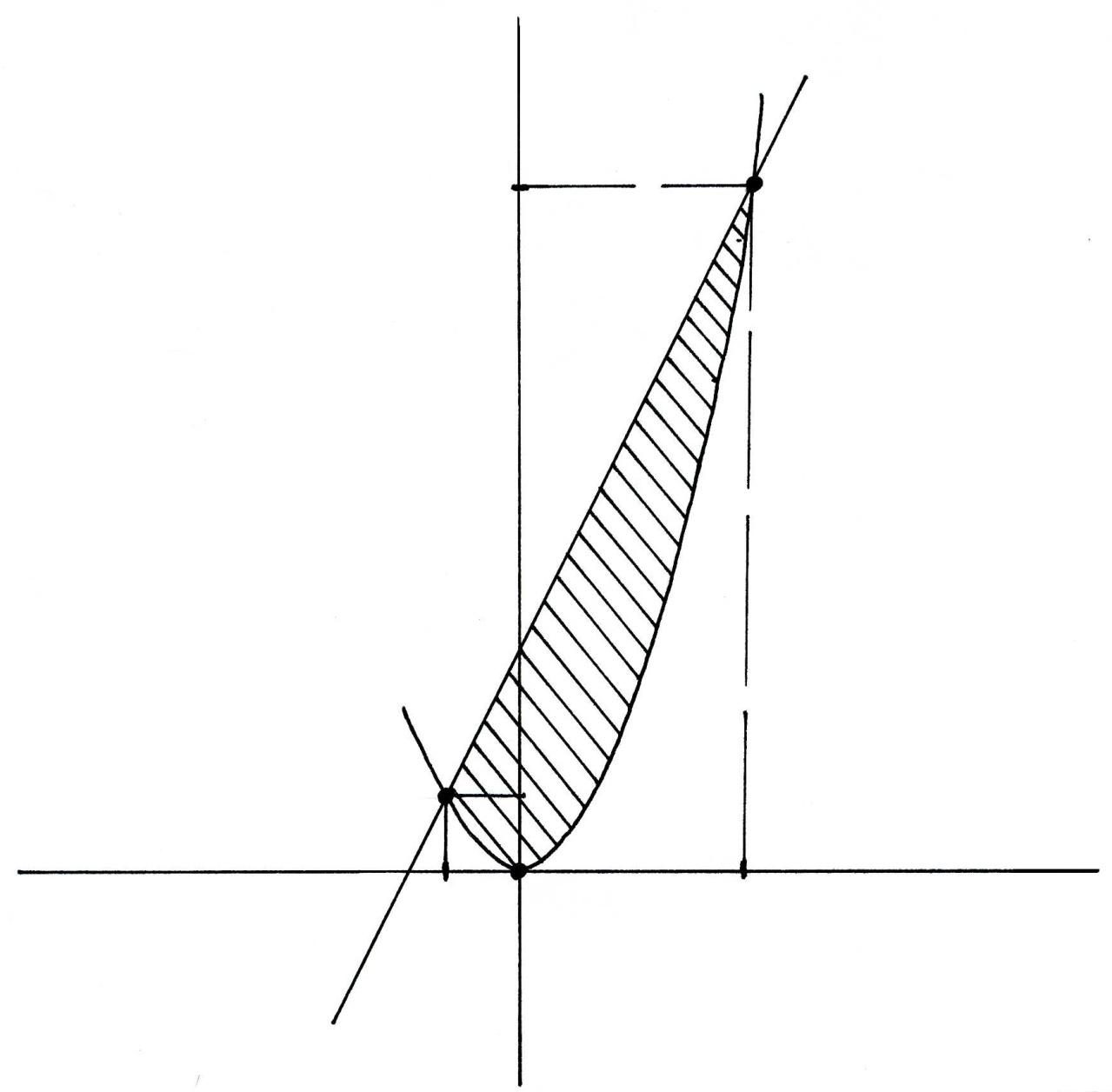
Пример 6.1. Вычислить площадь фигуры, ограниченной прямой и параболой.

Найдем точки пересечения прямой с параболой, решив совместно их уравнения:

Следовательно,, откуда находим:,.

x

y

Вычислить площадь, ограниченную следующими линиями:

6.1. Параболой прямойи осью

6.2. Параболой прямой

6.3. Параболой прямой

6.4. Параболами и

6.5. Кубическими параболами и

6.6. Параболой , осью

6.7. Полукубической параболой прямыми

6.8. Параболой прямой

6.9. Гиперболой прямой

6.10. Кубической параболой прямыми

6.11. Окружностью параболой

6.12. Параболой осью

6.13. Параболой , осью

6.14. Параболами

6.15. Параболой