
- •Введение
- •I. Вычисление пределов функции
- •Найти следующие пределы:
- •2.1. 2.2.
- •2.54. 2.55.
- •III. Исследование функций и построение графиков
- •Исследовать функции и построить их графики:
- •Формула замены переменной в определенном интеграле
- •Вычисление площади поверхности вращения
- •Вычисление объема тела вращения
- •Понятие несобственного интеграла
- •6.34. 6.35.
- •7.1. 7.2.
- •Линейные дифференциальные уравнения первого порядка
- •Уравнение Бернулли.
- •Уравнения высших порядков, допускающие понижение порядка
- •4. Вычислить площадь фигуры, ограниченной линиями:
- •5. Исследовать сходимость ряда:
- •6. Решить дифференциальное уравнение первого порядка:
- •2.51.2.52.
- •4.22. 4.23.4.24.
- •8.1. 8.2. 8.3. 8.4. 8.5. 8.6. 8.7. 8.8. 8.9. 8.10. 8.11.
Введение
В начале обучения студенты экономических и организационно – управленческих специальностей изучают курс высшей математики, который служит фундаментальной базой экономического и управленческого образования. Поэтому преподавание математических дисциплин для экономических и организационно – управленческих специальностей имеет следующие цели: ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических экономических и организационно – управленческих задач; привить умение самостоятельно изучать учебную литературу по математике и ее приложениям; развить логическое мышление и повысить общий уровень математической культуры; выработать навыки математического исследования прикладных вопросов и умение перевести экономическую и организационно – управленческую задачу на язык математики. Кроме того, изучение курса математики имеет важное значение и для последующей практической работы экономиста и управленца, а также является необходимым для успешного изучения естественнонаучных, общепрофессиональных и специальных дисциплин.
Настоящее учебно-методическое пособие предназначено для студентов очной и заочной форм обучения. Оно содержит более 400 задач по основным вопросам математического анализа: предел функции одной, производная функции, частные производные функции многих переменных, понятие градиента, исследование функций и построение графиков, неопределенный интеграл, определенный интеграл и геометрические приложения определенного интеграла, понятие несобственного интеграла, числовые ряды, дифференциальные уравнения. Подробно рассмотрены примеры решения некоторых типовых задач и представлены варианты контрольных заданий.
При подготовке настоящего пособия использованы примеры и задачи из следующих литературных источников:
- Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1964.
- Бохан К.А. и др. Курс математического анализа. Т.1.: Учебное пособие / Под ред. проф. Б.З. Вулиха. – М.: Просвещение, 1965.
- Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1975.
- Кундышева Е.С. Математика: Учебное пособие для экономистов. – 2-е изд. – М.: Издательско-торговая корпорация «Дашков Ко», 2006.
- Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред. В.И. Ермакова. – 2-е изд., испр. – М.: ИНФРА-М, 2008.
- Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др.]; под ред. проф. Н.Ш. Кремера. – 3-е изд. – М.: ЮНИТИ-ДАНА, 2007.
I. Вычисление пределов функции
1.Случай,
когда при
![]() или
или![]() функция
функция![]() представляет
отношение двух бесконечно малых величин
(случай ).
представляет
отношение двух бесконечно малых величин
(случай ).
Пример
1.1.
![]()
Решение.
Вначале убеждаемся, что предел функции
нельзя найти непосредственной
подстановкой, что при указанном изменении
аргумента она представляет отношение
двух бесконечно малых величин (случай
); затем делаем преобразования, чтобы
сократить дробь на множитель, стремящийся
к нулю. Разлагаем знаменатель на множители
и сокращаем дробь на
![]() .
.
![]() =
=![]()
![]()
Пример
1.2.
![]()
Решение. Разлагаем числитель и знаменатель дроби на множители, как квадратные трехчлены, по формуле:
![]()
где
![]() и
и![]() - корни трехчлена. Затем сокращаем дробь
на
- корни трехчлена. Затем сокращаем дробь
на![]() :
:
![]()
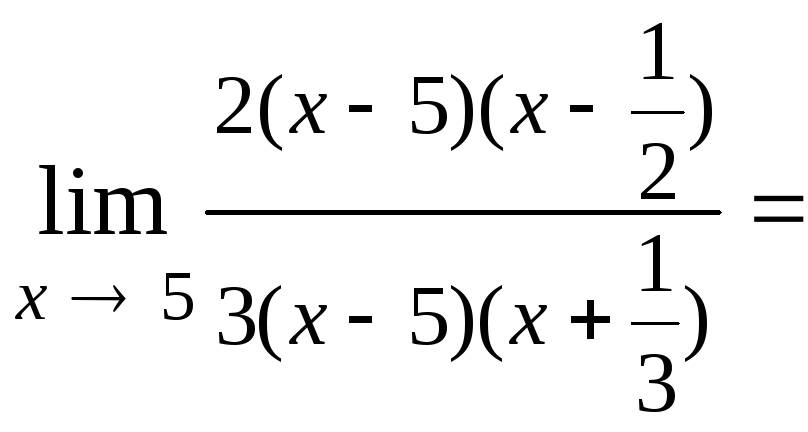
![]()
![]()
Вообще,
если ищется предел дроби, числитель и
знаменатель которой многочлены,
обращающиеся в нуль в предельной точке
![]() ,
то согласно теореме Безу оба многочлена
разделяются без остатка на
,
то согласно теореме Безу оба многочлена
разделяются без остатка на![]() ,
то есть такую дробь всегда можно сократить
на
,
то есть такую дробь всегда можно сократить
на![]() .
.
Таким
образом, сократим дробь, разделив на
![]() числитель и знаменатель в отдельности:
числитель и знаменатель в отдельности:
![]()
![]()
![]()
Пример
1.3.
![]()
Решение.
Уничтожаем иррациональность в числителе
путем умножения числителя и знаменателя
на
![]() ,
затем сокращаем дробь на
,
затем сокращаем дробь на![]() :
:
![]()
Пример
1.4.
![]()
Решение. Преобразуем функцию таким образом, чтобы использовать 1-й замечательный предел:
![]()
![]()
![]() (
(![]() радианная
мера угла).
радианная
мера угла).
Применяем тригонометрическую формулу:
![]()
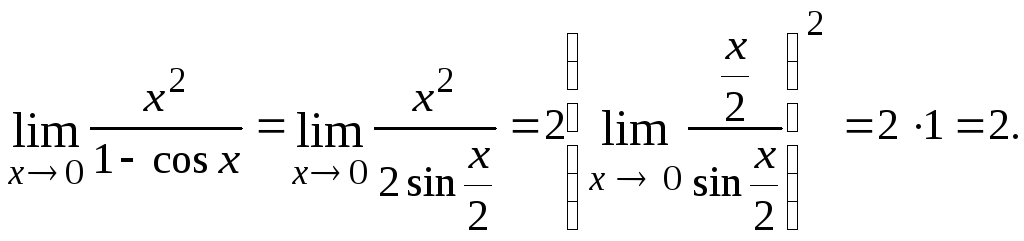
2.Случай,
когда при
![]() или
или![]() функция
функция![]() представляет
отношение двух бесконечно больших
величин (случай
представляет
отношение двух бесконечно больших
величин (случай![]() ).
).
Пример
2.1.
![]()
Решение.
Убедившись,
что имеет место случай
![]() ,
преобразуем функцию путем деления
числителя и знаменателя дроби на
,
преобразуем функцию путем деления
числителя и знаменателя дроби на![]() (наивысшая степень
(наивысшая степень![]() ):
):
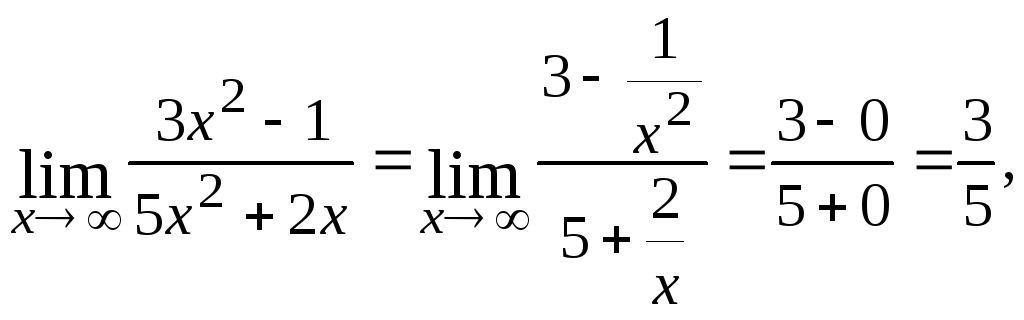
при
![]() величины
величины![]() и
и![]() являются бесконечно малыми.
являются бесконечно малыми.
Пример
2.2.
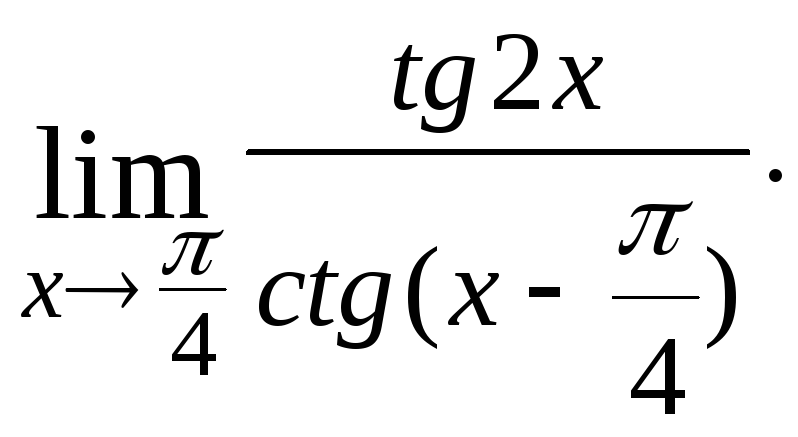
Решение. Тождественно преобразуем дробь так, чтобы затем сократить ее на множитель, стремящийся к нулю:
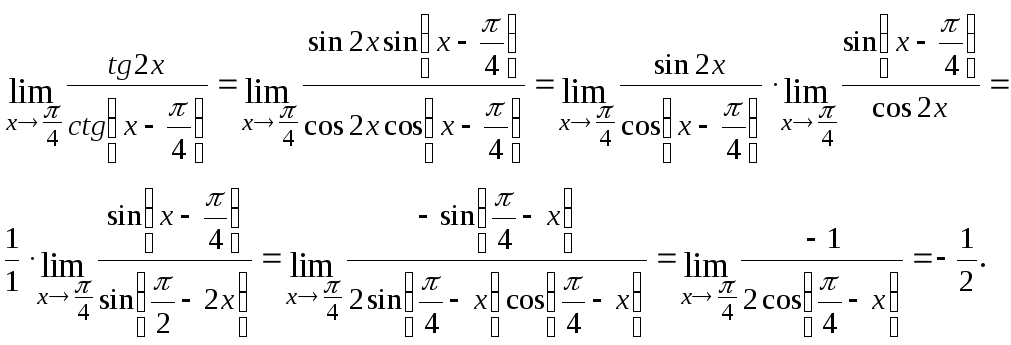
3.
Случай, когда при
![]() или
или![]() функция
функция![]() представляет
произведение бесконечно малой величины
на бесконечно большую (случай
представляет
произведение бесконечно малой величины
на бесконечно большую (случай![]() ).
).
Данный
случай нахождения предела функции
производится путем преобразования
функции к одному из двух рассмотренных
случаев, т.е. к случаю![]() или к случаю
или к случаю![]() .
.
Пример
3.1.
![]()
Решение.
Установив, что при указанном изменении
аргумента функция представляет
произведение бесконечно малой величины
на бесконечно большую (случай
![]() ),
преобразуем её к виду дроби, числитель
и знаменатель которой одновременно
стремятся к нулю или к бесконечности.
),
преобразуем её к виду дроби, числитель
и знаменатель которой одновременно
стремятся к нулю или к бесконечности.
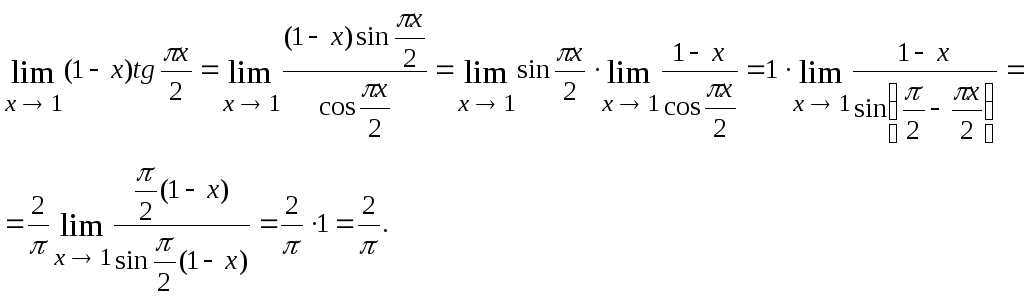
Пример
3.2.
![]()
Решение.
Положим
![]() тогда
тогда![]()
![]() когда
когда![]() и, следовательно,
и, следовательно,
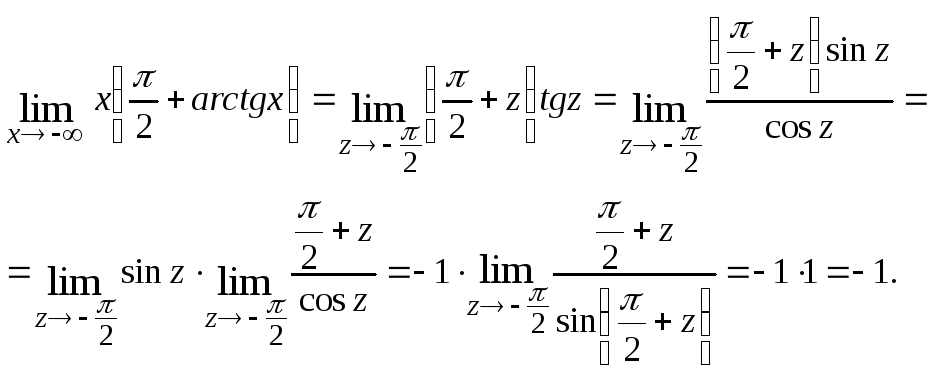
![]()
4.
Случай, когда при
![]() или
или![]() функция
функция![]() представляет разность двух положительных
бесконечно больших величин (случай
представляет разность двух положительных
бесконечно больших величин (случай![]() ).
).
Данный
случай нахождения предела функции можно
привести к случаю
![]() или
или![]() путем преобразования функции к виду
дроби.
путем преобразования функции к виду
дроби.
Пример
4.1.
![]()
Решение.
Делаем заключение, что при указанном
поведении аргумента функция представляет
разность двух положительных бесконечно
больших величин (случай
![]() ).
Преобразуем функцию к виду дроби,
числитель и знаменатель которой
одновременно стремятся к нулю или к
бесконечности.
).
Преобразуем функцию к виду дроби,
числитель и знаменатель которой
одновременно стремятся к нулю или к
бесконечности.
Производим
вычитание дробей и полученную в результате
дробь сокращаем на
![]() :
:
![]()
Пример 4.2.
![]()
![]()
5.
Случай, когда при
![]() или
или![]() функция
функция![]() представляет степень, основание которой
стремится к единице, а показатель – к
бесконечности (случай
представляет степень, основание которой
стремится к единице, а показатель – к
бесконечности (случай![]() ).
).
В данном случае для нахождения предела функции используется 2-й замечательный предел:
![]()
е = 2,7182818… - основание натурального логарифма ln.
Пример
5.1.
![]()
Решение.
При указанном изменении аргумента
функция представляет степень, основание
которой стремится к единице, а показатель
– к бесконечности (случай
![]() ).
Преобразуем функцию таким образом,
чтобы использовать 2-й замечательный
предел. Полагаем
).
Преобразуем функцию таким образом,
чтобы использовать 2-й замечательный
предел. Полагаем
![]() ,
получим, что при
,
получим, что при
![]()
![]() :
:
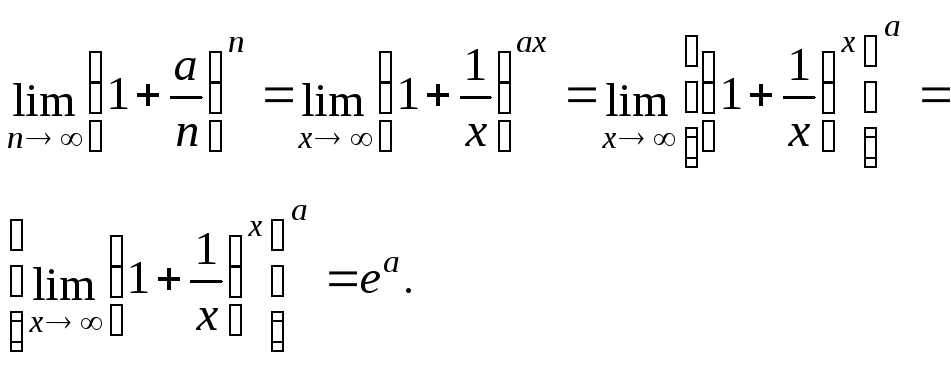
Пример
5.2.
![]()
Решение.
Полагаем
![]() получим,
что при
получим,
что при
![]()
![]() .
.
![]()
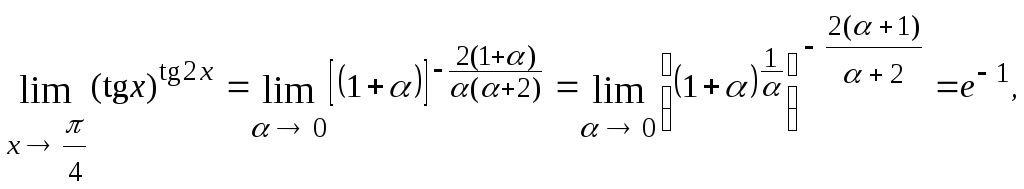
так
как
![]()
Вычисление предела функции по правилу Лопиталя.
Предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных, если он существует, или равен бесконечности.
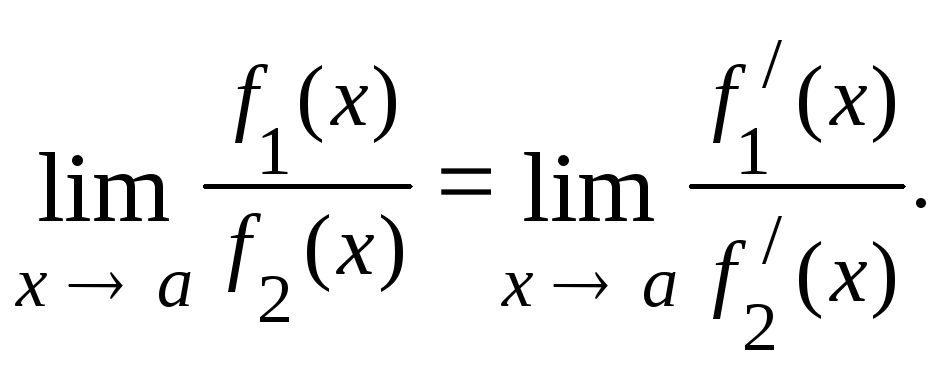
Правило Лопиталя можно применять последовательно несколько раз, если это полезно, до получения результата.
Пример
6.1.
![]()
Пример
6.2.
![]()
В примере 6.2 правило Лопиталя применено дважды.
