Логарифмическая функция Тригонометри́ческие фу́нкции

3 предел функции в точке. Определение гейне.

Преде́л фу́нкции  в заданной точке — такая величина, к которой стремится функцияпри стремлении её аргумента к данной точке.

Определение предела по Гейне. Число A называется пределом функции f(x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности такой, что сходящейся к числу a, соответствующая последовательность значений функции сходится к числу A.

4 предел функции в точке. Определение коши

Определение предела по Коши. Число A называется пределом функции f(x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0существует δ > 0 такое, что для всех x, удовлетворяющих условию |x–a| < δ, x≠a, выполняется неравенство |f(x) –A| < ε.

5 Предел функции в точке. Основные свойства

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

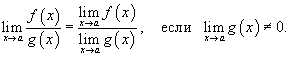
6 второй замечательный предел

Второй замечательный предел имеет вид:

или в другой записи

В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность .

7 Теорема о пределе монотонной функции.

Предел монотонной функции

Определение. Функция называется

- монотонно возрастающей, если из 

-строго монотонно возрастающей, если из 

- монотонно убывающей, если из 

-строго монотонно убывающей, если из .

Докажем одну из возможных здесь теорем.

Теорема. Если монотонно возрастает и ограниченна сверху при , то существует конечный предел слева.

Доказательство. Рассмотрим множество значений функции при. По условию теоремы, это множество ограниченно сверху, т.е. . По теореме о существовании супремума отсюда следует, что существует конечный .

Покажем, что . По свойствам супремума

1.

2. 

Обозначим . Возьмем любое x, для которого , но . Как видно из рисунка, из этого следует, что . Но тогда, в силу монотонности 

а) 

б) 

Поэтому имеем

Выбрасывая лишнее получим, что

или, что то же самое, . По определению предела функции это означает, что .

Аналогичные теоремы можно сформулировать и доказать также для монотонно убывающих функций, а так же для пределов слева.

8 Критерий Больцано-Коши

Критерий Коши:

Предел функции f(x) в точке a существует тогда и только тогда, если для каждого ε > 0 найдется такое δ = δ (ε) >0, что

|f(x' ) - f(x" )| < ε,

как только 0 < |x' - a| < δ и 0 < |x' - a| < δ, где x' и x" - любые точки из области определения функции f(x).

если непрерывная функция принимает два значение, то она принимает и любое значение между ними.

Пусть дана непрерывная функция на отрезке Пусть также и без ограничения общности предположим, что Тогда для любого существует такое, что 

9 эквивалентность бесконечно малых функций

Определение. Если то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.