1. теорема о существовании точных граней ограниченного множества

Теорема. ограниченное сверху непустое числовое множество имеет верхнюю грань, а всякое ограниченное снизу непустое числовое множество имеет нижнюю грань.

Доказательство. Пусть - ограниченное сверху непустое числовое множество. Обозначим через множество всех чисел, ограничивающих сверху множество . Множество ограничено сверху, поэтому множество не пусто. Каждый элемент ограничивает сверху множество , т.е. . Элементы и являются произвольными элементами соответственно множеств и , поэтому, в силу свойства непрерывности действительных чисел, и имеет место неравенство .

Выполнение неравенства означает, что число ограничивает сверху множество , а выполнение неравенства для всех , т.е. для всех чисел, ограничивающих сверху множество , означает, что число является наименьшим среди всех таких чисел, т.е. верхней гранью множества : .

-е верхней грани у ограниченного сверху непустого множества доказано.

Если теперь - непустое ограниченное снизу числовое множество, то отнесём к множеству все числа, ограничивающие снизу множество .

Аналогично рассмотренному случаю верхней грани, легко убеждаемся, что, в силу свойства неперрывности действительных чисел, и имеет место неравенство .

Это означает, что Теорема доказана.

2. леммы о бесконечно малых

Опр. 1: Переменная называется бесконечно малой, если её пределом является нуль.

 ЛЕММА №1: Для того чтобы переменная имела своим пределом постоянное число a, необходимо и достаточно выполнения равенства:

    – бесконечно малая величина.

 Результат следует из того, что разность есть расстояние от точкидо её предела, это расстояние стремится к нулю, т. к., и наоборот: если расстояние стремиться к нулю, то.

ЛЕММА №2: Алгебраическая сумма конечного числа бесконечно малых, есть величина бесконечно малая.

Доказательство:

Рассмотрим, например, сумму 3-х бесконечно малых.

Возьмем любое E > 0, т. к. ,то по определению существует номерn такой, что будет выполняться три неравенства:

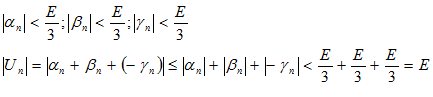(по лемме №2 о вещественных числах).

Существует номер n, такой, что при n > N выполняется неравенство:

    для , это и означает, что, Ч. Т. Д.

Лемма №3:Произведение ограниченной переменной на бесконечно малую есть величина басконечно малая Пусть

Требуется доказать, что:  

Доказательство:

Пусть 

Возьмем , т.к. – бесконечно малая, то существует номер N такой что при: , 

Тогда.

     , при , следовательно, выполняется неравенства:

    ,    

Это и означает, что: – бесконечно малая.

3. Арифметические свойства пределов

Предел суммы двух функций равен сумме пределов этих функций:

Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

Предел произведения функции на постоянную величину

Постоянный коэффициент можно выносить за знак предела:

Предел произведения

Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):

Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

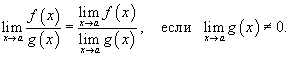
Предел логарифмической функции

где основание a > 0. 

4 лемма о вложенных отрезках

Для всякой системы вложенных отрезков

существует хотя бы одна точка , принадлежащая всем отрезкам данной системы.

Если, кроме того, длина отрезков системы стремится к нулю:

то — единственная общая точка всех отрезков данной системы.

1) Существование общей точки. Множество левых концов отрезков лежит на числовой прямой левее множества правых концов отрезков, поскольку

В силу аксиомы непрерывности, существует точка , разделяющая эти два множества, то есть

в частности

Последнее неравенство означает, что — общая точка всех отрезков данной системы.

2) Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки и, принадлежащие всем отрезкам системы:

Тогда для всех номеров выполняются неравенства:

В силу условия стремления к нулю длин отрезков для любого для всех номеров, начиная с некоторого будет выполняться неравенство

Взяв в этом неравенстве , получим

Противоречие. Лемма доказана полностью.

5 Лемма Больцоно-Вейерштрасса

    Теорема. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

     Доказательство. Так как последовательность ограничена, то она имеет хотя бы одну предельную точку x. В таком случае из этой последовательности можно выделить подпоследовательность, сходящуюся к точке x.

     Замечание 1. Из любой ограниченной последовательности можно выделить монотонную подпоследовательность.

     В самом деле, в силу теоремы Больцано-Вейерштрасса из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность, а из этой подпоследовательности можно выделить монотонную подпоследовательность.

     Замечание 2. Пусть {x_n} - ограниченная последовательность, элементы которой находятся в сегменте [a, b]. Тогда предел с любой сходящейся подпоследовательности также находится на сегменте [a, b].

6 критерий коши

Теорема ( Критерий Коши ). Для того, чтобы последовательность сходилась, необходимо и достаточно чтобы она была фундаментальной.

Доказательство.

Необходимость. Пусть сходится. 

 

Достаточность. Пусть - фундаментальная последовательность. Докажем, что она ограничена и .

Так как последовательность фундаментальна, то , в -окресности которой существуют все элементы .

Положим, .

В отрезке [A, -A] содержатся все элементы последовательности, т.е. - ограниченна.

В следствие теоремы Больцано-Вейерштрасса () < ().

 в силу произвольности 

7 теорема о пределе монотонной последовательности

  Определение.

Последовательность {x_n} называется монотонно возрастающей, если для любого n    x_n+1  x_n.

Теорема о существовании предела монотонной последовательности.

1. Если последовательность {x_n} монотонно возрастает (убывает) и ограничена сверху (снизу), то у нее  существует конечный предел, равный sup{x_n} ( inf{x_n} ).

2 Если последовательность {x_n} монотонно возрастает (убывает), но сверху (снизу) не ограничена, то у нее  существует предел, равный + ( - ).

Теорема:

1. Если последовательность монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу;

2. Если последовательность монотонно возрастает, но неограниченна сверху, то.

Доказательство.