2.3. Основные понятия проверки статистических гипотез

Нахождение точечных и интервальных оценок является только предварительной стадией исследования. Конечная цель исследования может заключаться в сравнительной оценке различных технологических процессов по их производительности, точности или экономичности. Относительно эконометрических моделей это может быть более высокая надёжность или точность полученных моделей [1, 3, 4].

Большинство эконометрических моделей требуют многократного улучшения и уточнения. Для этого необходимо проведение соответствующих расчетов, связанных с установлением выполнимости или невыполнимости тех или иных предпосылок, анализом качества найденных оценок, достоверностью полученных выводов. Обычно эти расчеты проводятся по схеме статистической проверки гипотез. Поэтому знание основных принципов проверки гипотез является обязательным для эконометриста.

Во многих случаях необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид (назовем его А), выдвигают гипотезу: генеральная совокупность случайной величины X распределена по закону распределения А. Например, можно выдвинуть предположение, что доход населения, ежедневное количество покупателей в магазине, размер выпускаемых деталей имеют нормальный закон распределения.

Статистической гипотезой называется гипотеза о предполагаемом виде закона неизвестного распределения или о параметрах известных распределений.

Например, статистическими являются гипотезы о том, что генеральная совокупность распределена по закону Пуассона или о том, математические ожидания двух нормальных совокупностей равны между собой.

Статистическая гипотеза называется параметрической, если в ней сформулированы предположения относительно значений параметров функции распределения известного вида.

Статистическая гипотеза называется непараметрической, если в ней сформулированы предположения относительно вида функции распределения.

Метод использования выборки для проверки истинности (ложности) статистической гипотезы называется статистическим доказательством истинности выдвинутой гипотезы.

Наряду с выдвинутой гипотезой рассматривают одну или несколько альтернативных гипотез. Если выдвинутая гипотеза отвергается, то ее место занимает альтернативная гипотеза. Поэтому статистические гипотезы подразделяются на нулевые и альтернативные.

Нулевой (или основной) гипотезой H₀ называется гипотеза, которая утверждает, что различие между сравниваемыми величинами отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями выборки.

Альтернативной (или конкурирующей) гипотезой H₁ называется гипотеза, которая противоречит основной.

Статистическая гипотеза называется простой, если она содержит только одно предположение, т.е. если ей соответствует одно распределение или одна точка пространства параметров. Гипотеза называется сложной, если она сводится к выбору какого-либо распределения из целого множества или выбору точки из интервала конечного или бесконечного.

Очевидно, что на основе статистических данных очень трудно, а иногда и невозможно делать безошибочные выводы. Ошибки при проверке гипотез могут быть двух родов.

Ошибка первого рода состоит в том, что отвергается основная гипотеза, когда на самом деле она верна. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Возможные результаты статистических выводов представлены следующей таблицей:

Результаты проверки гипотезы	Возможные состояния гипотезы
	верна H0	верна H1
Гипотеза H0 отклоняется	Ошибка первого рода	Правильный вывод
Гипотеза Н0 не отклоняется	Правильный вывод	Ошибка второго рода

Для проверки нулевой гипотезы используют специально подобранную случайную величину – выборочную статистику K, точное или приближенное распределение которой известны.

Случайная величина K, которая служит для проверки нулевой гипотезы, называется статистическим критерием.

Пусть определен статистический критерий K и пусть плотность вероятностей выборочной статистики K при условии истинности нулевой гипотезы H₀ равна f(KH₀), математическое ожидание K равно K₀. Тогда вероятность попадания критерия K в интервал (K_/2; K_1-/2) можно найти по формуле:

. (2.11)

Зададим эту вероятность равной 1- и вычислим критические точки (квантили) K-распределения K_/2 и K_1-/2 из условия:

; (2.12)

, (2.13)

где значение  задается достаточно малым (0,05 или 0,01), чтобы попадание случайной величины K за пределы интервала (K_/2, K_1-/2) можно было бы считать маловероятным событием.

Следовательно,

,

а значит

.

Рис. 2.5. Двусторонняя критическая область

Область (K_/2, K_1-/2) называется областью допустимых значений. Области (-;K_/2) и (K_1-/2, +) называются критическими областями критерия, т.е. критической областью называется совокупность значений критерия K, при попадании в которую наблюдаемого значения К нулевую гипотезу отвергают.

Точки, отделяющие критические области от области принятия гипотезы, называются критическими точками.

Рис. 2.6. Правосторонняя критическая область

Критическая область называется двусторонней, если она располагается слева и справа от математического ожидания, правосторонней, если Р(K> K_1-) = , (рис. 2.6),

и левосторонней, если Р(K<K_) = , (рис. 2.7).

Рис. 2.7. Левосторонняя критическая область

Итак, основной принцип проверки статистической гипотезы можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области допустимых значений – гипотезу принимают.

Вероятность  совершить ошибку первого рода называется уровнем значимости или размером критерия.

Вероятность 1- не совершить ошибку второго рода называется мощностью критерия K.

Дадим геометрическую интерпретацию вероятностей ошибок первого и второго рода и мощности критерия, имеющего левостороннюю критическую область: передвигая квантиль K_ влево – уменьшая ошибку первого рода, – увеличиваем ошибку второго рода (рис. 2.8). Единственным способом одновременного уменьшения вероятностей ошибок первого и второго рода является увеличение числа выборок.

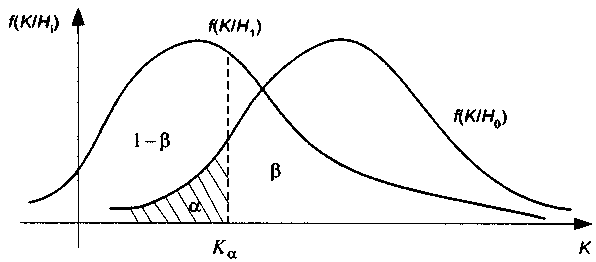
Рис. 2.8. Ошибки первого и второго рода

В общем случае задача проверки истинности нулевой гипотезы рассматривается так: любую выборку объема n можно изобразить как точку в n-мерном пространстве Rⁿ, которое называется выборочным. Если наблюдается несколько выборок из генеральной совокупности N(a, ²), то точки в n-мерном пространстве будут концентрироваться около точки с координатами (a, a, ..., a). Например, для n = 2 (рис. 2.9) – число точек равно числу выборок, а «облако» точек около точки (0, 0) соответствует выборкам из нормальной совокупности N(0, ²), и «облако» около точки (a, a) – выборкам из совокупности N(а, ²). По расположению точек можно узнать, какая гипотеза верна.

Рис. 2.9. Расположение выборок

Значит, n-мерное пространство можно разделить на две области: основной гипотезе соответствует одна область, а альтернативной – другая. Если выборочная точка принадлежит области, соответствующей конкурирующей гипотезе, то основная гипотеза отклоняется.

Область S, при попадании в которую выборочной точки отвергается основная гипотеза, называется критической.

Вероятность P(SH₀) отвергнуть верную основную гипотезу есть вероятность ошибки первого рода, она называется уровнем значимости или размером критерия. Уровень значимости задается заранее и достаточно мал – 0,05; 0,01 и т.д.

Если уровень значимости  достаточно мал, то высока надежность критерия, т.е. вероятность принять основную гипотезу, когда она верна.

Если – множество, при попадании в которое выборочной точки отвергается конкурирующая гипотеза, т.е. принимается верная основная гипотеза, то надежность критерия равна:

.

Зафиксируем уровень значимости  и будем рассматривать только критические множества S с этим фиксированным уровнем. Вероятность ошибки второго рода – вероятность отвергнуть верную конкурирующую гипотезу (а значит, принять нулевую гипотезу, когда она неверна).

Основным (хорошим) свойством статистического критерия должна быть минимальность ошибки второго рода при фиксированной ошибке первого рода. Так как , то при_min, вероятность отвергнуть основную гипотезу, если верна конкурирующая, будет максимальной.

Вероятность попадания точки (выборки) в критическое множество, когда верна конкурирующая гипотеза, называется мощностью критерия, т.е. если

,

то S₀ – наилучшая критическая область (НКО).