Reshebnik_Demidovicha_narodny

http://www.truba.nnov.ru/solver

№ 1 Задание: Применяя метод математической индукции, доказать, что 1+2+...+n = n(n+1)/2. Решение: Проверяем формулу для n=1: 1 = 1 · 2 / 2. Формула верна. Применяем метод мат. индукции. Пусть формула верна для n членов. Докажем, что она верна и для n+1 члена. Для n+1 получим: Как мы видим, формула верна и для n+1, значит формула верна для любых n.

№ 2 Задание: Применяя метод математической индукции, доказать, что: Решение: Проверяем формулу для n=1: 1 = 1 · 2 · 3 / 6. Формула верна. Применяем метод мат. индукции. Пусть формула верна для n членов. Докажем, что она верна и для n+1 члена. Для n+1 получим: Как мы видим, формула верна и для n+1, значит формула верна для любых n.

№ 3 Задание: Применяя метод математической индукции, доказать, что 1³+2³+...+n³=(1+2+...+n)². Решение: Заметим, что (1+2+...+n)² = = 1²+2²+...+n²+2 · 1 · 2 + 2 · 1 · 3 + ... + 2 · 1 · n + 2 · 2 · 3 + ... + 2 · 2 · n + ... + 2 · (n - 1) · n Проверяем формулу для n=1: 1 = 1. Формула верна. Применяем метод мат. индукции. Пусть формула верна для n членов. Докажем, что она верна и для n+1 члена. Для n+1 получим: 1³+2³+...+n³+(n+1)³=(1+2+...+n)² + (n+1)³ = (1+2+...+n)² + (n+1)² + n · (n+1)² = = (1+2+...+n)² + (n+1)² + ^{n · (n+1)}/₂ · 2(n+1) = (1+2+...+n)² + (n+1)² + 2(n+1) · (1 + 2 + ... + n) = = (1+2+...+n+(n+1))² Как мы видим, формула верна и для n+1, значит формула верна для любых n.

№ 4 Задание: Применяя метод математической индукции, доказать, что 1+2+2²...+2^n-1=2ⁿ-1. Решение: Проверяем формулу для n=1: 2⁰ = 2¹-1. Формула верна. Применяем метод мат. индукции. Пусть формула верна для n членов. Докажем, что она верна и для n+1 члена. Для n+1 получим: 1+2+2²...+2^n-1+2ⁿ=2ⁿ - 1 + 2ⁿ = 2 · 2ⁿ - 1 = 2ⁿ⁺¹ - 1. Как мы видим, формула верна и для n+1, значит формула верна для любых n.

№ 5 Задание: Пусть a^[n]=a(a-h)(a-2h)...(a-(n-1)h) и a^[0]=1. Доказать, что где C_n^m - число сочетаний из n элементов по m. Вывести отсюда формулу бинома Ньютона. Решение: Укажем несколько свойств числа сочетаний C_n^m: Проверяем формулу для n=0: 1 = 1. Формула верна. Применяем метод мат. индукции. Пусть формула верна для n членов. Докажем, что она верна и для n+1 члена. Для n+1 получим: Как мы видим, формула верна и для n+1, значит формула верна для любых n. Очевидно, что если h=0, то a^[n] = aⁿ, а значит справедлива формула бинома Ньютона:

№ 6 Задание: Доказать неравенство Бернулли: (1+x₁)(1+x₂)...(1+x_n) > 1 + x₁ + x₂ + ... + x_n, где x_i - числа одного и того же знака, > -1. Решение: Проверяем неравенство для n=1: 1 + x₁ > 1 + x₁. Неравенство верно. Применяем метод мат. индукции. Пусть неравенство верно для n членов, т.е. верно неравенство (1+x₁)(1+x₂)...(1+x_n) > 1 + x₁ + x₂ + ... + x_n. Умножим его на неотрицательное число 1 + x_n+1 (оно неотрицательно, т.к. x_i > -1). Получим: (1+x₁)(1+x₂)...(1+x_n)(1+x_n+1) > (1 + x₁ + x₂ + ... + x_n) + (x_n+1 + x_n+1x₁ + x_n+1x₂ + ... + x_n+1x_n). Т. к. x_i одного знака, произведения в правой части положительны, и если их отбросить, неравенство только усилится. Получаем: (1+x₁)(1+x₂)...(1+x_n)(1+x_n+1) > 1 + x₁ + x₂ + ... + x_n + x_n+1. Как мы видим, неравенство верно и для n+1 членов, а значит верно для любых n.

№ 7 Задание: Доказать, что если x>-1, то справедливо неравенство (1+x)ⁿ > 1+nx. (n>1), причём знак равенства имеет место только при x=0. Решение: Будем считать, что x отлично от 0, а неравенство, которое нужно доказать - строгое. Докажем неравенство индукцией по n. 1. Проверяем для n=2: (1+x)² = 1 + 2x + x² > 1 + 2x, т.к. x != 0. 2. Пусть неравенство верно для n. Покажем, что оно верно и для n+1. Для этого умножим исходное неравенство на положительное число (x+1): Левая часть примет вид: (1+x)ⁿ(1+x) = (1+x)ⁿ⁺¹, а правая - (1 + nx)(1 + x) = 1 + (n+1)x + nx², т.е. (1+x)ⁿ⁺¹ > 1 + (n+1)x + nx² > 1 + (n+1)x (т.к. nx² > 0). Таким образом, неравенство справедливо для n+1, а значит (по индукции) и для любых n. Заметим ещё раз, что мы доказали строгое неравенство для случая x != 0. Очевидно, что при х=0 оно обращается в равенство 1=1, таким образом, исходное нестрогое неравенство верно, и обращается в равенство только при х=0, что и требовалось доказать.

№ 8 Задание: Доказать неравенство для n>1: Указание: использовать неравенство Решение: Проверяем неравенство для n=1: 2 < 2.25. Неравенство верно. Применяем метод мат. индукции. Пусть неравенство верно для n членов, т.е. верно неравенство Умножим его на положительное число n + 1. Получим: Теперь умножим получившееся неравенство на неравенство из Указания. Получим: Как мы видим, неравенство верно и для n+1 членов, а значит верно для любых n.

№ 9 Задание: Доказать неравенство: 2! · 4! · ... · (2n)! > [(n+1)!]ⁿ при n>1 Решение: Докажем методом мат. индукции. Для n=2: 2! · 4! = 48 > 6² = 36. Пусть неравенство верно для n. Докажем, что оно верно для n+1. Для этого рассмотрим неравенство (1): (2n+2)! > (n+2)ⁿ · (n+2)!. Докажем, что (1) верно для n>1: (2n+2)! = (n+2)! · (n+3) · (n+4) · ... · (2n+2). Сократим обе части неравенства на (n+2)! > 0. Получим: (n+3) · (n+4) · ... · (2n+2) > (n+2)ⁿ. Это неравенство очевидно верно, т.к. с обеих сторон n сомножителей, но каждый сомножитель справа меньше любого сомножителя слева. Теперь домножим исходное неравенство для n (верное по предположению индукции) на неравенство (1). Знак неравенства при этом не изменится. Получим: 2! · 4! · ... · (2n)! · (2n+2)! > [(n+1)!]ⁿ · (n+2)ⁿ · (n+2)! = [(n+2)!]ⁿ · (n+2)! = [(n+2)!]ⁿ⁺¹. Получаем, что исходное неравенство верно и для n+1. Значит по индукции оно верно для любых n>1.

№ 10 Задание: Доказать неравенство методом математической индукции: Решение: 1. Проверяем неравенство при n=1: Неравенство выполняется. 2. Пусть неравенство верно для n. Докажем, что оно верно и для n+1. Для этого рассмотрим вспомогательное неравенство (1): Докажем, что неравенство (1) верно для n=1,2,3,.. . Для этого умножим обе его части на положительное число , знак неравенства при этом не изменится. Получим: Поскольку квадратный корень - строго монотонно возрастающая функция, мы можем избавиться от него, не повлияв на справедливость неравенства: Перенесём оба частных в левую часть и приведем их к общему знаменателю: Поскольку знаменатель - положительное число, умножим на него обе части неравенства, не повлияв на его справедливость, и раскроем скобки: 4n² + 8n + 3 - 4n² - 8n - 4 = -1 < 0. Неравенство обратилось в тождественное неравенство, а значит неравенство (1) верно. Умножим на него исходное неравенство (это можно сделать, т.к. все части обоих неравенств положительны): Т.е. исходное неравенство верно и для n+1, а значит, по индукции, и для любых n.

№ 22 Задание: Решить неравенство |x+1| < 0.01 Решение: -0.01 < x+1 < 0.01 -1.01 < x < -0.99

№ 23 Задание: Решить неравенство |x-2|>=10. Решение: 1) x-2>=10 x>=12 2) x-2<=-10 x<=-8 Ответ: x>=12 x<=-8

№ 30 Задание: Доказать тождество: Решение: Рассмотрим два случая. При x>0: При x<0: Тождество доказано.

№ 50 Задание: Предполагая, что n пробегает ряд натуральных чисел, определить значение выражения. (|a| < 1, |b| < 1) Решение: В числителе и знаменателе, очевидно, находятся суммы геометрических прогрессий. Раскроем этот предел, применив формулу для бесконечной суммы геометрической прогрессии.

№ 57 Задание: Предполагая, что n пробегает натуральный ряд чисел, определить значение следующего выражения: Решение: Преобразуем исходное выражение и воспользуемся формулой суммы бесконечной убывающей геометрической прогрессии:

№ 81 Задание: Пользуясь теоремой о существовании предела монотонной и ограниченной последовательности, доказать сходимость последовательности: Решение: 1. Заметим, что 2. Докажем, что x_n < 2. Для этого воспользуемся методом мат. индукции. Очевидно, что x₁ < 2. Пусть x_n < 2. Покажем, что тогда x_n+1 < 2: 3. Докажем теперь, что последовательность монотонно возрастает. Для этого рассмотрим отношение: Отношение последующего члена к предыдущему > 1, значит последовательность монотонно возрастает. Итак, последовательность монотонно возрастает и ограничена сверху, значит она имеет предел.

№ 86 Задание: Говорят, что последовательность x_n (n=1,2,...) имеет ограниченное изменение, если существует число С такое, что |x₂ - x₁| + |x₃ - x₂| + ... + |x_n - x_n-1| < C (n = 2,3,...). Доказать, что последовательность с ограниченным изменением сходится. Построить пример сходящейся последовательности, не имеющей ограниченного изменения. Решение: Пусть y_n = |x₂ - x₁| + |x₃ - x₂| + ... + |x_n - x_n-1| (n=2,3,...) и y₁ = 0. Т. к. последовательность y_n не убывает (сумма неотрицательных чисел) и ограничена сверху (числом С), она имеет предел, а значит для неё выполняется критерий Коши: Запишем теперь критерий Коши для исходной последовательности и докажем, что он также выполняется (далее, не уменьшая общности, будем считать, что k < n, a < b): Заметим теперь, что |y_n - y_k| = |x_k+1 - x_k| + |x_k+2 - x_k+1| + ... + |x_n - x_n-1|, |x_a - x_b| = |x_a - x_a+1+x_a+1 - x_a+2+x_a+2 - ... - x_b-1+x_b-1 - x_b| < < |x_a - x_a+1| + |x_a+1 - x_a+2| + ... + |x_b-1 - x_b| = |y_b - y_a|. Значит, критерий Коши выполняется и для x_n: Таким образом, исходная последовательность сходится. Приведем теперь пример сходящейся последовательности, не имеющей ограниченного изменения. Такой последовательностью будет, например, x_n = sgn cos (pi · x) · ¹/_n. (напомните мне это доказать)

№ 93 Задание: Доказать, что сходящаяся числовая последовательность ограничена. Решение: Запишем определение сходящейся последовательности. Если последовательность x_n сходится к А, то Пусть е = 1, а соответствующее ему N = N₀. Тогда исходную последовательность можно разбить на два множества: конечное множество С, состоящее из первых N₀ членов последовательности, и счётное множество Е из всех остальных членов последовательности. Очевидно, что все члены множества Е лежат в интервале (А - 1, А + 1), а среди чисел из множества С можно выбрать минимальное (Cmin) и максимальное (Cmax) (т.к. множество С конечно). Если теперь положить Xmin = min(A - 1, Cmin), Xmax = max(A + 1, Cmax), то все члены последовательности будут лежать на отрезке [Xmin, Xmax]. Таким образом, исходная последовательность ограничена.

№ 210 Задание: Пусть f_n(x) = f(f(f(...f(x)))) (n раз). Найти f_n(x), если Решение: Найдём сначала f(f(x)): Логично предположить, что Докажем это методом математической индукции. Мы знаем, что формула верна для n=2. Пусть она верна для n. Покажем, что тогда она верна и для n+1: Формула верна. Итак,

№ 213.1 Задание: Найти f(x) если f(^x/_x+1) = x². Решение: Преобразуем исходное выражение: Отсюда видно, что

№ 411 Задание: Найти значение выражений: a) б) Решение: a) б)

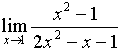
№ 412 Задание: Найти предел: Решение:

№ 439 Задание: Найти предел: Решение:

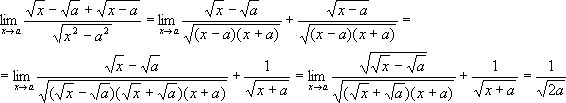
№ 475 Задание: Вычислить предел: Решение:

№ 477 Задание: Вычислить предел: 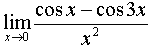Решение:

№ 479 Задание: Вычислить предел: Решение:

№ 506 Задание: Вычислить предел: а) б) в) Решение: а) б) в)

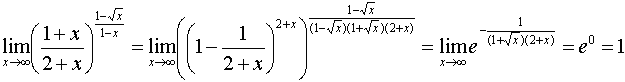
№ 542 Задание: Вычислить предел: Решение:

№ 545.2 Задание: Вычислить предел: Решение:

№ 557 Задание: Вычислить предел: Решение:

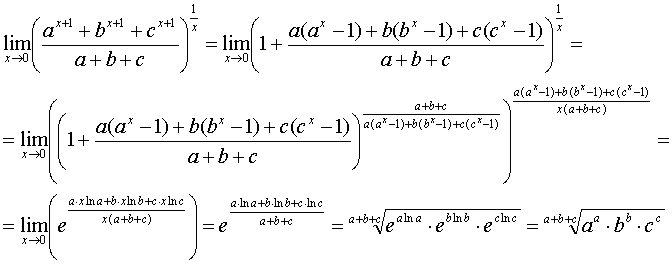
№ 561 Задание: Вычислить предел: а) б) Решение: а) б)

№ 571 Задание: Вычислить предел: Решение:

№ 582 Задание: Вычислить предел: Решение:

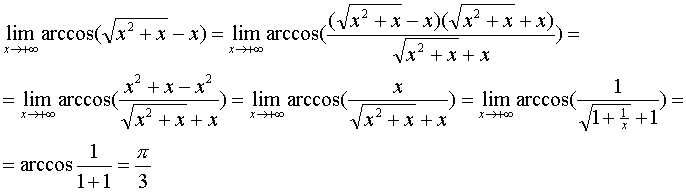
№ 886 Задание: Вычислить y', если y=lg³x². Решение: y' = 3 (lg²x²) · (lg x²)' = 3 (lg²x²) · (^{lg e}/_x² · 2x) = ⁶/_x lg e · lg²x²

№ 887 Задание: Вычислить производную функции: Решение:

№ 888 Задание: Вычислить производную функции: y = ln ln² ln³ x Решение:

№ 889 Задание: Вычислить производную функции: Решение:

№ 895 Задание: Вычислить производную функции: Решение:

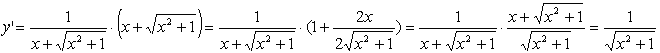
№ 896 Задание: Вычислить производную функции: Решение: См. также №895

№ 904 Задание: Вычислить производную функции: Решение:

№ 907 Задание: Вычислить производную функции: Решение:

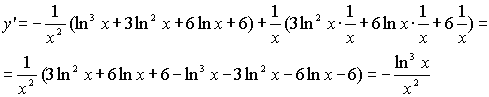
№ 961 Задание: Вычислить производную функции: Решение:

№ 986 Задание: Вычислить производные, если f(u) - дифференцируемая функция. а) y = f(x²) б) y = f(sin²x)+f(cos²x) в) y = f(e^x) · e^f(x) г) y = f(f(f(x))) Решение: а) y' = f'(x²) · (x²)' = f'(x²) · 2x б) y' = f'(sin²x) · (sin²x)' + f'(cos²x) · (cos²x)' = = f'(sin²x) · 2 · sin x · cos x - f'(cos²x) · 2 · cos x · sin x = sin 2x · (f'(sin²x) - f'(cos²x)) в) y' = f'(e^x) · e^x · e^f(x) + f(e^x) · e^f(x) · f'(x) = e^f(x) · [f'(e^x) · e^x + f'(x) · f(e^x)] г) y' = f'(f(f(x)) · (f(f(x)))' = f'(f(f(x))) · f'(f(x)) · f'(x)

№ 986.1 Задание: Найти f'(0) если f(x) = x (x-1)(x-2)...(x-1000). Решение: Очевидно, что если раскрыть все скобки, f(x) будет представлять собой полином степени 1001, т.е. f(x) = a₀x¹⁰⁰¹ + a₁x¹⁰⁰⁰ + ... + a₁₀₀₀x, где a_i - некие коэффициенты. Возьмём производную: f'(x) = 1001 · a₀x¹⁰⁰⁰ + ... + 2 · a₉₉₉x + a₁₀₀₀. При x=0 все члены, кроме последнего, обратятся в 0. Таким образом, f'(0) = a₁₀₀₀. Из исходной записи функции видно, что a₁₀₀₀ = -1 · -2 · -3 · ... · -1000 = 1000!. Таким образом, f'(0) = 1000! .

№ 1252 Задание: Объяснить, почему не верна формула Коши для функций f(x) = x² и g(x) = x³ на сегменте [-1,1]. Решение: Для того, чтобы формула Коши была справедлива, должны выполняться четыре условия: 1. f(x) и g(x) определены и непрерывны на сегменте [a,b] 2. f(x) и g(x) имеют конечные производные на интервале (a,b) 3. f'(x) и g'(x) не обращаются одновременно в 0 на интервале (a,b) 4. g(a) не равно g(b) Как мы можем видеть, условие 3 нарушается в точке x = 0 - обе производные обращаются в 0. Поэтому формула Коши не верна для данного случая.

№ 1674 Задание: Путём надлежащего преобразования подынтегрального выражения вычислить интеграл: Решение:

№ 2552 Задание: Доказать непосредственно сходимость ряда и найти его сумму: Решение:

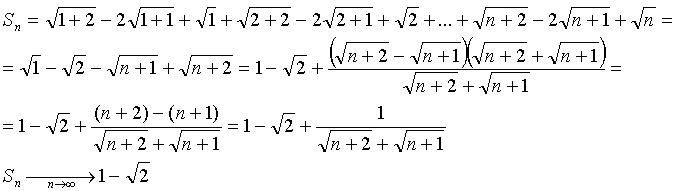
№ 2757 Задание: Исследовать последовательность на равномерную сходимость в указанном промежутке: f_n(x)=e^n(x-1); 0 < x < 1 Решение: Запишем определение равномерной сходимости по Гейне: и его отрицание: Далее рассмотрим исходную последовательность: т. е. f(x) = 0. r_n(x) = |f_n(x) - f(x)| = e^n(x-1) При x_n = 1 - ¹/_n, r_n(x) = e^-1, а значит Т. е. последовательность не обладает равномерной сходимостью на указанном интервале.

№ 3843 Задание: С помощью эйлеровых интегралов вычислить интеграл: Решение:

№ 3844 Задание: С помощью эйлеровых интегралов вычислить интеграл: Решение: См. №3843

№ 4115 Задание: Вычислить объём тела, ограниченного поверхностью, заданной формулой: Решение: Перейдём к обобщённым сферическим координатам: Т. к. данное тело очевидно симметрично относительно всех координатных плоскостей, вычислим 1/8 его объёма и умножим на 8: Сделаем замену: Получаем:

№ 4231 Задание: Найти длину дуги пространственной кривой (параметры положительны): x = 3t, y = 3t², z = 2t³ от O(0,0,0) до A(3,3,2). Решение: Очевидно, что в (·)О t=0, а в (·)А t=1.