2. Метод главных компонент

   1. Основные понятия и определения

Задача снижения размерности набора данных состоит в описании точек данных с помощью величин количеством меньшим по сравнению с размерностью пространства. Данные величины должны быть функциями исходных координат, т. е. :

ŋ_k=F_k(ξ₁, ξ₂,…, ξ_m), k = 1… m', m' < m.

Функции F_k задают отображение F из исходного пространства R^m в пространство R^m'.

В методе главных компонент F – некоторое линейное ортогональное нормированное отображение, т. е. :

F_k(ξ₁, ξ₂,…, ξ_m) = c_1k(ξ₁-µ₁)+…+c_mk(ξ_m-µ_m), где µ_j=-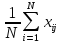

средние по набору данных значения признаков, а на коэффициенты c_ij накладываются условия:

, , i,j=1…m,i≠j.

Вид критерия J:

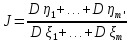, где D вычисление дисперсии случайной величины.

Согласно этому критерию, количество сохраненной информации равно доле «объясненной» с помощью новых признаков ŋ_1…ŋ_m дисперсии исходных признаков.

Первая главная компонента – это нормированно-центрированная линейная комбинация исходных признаков, которая среди всех прочих нормировано-центрированных линейных комбинаций обладает на данном наборе данных наибольшей дисперсией.

k-ой главной компонентой (k = 2…m) называется такая нормировано-центрированная линейная комбинация исходных признаков, которая не коррелированна с (k-1) предыдущими главными компонентами и среди всех прочих нормированно - центрированных линейных комбинаций, не коррелированных с предыдущими (k-1) главными компонентами обладает на данном наборе данных наибольшей дисперсией.

2. Вычисление главных компонент

Рассмотрим итерационный алгоритм вычисления главных компонент. Возьмем прямую следующего вида:

y=at+b.

Тогда сумма квадратов расстояний от точек наблюдений до вышеуказанной прямой будет равна выражению:

Q=.

Пусть a,- произвольные вектора

Данная сумма- это критерий, минимизируемый с помощью алгоритма:

1. Определяем набор :

2. Определяем новые координаты векторов a и b:

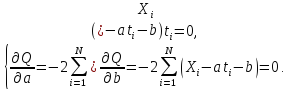
3. Проверяем на останов. Алгоритм прерывается в том случае, если , где𝛥Q – изменение величины Q за итерацию,

𝜀 – малая величина.

Этот способ вычисления первой главной компоненты обладает важным преимуществом: алгоритм обобщается в том случае, если данные содержат неполные значения. Неизвестное значение пропускается. Появляется вектор значения всех координат (иначе, «эффективный» вектор среднего):

Вектор a при полных данных задаст направление первой главной компоненты, а при неполных - «эффективную» первую главную компоненту.

1. Основные числовые характеристики главных компонент

• EZ=E(LX)=L×EX=0

• Ковариационная матрица вектора главных компонент:

L∑

в) Сумма дисперсий исходных признаков равна сумме дисперсий всех главных компонент

г) Обобщенная дисперсия исходных признаков равна обобщенной дисперсии главных компонент

д) «Матрица нагрузок» - это матрица перехода из исходного пространства переменных  в пространство главных компонент.

4. Матрица «нагрузок» главных компонент

Матрица «нагрузок» A = ,i,j = 1,2…,p, главных компонент на исходные признаки тоже одна из важных характеристик главных компонент. Если анализируемые переменные X = (x⁽¹⁾, x⁽²⁾,…,x^(p))^T , которые процентрированы и пронормированы, т. е. если главные компоненты построены для признаков X^*= (x^*(1), x^*(2),…,x^*(p))^T, Ex^*(i)=0, Dx^*(i)=1, i=1,2,...,p, то элементы матрицы «нагрузок» 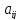определяют степень тесноты линейной связи (по парному коэффициенту корреляции) междуx^*(i) и z^(j) и удельный вес влияния пронормированной j-той главной компоненты на признак x^*(i).

Матрица «нагрузок» А определяется соотношением вида:

, где

=.

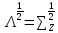Свойства матрицы А:

1. Сумма квадратов элементов любого j-го столбца матрицы А равна дисперсии (j-ой) главной компоненты λ_j.

2. Сумма квадратов элементов любой (i-ой) строки матрицы нагрузок А равна единице.

Данные свойства применимы и для содержательной интерпретации главных компонент.

5. Применение главных компонент

Главные компоненты применяются в решении задач анализа данных. Основные задачи:

1. упрощение, сокращение размерностей анализируемых моделей статистического исследования зависимостей или классификации, что способно облегчить вычисления и интерпретацию статистических выводов;

2. визуализация исходных многомерных данных;

3. предварительная ортогонализация объясняющих переменных используется для устранения мультиколлинеарностью;

4. сокращение статистической информации.

Рассмотрим подробнее одно из распространенных приложений метода главных компонент – визуализацию данных.

Визуализация данных – представление данных в наглядной форме.

Первым выбором в визуализации множества данных является ортогональное проецирование на плоскость первых двух главных компонент. Плоскость проектирования является, по сути плоским двумерным «экраном», расположенным таким образом, чтобы обеспечить «картинку» данных с наименьшими искажениями. Такая проекция будет оптимальна в трех отношениях:

1. Минимальна сумма квадратов расстояний от точек данных до проекций на плоскость первых главных компонент, то есть экран расположен максимально близко по отношению к облаку точек.

2. Минимальна сумма искажений квадратов расстояний между всеми парами точек из облака данных после проецирования точек на плоскость.

3. Минимальна сумма искажений квадратов расстояний между всеми точками данных и их «центром тяжести».