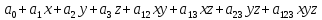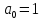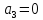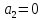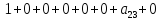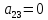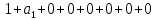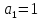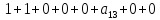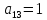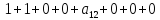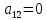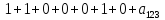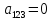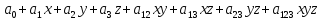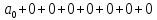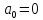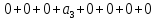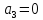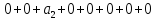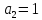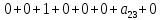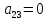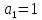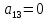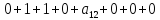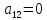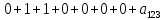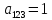Архив2 / курсовая docx525 / kursovaya_diskretka
.docxМинистерство образования Российской Федерации
Орский гуманитарно-технологический институт
(филиал) государственного образовательного учреждения
Высшего профессионального образования
«Оренбургский государственный университет»
Курсовая работа
Орск 2012
Министерство образования Российской Федерации
Орский гуманитарно-технологический институт
(филиал) государственного образовательного учреждения
Высшего профессионального образования
«Оренбургский государственный университет»
Кафедра высшей математики
КУРСОВАЯ РАБОТА
По дисциплине: Дискретная математика
«Многочлен Жигалкина»
Исполнитель: _________ Газизова И.Р.,
студент II курса группы 11ИВТ дневного обучения
Руководитель: _________ Блиялкина Г. П.,
ст. преподаватель кафедры высшей математики
Дата допуска к защите: ____________
_________ «___»___ 2012 г. |
Рег. №____ Лаборант ___________ |
Орск 2012 г.
Содержание
Краткие теоретические сведения о многочлене Жигалкина. 3
Решение. 1 Способ (метод цепочки). 5
Решение. 2 способ (метод неопределенных коэффициентов). 6
Пример решения задач. 7
Список использованной литературы. 8
Краткие теоретические сведения о многочлене Жигалкина.
Для любой функции алгебры логики существует ее представление в виде многочлена Жигалкина.
Причем для системы Жигалкина {+, ^, 1} используются следующие тождества:
x+x=0, x^x=x,
x+x=1, x^x=0,
x+0=x, x^0=0,
x+1=x x^1=x,
Замечание: Знак конъюнкции «^» будем заменять невидимой точкой – умножением.
Определение: Многочленом Жигалкина называется многочлен, являющийся суммой константы и различных одночленов, в которые все переменные входят не выше, чем в первой степени.
Многочлен
Жигалкина константы равен самой
константе:
.
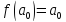Многочлен
Жигалкина функции одной переменной:
.
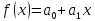Многочлен Жигалкина функции двух переменных:
.
Многочлен Жигалкина функции трех переменных:
.
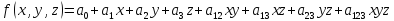Теорема
Жигалкина:
Каждая булева функция
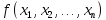может быть представлена в виде многочлена
Жигалкина и притом единственным образом,
с точностью до порядка слагаемых.
Пример решения заданий:
Привести
к виду многочлен Жигалкина функцию
.
Решение. 1 Способ (метод цепочки).
Избавимся от операций «~» и «→» по формулам алгебры логики A~B=AB˅AB, A→B=A˅B.
далее
используем законы де Моргана.
A˅B=A
· B,
AB=A˅B;
=xy(y˅z) · xy(y˅z)˅x˅yz=
=(xy˅(y˅z))(xy˅y˅z)˅x˅yz=
=(x˅y˅y˅z)(xy˅y˅z)˅x˅yz=
В обеих скобках применяем закон полного поглощения A˅AB=A;
=(x˅y)(y˅z)˅x˅yz=
раскроем скобки;
=xy˅xz˅yy˅yz˅x˅yz=
Первое и второе слагаемое поглотит x, третье слагаемое yy=0 (закон противоречия), в четвертом и шестом слагаемых вынесем общий множитель z за скобки;
=x˅z (y˅y) = x˅z=
В скобках (y˅y) = 1 (закон исключения третьего), z·1=z;
Полученный результат подводим под систему Жигалкина и раскрываем скобки;
=xz = x(z+1)+1 = xz+z+1.
Полученное выражение – есть Многочлен Жигалкина.
Решение. 2 способ (метод неопределенных коэффициентов).
Построим таблицу истинности для f(x, y, z)=(xy~(y˅z))→(x˅yz).
|
x |
y |
z |
xy |
y˅z |
xy~(y˅z) |
x |
yz |
x˅yz |
f |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
Построим ещё одну таблицу, в «шапке» которой входящие переменные x, y, z, результирующее f, найденное в предыдущей таблице и стандартное выражение многочлена Жигалкина для трех переменных.
На каждом наборе переменных подставляем в выражение многочлена вместо x, y, z соответствующие значения, учитываем значение f на данном наборе и, используя свойство 1+1=0, последовательно делаем вывод о каждом числовом коэффициенте a.
|
x |
y |
z |
f |
|
Вывод |
|
0 |
0 |
0 |
1 |
|
|
|
0 |
0 |
1 |
1 |
|
|
|
0 |
1 |
0 |
1 |
|
|
|
0 |
1 |
1 |
1 |
|
|
|
1 |
0 |
0 |
0 |
|
|
|
1 |
0 |
1 |
1 |
|
|
|
1 |
1 |
0 |
0 |
|
|
|
1 |
1 |
1 |
1 |
|
|
Таким образом получим f(x, y, z) = 1+x+xz.
Результаты, полученные 1 и 2 способами одинаковы.
Пример решения задач.
Привести к виду многочлен Жигалкина S= (x ~ y ) → xz.
1 способ решения.
S=(x ~ y) → xz = xy ˅ xy ˅ xz = xy · xy · xz =
= (( xy+1 )(( x+1 )( y+1 )+1 )+1 ) ( xz+1 )+1=
= (( xy+1 )( xy + x + y + 1 +1 ) +1 )( xz + 1 ) + 1 =
xy + xy + xy + xy + x + y + 1) ( xz +1 ) + 1 =
= xz + x + xyz + y + xz + 1 + 1 = x + y +xyz .
2 способ решения.
|
x |
y |
z |
x~y |
xz |
S |
|
Вывод |
|
0 |
0 |
0 |
1 |
0 |
0 |
|
|
|
0 |
0 |
1 |
1 |
0 |
0 |
|
|
|
0 |
1 |
0 |
0 |
0 |
1 |
|
|
|
0 |
1 |
1 |
0 |
0 |
1 |
|
|
|
1 |
0 |
0 |
0 |
0 |
1 |
|
|
|
1 |
0 |
1 |
0 |
1 |
1 |
|
|
|
1 |
1 |
0 |
1 |
0 |
0 |
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|
|
S = x + y + xyz
Результаты, полученные 1 и 2 способами, одинаковы.
Список использованной литературы.
-
Акимов О.Е. Дискретная математика: логика, группы, графы. – М: Лаборатория базовых знаний, 2003.
-
Аляев Ю. А., Тюрин С. Ф. Дискретная математика и математическая логика. – М: Финансы и статистика, 2006.
-
Блиялкина Г. Н. Дискретная математика: Методические рекомендации к курсу. – Орск: Издательство ОГТИ, 2004.
-
Галушкина Ю. И., Марьямов А. Н. Конспект лекций по дискретной математике. – М: Айрис – пресс, 2007.
-
Горбатов В. А., Горбатов А.В., Горбатова М. В. Дискретная математика: Учебник для студентов вузов. – М: ООО «Издательство АСТ», ООО «Издательство Астрель»,2003.
-
Канцедал С. А. Дискретная математика: учебное пособие. – М: НД «Форум»: ИНФРА – М, 2007.
-
Нефедов В. Н., Осипова В. А. Курс дискретной математики. – М: Издательство МАИ, 1992.
-
Новиков Ф. А. Дискретная математика для программистов. Учебник для вузов. – СПб: Питер, 2005.