8. Создание регрессионных зависимостей для моделирования и прогнозирования процессов

При экспериментальном исследовании какого-либо явления получаемые данные содержат сведения о законе функционирования системы, а также случайные величины, связанные с ошибками измерения или другими вспомогательными процессами, которые могут появляться и исчезать помимо воли исследователя (помехи, шумы). Поэтому важно выделить функцию отклика, отбросив случайные значения. Функции отклика однопараметрические или многопараметрические являются математической моделью процесса. Для их получения служит регрессионный анализ. Здесь вы должны показать, что освоили методику построения однопараметрических регрессионных зависимостей в Mathcadи их использование для прогнозирования.

Для одной из зависимостей вашей системы у=Ф(х),характеризующей какой либо основной существенно изменяющийся процесс, содержащий не менее 10 значенийхи им соответствующих значенийу, построить различные линии регрессии (полиномиальную (второй и третьей степени), линейную и зависимость в виде суммы различных функций. Величинойх может быть время, ау – параметром от него существенно зависящим. Например: количество заказов, посетителей, вызовов. Кроме этого,хможет быть температура (средняя температура или текущая), аувремя сушки, жарки, количество выпитых напитков, твердость.

Пример построения линейной линий регрессии для двух векторов1

Не забудьте установить нумерацию массивов с единицы. Затем создайте два вектора, содержащие значения аргумента Vxи функцииVy.

1)Вычислите коэффициенты aиbлинейной регрессии для функции видау=a+bx с помощью стандартных функцийintercept() иslope().

2) Создайте свою функцию Flinreg()

3) Создайте ранжированную переменную, содержащую столько компонент, какова размерность векторов Vx, Vy. В данном случае их пять.i:=1..5.

4) Постройте график по двум векторам VxиVy и по полученной функции линейной регрессии. Заметим, что индексы приVx_iвводятся после нажатия левой квадратной скобки на клавиатуре. График для рассмотренного примера приведен на рис. 6.

6) Для оценки достоверности линии регрессии определите коэффициент корреляции с помощью стандартной функции corr(). Чем ближе коэффициент корреляции к единице, тем точнее представленная точками зависимость приближается к линейной.

Рисунок 6 – Экспериментальные данные и линейная линия регрессии

Естественно, что для рассматриваемого вами вектора коэффициент корреляции может быть значительно меньше. Если коэффициент корреляции меньше 0,3 считается, что имеется очень слабая корреляционная связь и степень близости рассматриваемой зависимости к линейной мала.

Пример полиномиальной регрессии

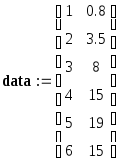1) Пусть зависимостьY=F(x) задается матрицейdata с числом строкn=6, столбцов 2. Выделите из неё вектораXиYисходных данных. Для ввода номеров столбцов используйте панель инструментовМатрицы, выбравM^<>.

Для создания функции регрессии можно использовать полином любой степени, которая не превосходит число строк вектора минус 1. То есть k<=n-1. Остановимся на кубическом полиноме, т. е степень полинома 3, присвоив для этого идентификаторуk:=3. Для получения линии регрессии воспользуемся стандартными функциямиregress()иinterp(). Первая функция возвращает матрицу коэффициентовz, в которой послеk-ой позиции располагаются коэффициенты полинома k-ой степени. Вторая – использует эти коэффициенты для вычисления значения полинома для заданного значениях.

2) Создайте свою функцию fit(), которая позволит определить значение полинома в любой точкеx.

Для построения графика введите две ранжированные переменные. Первая i,максимальное значение, которой равно числу строкn, а вторую j с максимальным значением 50, которое обеспечит плавное построение графика в выбранном диапазоне.

Создадим вектор tдля использования полученного полинома

.

Затем построим график с экспериментальными точками и графиком полинома третьей степени для них (рис. 7).

Спрогнозируйте процесс с помощью функции fit(), для значенийхвне рассмотренного в эксперименте диапазона, в данном случаеfit(8)=

3) Оцените достоверность регрессии, подсчитав различными способами коэффициент достоверности аппроксимации R².

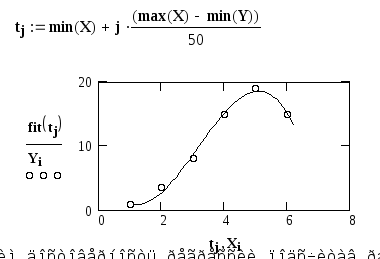
Рисунок 7 – Экспериментальные данные и линия регрессии в виде полинома.

Во втором случае, при вычислении RRэквивалентном R², выражение более лаконичное, так как не используются индексы в знаках сумм, а результат идентичен. Для создания такого выражения проведена векторизация выражений, что позволило отказаться от индексов. Векторизация производится с помощью кнопки меню «Матрицы» .

Учтите, чем ближе величина к единице, тем лучше линия регрессии описывает экспериментальные данные. Однако выбор наилучшей линии регрессии более сложен и не может определяться только величиной. Чем больше степень полинома, тем лучше аппроксимации, но с увеличением числа коэффициентов в уравнении регрессии снижается степень их достоверности. Например, выбрав коэффициент полинома равнымn-1, можно добиться, что функция точно пройдет через все экспериментальные точки. Но мы должны понимать, что в эксперименте всегда есть случайная составляющая, погрешности измерений. Поэтому, выбрав в качестве функции отклика полином высокой степени, мы случайное возводим в закономерное, и потому такая функция не обладает хорошими прогностическими свойствами и будет непрерывно сильно изменяться, если производить дальнейшее накопление экспериментальных данных.

Аналогичным образом получите линию регрессии для полинома второй степени и определите коэффициент достоверности одним из способов. Постройте аналогичный график и сделайте прогнозирование вне пределов экспериментальных значений х.

Учитывая возможность случайного разброса экспериментальных значений в будущем, сделайте предположение и укажите, какой прогноз, по вашему мнению, более достоверен.

Учтите, что выбор линии регрессии производится с учетом надежности коэффициентов линии регрессии, которая производится специальными способами, изучаемыми в эконометрике. Причем надежность коэффициентов обычно тем выше, чем меньше степень полинома при фиксированном числе экспериментов