Архив1 / doc100 / курсовая работа (3)

Министерство образования Республики Беларусь

Белорусский государственный университет информатики и радиоэлектроники

Факультет компьютерных технологий

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе

по курсу «Основы алгоритмизации и программирования»

на тему

« Методы определения корней уравнения»

Выполнил

Студент группы 281012 Р.И. Чернянин

Руководитель работы А.А. Осмоловский

Минск,2011

СОДЕРЖАНИЕ Введение…………………………………………………………………………………….…….. Математическая постановка задачи………………………………………………………… Метод решения задачи…….……………………………………………………………..….. Укрупненная структура программы и описание назначения ее компонент…………..…. Схемы алгоритмов решения задачи и их описание………………………………………... Результаты тестирования разработанной программы…………………………………….. Методика работы пользователя с разработанной программой………………..................... Заключение………………………………………………………………………………………... Список используемых источников…………………………………………………………….… Приложение А. Листинг программы…………………………………………………..…...……

4 5 5 6 6 7 7 8 10 10

Введение

Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.

Если функция f(x) включает в себя тригонометрические или экспоненциальные функции от некоторого аргумента x, то ее уравнение f(x) =0 называется трансцендентным уравнением. Такие уравнения обычно имеют бесконечное множество решений.

Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения выше четвертой степени.

Большинство употребляющихся приближенных методов решения уравнений являются по сути способами уточнения корней. Для их применения необходимо знание интервала изоляции [a,b], в котором лежит уточняемый корень уравнения.

Процесс определения интервала изоляции [a,b], содержащего только один из корней уравнения, называется отделением этого корня.

Процесс отделения корней проводят исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f(x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, т.е. f(a)f(b)<0, то между точками a и b имеется хотя бы один корень уравнения. Если при этом знак функции f'(x) на отрезке [a,b] не меняется, то корень является единственным на этом отрезке.

Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:

1. отделение корней, - т.е. определение интервалов изоляции [a,b], внутри которого лежит каждый корень уравнения;

2. уточнение корней, - т.е. сужение интервала [a,b] до величины равной заданной степени точности eps.

Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:

1. метод половинного деления (метод дихотомии);

2. метод простых итераций;

3. метод Ньютона (метод касательных);

4. метод хорд.

1. Математическая постановка задачи

Целью данного курсового проекта является разработка программы для нахождения корней нелинейных уравнений. Из всех возможных способов нахождения корней были для реализации были выбраны:

- метод половинного деления (метод дихотомии);

- метод простых итераций;

- метод Ньютона (метод касательных);

- метод хорд.

Рассмотрим основные этапы приведенных методов нахождения корней нелинейного уравнения.

Метод половинного деления.

Краткий алгоритм.

1. В первую очередь нужно разделить интервал, в котором надо найти корни, пополам.

2. Выбираем из двух получившихся интервалов тот, на концах которого функция имеет разные знаки.

3. Проверяем, длина интервала больше заданной точности или нет. Если больше, то возвращаемся к выполнению первого пункта.

4. Если меньше, то он и является решением

Рассмотрим подробнее.

Дано нелинейное уравнение:

(1.1)

Найти корень уравнения, принадлежащий интервалу [a,b], с заданной точностью 

Для уточнения корня методом половинного деления последовательно осуществляем следующие операции:

1. Делим интервал пополам:

(1.2)

2. В качестве нового интервала изоляции принимаем ту половину интервала, на концах которого функция имеет разные знаки

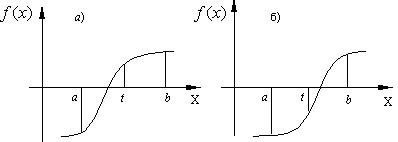
Рис. 1.1

Для этого:

a) Вычисляем значение функции f(x) в точках a и t.

b) Проверяем: если f(a)f(t) < 0, то корень находится в левой половине интервала [a,b] (рис.1.а). Тогда отбрасываем правую половину интервала и делаем переприсвоение b=t.

c) Если f(a)f(t) < 0 не выполняется, то корень находится в правой половине интервала [a,b] (рис.1.б). Тогда отбрасываем левую половину и делаем переприсвоение a=t. В обоих случаях мы получим новый интервал [a,b] в 2 раза меньший предыдущего.

3. Процесс, начиная с пункта 1, циклически повторяем до тех пор, пока длина интервала [a,b] не станет равной либо меньшей заданной точности, т.е.

(1.3)

Пример.  Методом половинного деления уточнить корень уравнения

f(x) = x4 + 2 x3 - x - 1 = 0 , лежащий на отрезке [ 0, 1] .

Последовательно имеем:

f(0) = - 1; f(1) = 1; f(0,5) = 0,06 + 0,25 - 0,5 - 1 = - 1,19;

f(0,75) = 0,32 + 0,84 - 0,75 - 1 = - 0,59;

f(0,875) = 0,59 + 1,34 - 0,88 - 1 = + 0,05;

f(0,8125) = 0,436 + 1,072 - 0,812 - 1 = - 0,304;

f(0,8438) = 0,507 + 1,202 - 0,844 - 1 = - 0,135;

f(0,8594) = 0,546 + 1,270 - 0,859 - 1 = - 0,043 и т. д.

Можно принять

x = (0,859 + 0,875) = 0,867

Метод простых итераций.

Краткий алгоритм.

1. Исходное уравнение f(x)=0 приводят к виду x=f(x).

2. Любую точку из интервала считаем начальным приближением.

3. От этой точки производят вычисление икса с заданным шагом, пока |x(n) - x(n-1)| не будет меньше заданной точности, либо пока число итераций не превысит некоторое заданное число.

Рассмотрим подробнее.

В ряде случаев весьма удобным приемом уточнения корня уравнения является метод последовательных приближений (метод итераций).

Пусть с точностью  необходимо найти корень уравнения f(x)=0, принадлежащий интервалу изоляции [a,b]. Функция f(x) и ее первая производная непрерывны на этом отрезке.

Для применения этого метода исходное уравнение f(x)=0 должно быть приведено к виду

(1.4)

В качестве начального приближения 0 выбираем любую точку интервала [a,b].

Далее итерационный процесс поиска корня строится по схеме:

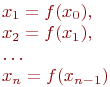(1.5)

В результате итерационный процесс поиска реализуется рекуррентной формулой (1.5). Процесс поиска прекращается, как только выполняется условие

(1.6)

или число итераций превысит заданное число N.

Для того, чтобы последовательность х₁, х₂,…, х_n приближалась к искомому корню, необходимо, чтобы выполнялось условие сходимости:

(1.7)

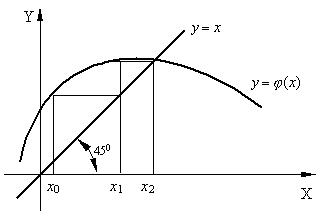
Рис. 1.2 -  Геометрический смысл метода

Метод Ньютона (метод касательных);

Краткий алгоритм

1. Выбираем начальную точку в конце интервала.

2. Проводим к ней касательную

3. Пересечение касательной с осью Х дает первое значение корня х1.

Рассмотрим подробнее.

Метод Ньютона относится к градиентным методам, в которых для нахождения корня используется значение производной.

Дано нелинейное уравнение:

f(x)=0

Найти корень на интервале [a,b] с точностью .

Метод Ньютона основан на замене исходной функции f(x), на каждом шаге поиска касательной, проведенной к этой функции. Пересечение касательной с осью Хдает приближение корня (Рис. 1.3).

Выберем начальную точку x₀=b (конец интервала изоляции). Находим значение функции в этой точке и проводим к ней касательную, пересечение которой с осью Хдает нам первое приближение корня x₁.

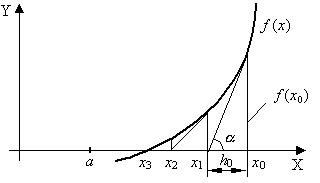
Рис. 1.3

x₁ = x₀ – h₀,

где

(1.8)

Поэтому

(1.9)

В результате итерационный процесс схождения к корню реализуется рекуррентной формулой

(1.10)

Процесс поиска продолжаем до тех пор, пока не выполнится условие:

(1.11)

Упростим условие (1.11), исходя из (1.10). Получим:

(1.12)

Метод обеспечивает быструю сходимость, если выполняется условие:

(1.13)

т.е. первую касательную рекомендуется проводить в той точке интервала [a,b], где знаки функции f(x₀) и ее кривизны f"(x₀) совпадают.

Метод хорд

Краткое описание.

Метод основан на замене функции f(x) на каждом шаге поиска хордой, пересечение которой с осью Х дает приближение корня. Семейство хорд может строиться:

а) при фиксированном левом конце хорд, т.е. z=a, тогда начальная точка х₀=b;

б) при фиксированном правом конце хорд, т.е. z=b, тогда начальная точка х₀=a.

Рассмотрим подробнее.

В данном методе процесс итераций состоит в том, что в качестве приближений к корню уравнения принимаются значения х₁, х₂, ..., х_n точек пересечения хорды АВ с осью абсцисс. Сначала запишем уравнение хорды AB:

. (1.14)

Для точки пересечения хорды AB с осью абсцисс (х = х₁, y = 0) получим уравнение:

(1.15)

Пусть для определенности f'' (x) > 0 при а   х   b (случай f'' (x) < 0 сводится к нашему, если записать уравнение в виде - f(x) = 0). Тогда кривая у = f(x) будет выпукла вниз и, следовательно, расположена ниже своей хорды АВ. Возможны два случая: 1) f(а) > 0 (Рис. 1.4, а) и 2) f(b) < 0 (Рис. 1.4, б).

   

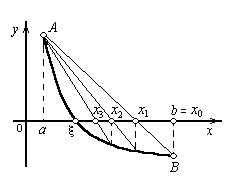
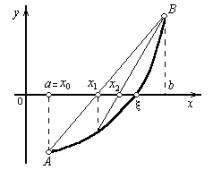
Рис. 1.4, а, б.

 

В первом случае конец а неподвижен и последовательные приближения: x₀ = b;

(1.16)

образуют ограниченную монотонно убывающую последовательность, причем

(1.17)

Во втором случае неподвижен конец b, а последовательные приближения: x₀ = а;

(1.18)

образуют ограниченную монотонно возрастающую последовательность, причем

(1.19)

Обобщая эти результаты, заключаем:

1. неподвижен тот конец, для которого знак функции f (х) совпадает со знаком ее второй производной f'' (х);

2. последовательные приближения x_n лежат по ту сторону корня x , где функция f (х) имеет знак, противоположный знаку ее второй производной f'' (х).

Итерационный процесс продолжается до тех пор, пока не будет обнаружено, что

| x_i - x_{i -} 1|< e , (1.20)

где e - заданная предельная абсолютная погрешность.

Пример. Найти положительный корень уравнения

f(x) = x³ - 0,2 x² - 0,2 х - 1,2 = 0

с точностью e = 0,01.

Прежде всего, отделяем корень. Так как

f (1) = -0,6 < 0 и f (2) = 5,6 > 0,

то искомый корень x лежит в интервале [1, 2]. Полученный интервал велик, поэтому разделим его пополам. Так как

f (1,5) = 1,425 > 0, то 1< x < 1,5.

Так как f'' (x) = 6 x - 0,4 > 0 при 1 < х < 1,5 и f (1,5) > 0, то воспользуемся формулой (1.16) для решения поставленной задачи:

= 1,15;

|x₁ - x₀| = 0,15 > e ,

следовательно, продолжаем вычисления;

f (х₁) = -0,173;

= 1,190;

|x₂ - x₁| = 0,04 > e ,

f (х₂) = -0,036;

= 1,198;

|x₃ - x₂| = 0,008 < e .

Таким образом, можно принять x = 1,198 с точностью e = 0,01.

Заметим, что точный корень уравнения x = 1,2.

 

2. Метод решения задачи.

При решении поставленной задачи оптимально использовать для представления информационных материалов язык Delphi, который является языком высокого уровня и позволяет быстро и эффективно создавать приложения, с использованием графической библиотеки OpenGL .

Для реализации оценки сложности программы была выбрана система программирования Delphi версии 7 фирмы Enterprise (Borland), так как она предоставляет наиболее широкие возможности для программирования приложений ОС Windows.

Delphi – это продукт Borland International для быстрого создания приложений. Высокопроизводительный инструмент визуального построения приложений включает в себя настоящий компилятор кода и предоставляет средства визуального программирования, несколько похожие на те, что можно обнаружить в Microsoft Visual Basic или в других инструментах визуального проектирования. В основе Delphi лежит язык Object Pascal, который является расширением объектно-ориентированного языка Pascal. В Delphi также входят генераторы отчетов, библиотеки визуальных компонентов, то есть все необходимое для профессиональной разработки информационных систем или просто программ для Windows-среды.

Преимущества Delphi по сравнению с аналогичными программными продуктами.

– быстрота разработки программного средства;

– высокая производительность разработанного приложения;

– низкие требования разработанного программного средства к ресурсам компьютера;

– наращиваемость за счет встраивания новых компонент и инструментов в среду Delphi;

– возможность разработки новых компонент и инструментов собственными средствами Delphi (существующие компоненты и инструменты доступны в исходных кодах);

– удачная проработка иерархии объектов.

Система программирования Delphi рассчитана на программирование различных приложений и предоставляет большое количество компонентов для этого, как, например, неотъемленный компонент курсового проекта OpenGL.

OpenGL является одним из самых популярных прикладных программных интерфейсов (API – Application Programming Interface) для разработки приложений в области двумерной и трехмерной графики.

Характерными особенностями OpenGL, которые обеспечили распространение и развитие этого графического стандарта, являются:

Стабильность. Дополнения и изменения в стандарте реализуются таким образом, чтобы сохранить совместимость с разработанным ранее программным обеспечением.

Надежность и переносимость. Приложения, использующие OpenGL, гарантируют одинаковый визуальный результат вне зависимости от типа используемой операционной системы и организации отображения информации. Кроме того, эти приложения могут выполняться как на персональных компьютерах, так и на рабочих станциях и суперкомпьютерах.

К тому же высокие скорость и качество создания программного средства может обеспечить только среда визуального проектирования, способная взять на себя значительные объемы рутинной работы по подготовке программного средства. Возможности Delphi полностью отвечают требованиям данного курсового проекта, а также подходят для создания систем любой сложности.

Входной информации в данной программе являются введенные уравнения, интервал, на котором производится поиск решения, и шаг, то есть точность проверки. Значения шага и интервала могут быть любыми числами (шаг больше нуля), уравнение вводится по определенным правилам. Для упрощения проверки курсовой работы по умолчанию в каждом поле уже присутствуют данные, удовлетворяющие условию работы программы.

В уравнении допускается использование круглых скобок, причем количество открывающихся и закрывающихся скобок должно быть одинаковым, иначе произойдет ошибка при вычислениях. Арифметические операции записываются обычным способом, то есть +(сложение), -(вычитание), *(умножение), /(деление).

Для возведения в степень используется символ ^, например x^3. Допускается введение таких тригонометрических функций, как синус (sin), косинус (cos), тангенс (tg), а так же десятичного(lg) и натурального(ln) логарифмов.

Выходной информацией при выборе любого из методов решения нелинейных уравнений является значение корня уравнения x. Чтобы получить его значение, необходимо после введения всех необходимых начальных данных нажать кнопку «%Решить%». В появившемся окне будут так же отображаться промежуточные результаты вычислений. По нажатию на кнопку «Далее» происходит один шаг выполнения операций. Когда вычисления приобретут необходимую точность, в окне появится надпись «Конец решения» и ниже значение самого корня в формате x= «число»

Если мы не знаем точно интервал, в котором находится корень уравнения, мы можем нажать «Найти а=, b= и %Решить%». При этом на первом шаге программа вычислит необходимые границы интервала для нахождения корня уравнения. При нажатии на «Далее», в появившемся окне, будут отображаться промежуточные результаты вычислений. По нажатию на кнопку «Далее» происходит один шаг выполнения операций. Когда вычисления приобретут необходимую точность, в окне появится надпись «Конец решения» и ниже значение самого корня в формате x= «число»

Во всех методах, кроме метода итераций, можно найти значение функции при заданном значении x. Для этого необходимо, при всех необходимых заполненных полях в верхней области окна, ввести значение x в поле «х=» и нажать кнопку «Найти». Справа от кнопки появится значение функции при заданном значении x.

Так же, независимо от выбранного метода решения, мы можем вывести на экран все значения записанной функции в заданном пользователем интервале с определенной величиной интервала.

2. Укрупненная структура программы и описание назначения ее компонент.

Данная программа может применяться как в ознакомительных целях в рамках курсового проекта, так и в учебных, так как методы нахождения корней уравнения, приведенные в курсовом проекте, являются достаточно точными и проверенными.

16