4. Метод Монте-Карло

В математике существует целое направление, связанное с методом Монте-Карло. Оно занимается использованием случайных чисел для решения различных математических задач: интерполяции, вычисления интегралов, решения дифференциальных и интегральных уравнений, решения систем линейных уравнений, поиска экстремума, моделирования процессов и т. д. [1]

Одно из преимуществ метода Монте-Карло заключается в его своеобразной "локальности": этим методом можно, например, искать одну составляющую решения системы линейных уравнений, не интересуясь другими компонентами, или искать значение функции, являющейся решением дифференциального уравнения, в одной точке и т. п. Если, например, трудоемкость прямых методов вычисления определенных интегралов с ростом размерности п пространства переменных возрастает как kⁿ (k — число шагов, на которое разбивается интервал интегрирования по каждой оси), то трудоемкость алгоритма Монте-Карло возрастает как kⁿ/2.

Основной недостаток метода Монте-Карло — сравнительно медленная сходимость, для получения более или менее надежных результатов требуется большое число повторений.

Проиллюстрируем идеи метода Монте-Карло на примере вычисления определенного интеграла от функции, зависящей от одной переменной. [4] Пусть нам необходимо вычислить интеграл от некоторой заданной функции f(x) на интервале [а,Ь] (формула (2)). В предыдущем разделе мы рассмотрели несколько различных формул интегрирования, в которых использовались значения функции f(x), вычисляемые в равноотстоящих точках. Однако можно использовать и другой подход, суть которого легко понять из сле­дующего примера.

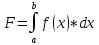(2)

Представим себе прямоугольник высотой Н и длиной b - а, такой, что функция f(x) целиком лежит внутри данного прямоугольника (рис. 11.4).

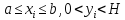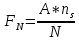Сгенерируем N пар случайных чисел равномерно распределенных в данном прямоугольнике:.Тогда доля точек (x_i, у_i), удовлетворяющих условию y_i ≤ f(x_i) являет­ся оценкой отношения интеграла от функции f(x) к площади рассматри­ваемого прямоугольника. Следовательно, оценка интеграла в данном методе может быть получена по формуле (3) :

(3)

где n_s — число точек, удовлетворяющих условию y_i ≤ f(x_i) , N — полное ко­личество точек, А — площадь прямоугольника.

В пакете MATLAB описанный алгоритм реализуется следующей последовательностью команд:

% координаты нижнего левого угла прямоугольника

» X min=0;

» Ymin=0;

% координаты правого верхнего узла прямоугольника

» Xmax=pi/2;

» Ymax=1.5;

» N=1000; % число точек случайной последовательности

% вычисление последовательности случайных чисел равномерно

% распределенных на интервале [Xmin,Xmax]

»for i=l:N

x(i)=Xmin+(Xmax-Xmin)*rand(l);

end;

% вычисление последовательности случайных чисел равномерно % распределенных на интервале [Ymin.Ymax]

»for i=l:N

y(i)=Ymin+(Ymax-Ymin)*rand(l);

end;

» f=inline('sin(x)', 'x');% задание подынтегральной функции

% подсчет точек, лежащих ниже графика функции f(x)

»for i=l:N

If f(x(i))>=y(i)

s(i)=l;

else

s(i)=0;

end;

end;

»S=sum(s);

» A=(Xmax-Xmin)*(Ymax-Ymin); % площадь прямоугольника

» A*S/N % % вычисление значения интеграла

ans = 1.0344

В приведенной выше последовательности команд мы использовали функцию inline, которая преобразует первый аргумент функции, являю­щийся строковым выражением, в описание функции, зависящей от пере­менных, стоящих на втором и последующих местах в списке формальных параметров функции. Например, для задания функции F(x,y) = sin(x+y) не­обходимо ввести следующую команду:

» F=inline('sin(x+y)V, 'у')

Есть и другие способы применения метода Монте-Карло, описанные в источниках [1],[4].