Тема 6 Транспортная задача

В настоящее время транспортная задача линейного программирования широко применяется как в теоретических разработках, так и в практике планирования различных экономических процессов. Особенно важное значение она имеет при решении вопросов рационализации поставок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта. Она применяется и при решении экономических проблем, которые по своему характеру не имеют ничего общего с транспортировкой груза, например, оптимальное закрепление за станками операций по обработке деталей ("станковая" задача), проблема выбора (оптимального назначения), задачи размещения производства с учетом транспортных и производственных затрат.

В общем виде постановка транспортной задачи такова. (Сейчас рассматривается классическая постановка задачи, ее применение к станковой задаче рассмотрим позже).

Пусть некоторый однородный продукт, сосредоточенный у m поставщиков A_i в количестве a_i(i=1,2,…,m) единиц соответственно, необходимо доставить n потребителям B_j в количестве b_j() единиц. Известна стоимость c_ij перевозки единицы груза от i-го поставщика к j-му потребителю. Необходимо составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребность и имеющий минимальную стоимость.

Обозначим через x_ij количество единиц груза, запланированных к перевозке от i-го поставщика к j-му потребителю; тогда условие задачи можно записать в виде таблицы, которую в дальнейшем будем называть матрицей планирования (см. табл. 6.1).

Таблица 6.1

Поставщики	Потребители				Запасы
	B1	B2	...	Bn
A1	x11 С11	x12 C12	...	x1n C1n	a1
A2	x21 C21	x22 C22	...	x2n C2n	a2
...	...	...	...	...	...
Am	xm1 Cm1	xm2 Cm2	...	xmn Cmn	am
Потребности	b1	b2	…	bn	∑ai=∑bj

Составим математическую модель задачи. Так как от -го поставщика к-му потребителю запланировано к перевозкеединиц груза, то стоимость перевозки составит. Стоимость всего плана выразится двойной суммой.

Систему ограничений получаем из следующих условий задачи:

а) все грузы должны быть вывезены, т.е. ()

(уравнения получаются из строк таблицы);

б) все потребности должны быть удовлетворены, т.е. () (уравнения получаются из столбцов таблицы).

Таким образом, математическая модель транспортной задачи имеет следующий вид.

Найти наименьшее значение линейной функции при ограничениях

В рассмотренной модели может быть два случая, когда суммарные запасы равны суммарным потребностям, т.е. и когда не равны. В первом случае транспортная модель задачи называетсязакрытой, во втором – открытой.

Когда суммарные запасы не равны суммарным потребностям, может быть два случая:

а) суммарные запасы превышают суммарные потребности ;

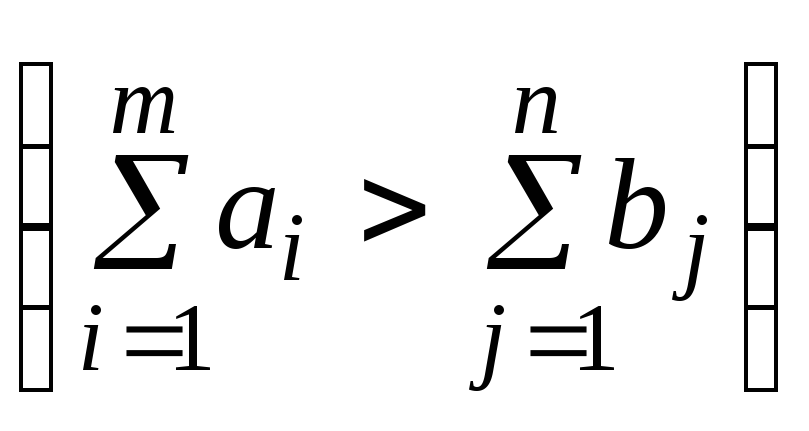б) суммарные потребности превышают суммарные запасы .

Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений.

В случае (а) ограничения имеют вид:

В случае (б) ограничения имеют вид:

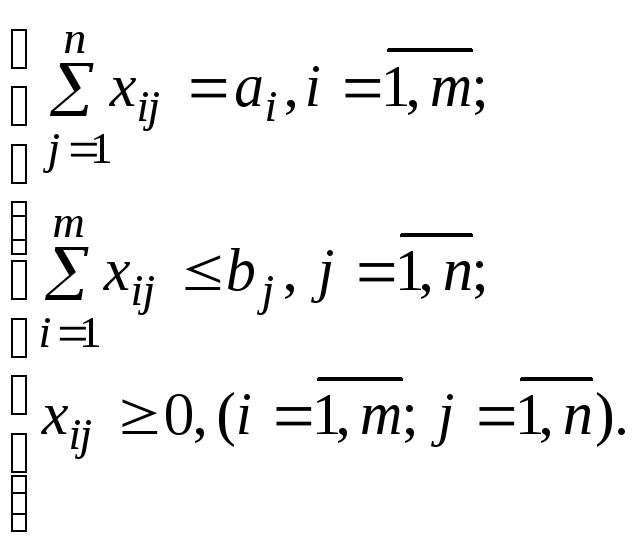
Открытая модель приводится к закрытой модели.

В случае (а), когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель потребности которогоВ случае (б), когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщикзапасы которого

Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными 0, т.к. в обоих случаях груз не перевозится. После преобразований задача принимает вид закрытой модели. Так что прежде чем решать какую-нибудь транспортную задачу, необходимо сначала проверить, к какому виду модели она принадлежит, только после этого решать.

Существует следующая теорема.

Любая транспортная задача, у которой суммарный объем запасов совпадает с суммарным объемом потребностей, имеет решение.

Особенности транспортной задачи по сравнению с общей задачей линейного программирования вытекают из ее математической модели: целевая функция имеет несколько другой вид (двойная сумма), вид коэффициентов специфический (там, где будет перевозка, коэффициент будет равен 1, в остальных - 0, т.е. в каждом столбце будет две единицы, остальные элементы - нули). Методы решения транспортной задачи в силу этих особенностей отличны от методов решения задачи линейного программирования. Их мы рассмотрим позже.

Ранее представленная станковая задача полностью попадает под рассматриваемую модель транспортной задачи, если принять другой экономический смысл переменных. В самом деле, пусть на предприятии имеется m видов станков, максимальное время работы которых соответственно равно a_i (i=) часов. Каждый из станков может выполнять n видов операций. Суммарное время выполнения каждой операции соответственно равно b_j (j=) часов. Известна производительность (c_ij) i-го станка при выполнении j-й операции. Определить, сколько времени и на какой операции нужно использовать каждый из станков, чтобы обработать максимальное количество деталей.

Для составления математической модели обозначим через x_ij (i=,j=) время, которое i-й станок должен работать на j-й операции. Тогда количество деталей, обработанных на i-м станке, равно c_ijx_ij.. Количество деталей, обработанных на всех станках, можно выразить функцией .

Так как максимально возможное время работы i-го станка ограничено (значением a_i), то получаем ,(), если максимальное время работы станков используется полностью, или , если это время используется не полностью.

С другой стороны, время, отведенное на j-ю операцию, равно b_j часов, поэтому . Из условия следует, что общее время работы всех станков должно быть равно сумме максимальных времен работы всех станков, т.е., и времени, необходимого на выполнение всех операций, т.е.. Отсюда следует, что.

Таким образом, необходимо найти максимальное значение линейной функции при ограничениях

Для того, чтобы решить эту задачу методом потенциалов, достаточно линейную функцию умножить на , т.е. считать в таблице матрицы планирования все значенияc_ij отрицательными (в транспортной задаче, как известно, целевая функция должна быть на минимум).

Построение первоначального опорного плана

Как и для других задач линейного программирования, итерационный процесс по отысканию оптимального плана транспортной задачи начинают с нахождения опорного плана.

Рассмотрим систему ограничений транспортной задачи. Она содержит неизвестных иуравнений, связанных соотношениемт.е., если сложить почленно уравнения отдельно подсистемыи отдельно подсистемы, то получим два одинаковых уравнения. Наличие в системе ограничений двух одинаковых уравнений говорит об ее линейной зависимости. Если одно из этих уравнений отбросить, то в общем случае система ограничений должна содержатьлинейно независимых уравнений. Следовательно, опорный план транспортной задачи может иметь не болееотличных от0 неизвестных, или перевозок. Это важно для понимания.

Если в опорном плане число отличных от нуля компонент в точности равно , то план является невырожденным, а если меньше – то вырожденным. Таким образом, если каким-либо способом получен невырожденный опорный план транспортной задачи, то в матрице() () значений его компонент положительными являются только , а остальные равны нулю.

Если условие транспортной задачи и ее опорный план записаны в виде таблицы, то клетки, в которых находятся отличные от нуля перевозки, называются занятыми, остальные – незанятыми. Занятые клетки соответствуют базисным неизвестным, и для невырожденного опорного плана их количество равно . Если ограничения транспортной задачи записаны в виде двух подсистем уравнений, то, как известно, базисным неизвестным, включенным в опорный план, соответствует система линейно независимых векторов. Опорность плана при записи условий транспортной задачи в виде таблицы заключается в егоацикличности, т.е. в таблице нельзя построить замкнутый цикл, все вершины которого лежат в занятых клетках.

Циклом называется набор клеток, в котором две и только две соседние клетки расположены в одном столбце или одной строке таблицы, причем последняя клетка находится в той же строке или столбце, что и первая. Построение циклов начинают с какой-либо занятой клетки и переходят по столбцу (строке) к другой занятой клетке, в которой делают поворот под прямым углом и движутся по строке (столбцу) к следующей занятой клетке и т.д., пытаясь возвратиться к первоначальной клетке (см. рис. 16). Если такой возврат возможен, то получен цикл, и план не является опорным. В противном случае план является опорным. Клетки, в которых происходит поворот под прямым углом, определяют вершины цикла.

Для определения опорного первоначального плана существует несколько методов. Рассмотрим два из них: метод северо-западного угла и с учетом наименьших затрат.

Рис. 16. Возможные виды циклов в матрице планирования транспортной задачи

Сущность этих методов, как и других, состоит в том, что опорный первоначальный план находят последовательно за шагов, на каждом из которых в таблице условий задачи заполняют одну клетку, которая становится занятой. Лучше пояснить каждый метод примером.

В методе северо-западного угла при нахождении опорного первоначального плана транспортной задачи на каждом шаге рассматривают первый (сверху) из оставшихся пунктов отправления и первый (слева) из оставшихся пунктов назначения. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного x₁₁ ("северо-западный угол") и заканчивается правой нижней клеткой для неизвестного x_mn, т.е. идет как бы по диагонали таблицы.

Таблица 6.2

Пункты	Пункты назначения					Запасы
отправления	B1	B2	B3	B4	B5
A1	2	3	4	2	4	140
A2	8	4	1	14	1	180
A3	9	7	3	7	2	160
Потребности	60	70	120	130	100	80

Пусть дана транспортная задача, условия которой заданы матрицей планирования, представленной в таблице 6.2. Здесь число пунктов отправления m=3, а число пунктов назначения n=5. Следовательно, опорный план задачи определяется числами, стоящими в 5+3-1=7 заполненных клетках. Заполнение таблицы начинаем с клетки для неизвестного x₁₁, несмотря на стоимость перевозки, т.е. попытаемся удовлетворить потребности первого пункта назначения за счет запасов первого пункта отправления.

Таблица 6.3

	В1	В2	В3	В4	В5
А1	60 2	70 3	10 4	2	4	140
А2	8	4	110 1	70 14	1	180
А3	9	7	3	60 7	100 2	160
Потребности	60	70	120	130	100	480

Так как запасы пункта A₁ больше, чем потребности пункта B₁, полагаем x₁₁=60, записываем это значение в соответствующей клетке таблицы и временно исключаем из рассмотрения столбец B₁, считая при этом запасы пункта A₁ равными . Рассмотрим первые из оставшихся пунктов отправленияA₁ и назначения B₂. Запасы пункта A₁ больше потребностей пункта B₂. Положим x₁₂=70, запишем это значение в соответствующей клетке таблицы и временно исключим из рассмотрения столбец B₂. В пункте A₁ запасы считаем равными единиц. Снова рассматриваем первые из оставшихся пунктов отправленияA₁ и назначения B₂. Потребности пункта B₃ больше оставшихся запасов пункта A₁. Положим x₁₃=10 и исключим из рассмотрения строку A₁. Значение x₁₃=10 запишем в соответствующую клетку таблицы и считаем потребности пункта B₃ равными 110 единицам. Теперь перейдем к заполнению клетки для неизвестного x₂₃ и т.д. Через шесть шагов остается один пункт отправления A₃ с запасом груза единиц и один пункт назначенияB₅ с потребностью единиц. Соответственно имеется одна свободная клетка, которая и заполняется, полагаяx₃₅=100.

В результате получаем опорный план

.

Согласно данному плану перевозок, общая стоимость перевозок составляет

Опорный ли план получен, узнать можно, если, начиная движение от занятой клетки x₁₁ вернуться не только в неё, но и в любую другую занятую клетку, двигаясь только по занятым клеткам, невозможно. В приведённом примере план является опорным.

При составлении первоначального опорного плана методом северо-западного угла стоимость перевозки единицы груза не учитывалась, поэтому построенный план далек от оптимального. Если при составлении опорного плана учитывать стоимость перевозки единицы груза, то, очевидно, план будет значительно ближе к оптимальному.

Метод минимальной стоимости

Суть метода состоит в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел a_i или b_j. Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают пока все запасы не будут распределены, а потребности удовлетворены.

Составим с помощью этого метода опорный план уже рассмотренной задачи. Выбираем в таблице наименьшую стоимость (эта стоимость, помещенная в клетке A₂B₃). Помещаем туда единиц. Исключаем из рассмотрения 3-й столбец и распределим дальше, пока все запасы не будут распределены, а потребности удовлетворены.

Таблица 6.4

	В1	В2	В3	В4	В5	Запасы
А1	60 2	70 3	4	10 2	4	140
А2	8	4	120 1	14	60 1	180
А3	9	7	3	120 7	40 2	160
Потребности	60	70	120	130	100	480

В результате получаем план: X=(x₁₁=60, x₁₂=70, x₁₄=10, x₂₃=120, x₂₅=60, x₃₄=120, x₃₅=40), остальные переменные равны нулю. План не содержит циклов и состоит из семи положительных перевозок, следовательно, является невырожденным опорнымпланом. Определим его стоимость:

(единиц).

Общая стоимость уменьшилась. Этот метод дает более близкий к оптимальному план, чем метод северо-западного угла. Еще существуют такие методы построения первоначального опорного плана, как метод двойного предпочтения, метод аппроксимации Фогеля.

Опорный первоначальный план имеется. Теперь для получения оптимального плана используем метод потенциалов (модифицированный распределительный метод).

Теорема. Если план транспортной задачи является оптимальным, то ему соответствует система изчисели, удовлетворяющих условиям

для

и для.

Числа иназываются потенциалами соответственно поставщиков и потребителей.

На основании этой теоремы для того, чтобы первоначальный опорный план был оптимальным, необходимо выполнение следующих условий:

а) для каждой занятой клетки сумма потенциалов должна быть равна стоимости единицы перевозки, стоящей в этой клетке:

б) для каждой незанятой клетки сумма потенциалов должна быть меньше или равна стоимости единицы перевозки, стоящей в этой клетке:

.

Соотношения представляют собой системулинейных уравнений снеизвестными. Эта система всегда совместна, причём одно из неизвестных можно положить равным любому числу (обычно приравнивают к нулю) и тогда все остальные неизвестные определятся однозначно.

Если хотя бы одна незанятая клетка не удовлетворяет условию , то опорный план является неоптимальным и его можно улучшить, вводя в базис вектор, соответствующий клетке, для которой нарушается условие оптимальности (т.е. в клетку надо переместить некоторое количество единиц груза).

Таким образом, для проверки плана на оптимальность необходимо сначала построить систему потенциалов.

Рассмотрим алгоритм метода потенциалов и одновременно проиллюстрируем его применение на опорном плане, полученном в таблице. Для этого к таблице добавим строку и столбец, в которых записывают значения потенциалов. Алгоритм метода потенциалов состоит в следующем:

1. Построение опорного плана методом северо-западного угла или с учетом наименьших затрат. Этот этап уже выполнен.

2. Построение системы потенциалов. Для этого используем условие для занятых клеток. Систему потенциалов можно построить только для невырожденного опорного плана. Для него систему потенциалов строим, как мы уже говорили, следующим образом. Когда опорный план вырожденный, для устранения этого дополняют количество занятых клеток до, вводя нулевые перевозки. Клетки, в которые введены нулевые перевозки, называютсяфиктивно занятыми. Целесообразно сделать фиктивно занятой клетку, в которой стоит наименьшая стоимость, но так, чтобы сохранилась ацикличность. Фиктивно занятую клетку делаем в той строке или столбце, оценки (потенциалы) которых неизвестны. После того, как построена система потенциалов (см. табл. 6.5 на след.с.), переходим к третьему этапу.

3. Проверка выполнения условия оптимальности для незанятых клеток. Просматриваем строки таблицы и для каждой незанятой клетки проверяем выполнение условия . Если это условие для всех незанятых клеток выполнится, то план оптимальный. Для каждой клетки, в которой не выполняется условие оптимальности, находим величину разницыи записываем ее значения в левый нижний угол этой же клетки. Таких клеток две: (2,2) и (3,2). Разности равны 3 и 1 (см. табл. 6.5).

4. Выбор клетки, в которую необходимо послать перевозку. Загрузке подлежит в первую очередь клетка, которая соответствует т.к. в общей задаче линейного программирования в базис включается тот вектор (если отождествить занятые клетки с векторами, составляющими базис, а незанятые – с остальными векторами системы ограничений), которому соответствуетmax . У нас . Необходимо определить, сколько единиц груза должно быть перераспределено.

Таблица 6.5

Матрица планирования		B1	B2	B3	B4	B5	Запасы
Постав-щики	vj ui	v1=2	v2=3	v3=-3	v4=2	v5=-3
A1	u1=0	60 2	70 _ 3	4	10 + 2	4	140
A2	u2=4	8	 + 4	120 1	14	60 _ 1	180
A3	u3=5	9	 7	3	120 _ 7	40 + 2	160
Потребности		60	70	120	130	100	480

5. Построение цикла и определение величины перераспределения груза. Для определения количества единиц груза, подлежащих перераспределению, отмечаем знаком ''+'' незанятую клетку, которую надо загрузить. Это означает, что клетка присоединяется к занятым клеткам, т.е. включаем в базис. В таблице занятых клеток стало , поэтому появляется цикл, все вершины которого, за исключением клетки, отмеченной ''+'', находятся в занятых клетках, причём этот цикл единственный. Отыскиваем цикл. Его вид может быть разным (см. рис. 16 на с. 87). Они могут быть самопересекающимися, но точки пересечения – не вершины.

Начинаем движение от клетки, отмеченной знаком "+", и, двигаясь по циклу, поочередно проставляем знаки "-", "+" в вершинах цикла. Затем находим , где– величины перевозок, стоящие в вершинах цикла, отмеченные знаком "-". У нас это. Величинаопределяет, сколько единиц груза можно перераспределить по найденному циклу. Значениезаписываем в незанятую клетку, отмеченную знаком "+", двигаясь по циклу, вычитаемиз объёмов перевозок, расположенных в клетках, которые отмечены знаком "-", и прибавляем к объемам перевозок, находящиеся в клетках, отмеченных знаком "+". Еслисоответствует несколько минимальных перевозок, то при вычитании оставляем в соответствующих клетках нулевые перевозки в таком количестве, чтобы во вновь полученном опорном плане занятых клеток было. В результате перераспределенияполучим новый опорный план (неврожденный), который снова подлежит проверке на оптимальность (см. табл. 6.6).

Таблица 6.6

Матрица планирования		B1	B2	B3	B4	B5	Запасы
Постав-щики	vj ui	v1=2	V2=3	v3=0	v4=2	v5=-3
A1	u1=0	60 2	10 _ 3	4	70 + 2	4	140
A2	u2=1	8	+ 4	120 _ 1	14	1	180
A3	u3=5	9	 7	+  3	60 _ 7	100 2	160
Потребности		60	70	120	130	100	480

Вновь строим систему потенциалов и проверяем выполнение условия оптимальности для каждой незанятой клетки. Полученный снова неоптимальный план, повторяем процесс до тех пор, пока не будет выполняться условие оптимальности, т.е. возвращаемся на 2-й этап.

Через конечное число таких шагов будет найдено оптимальное решение транспортной задачи. Величина разности в незанятой клетке показывает, на сколько уменьшится стоимость плана перевозок, если единицу груза перераспределить в эту клетку.

Новый план представлен в таблице 6.7.

Полученный опорный план удовлетворяет условиям оптимальности.

Значение функции

(ед. ст.).

Таблица 6.7

Матрица планирования		B1	B2	B3	B4	B5	Запасы
Постав-щики	vj ui	v1=7	v2=6	v3=3	v4=7	v5=2
A1	u1=-5	60 2	3	4	80 2	4	140
A2	u2=-2	8	70 4	110 1	14	1	180
A3	u3=0	9	7	10 3	50 7	100 2	160
Потребности		60	70	120	130	100	480

Решим с помощью метода потенциалов станковую задачу.

На предприятии имеется четыре группы станков, каждый из которых может выполнять 5 видов элементарных операций по обработке детали, причём операции могут производиться в любом порядке. Максимальное время работы каждой из групп станков соответственно равно 320, 400, 240 и 400 ч; каждая операция должна выполняться в течение 336, 224, 224, 288 и 288 ч.

Необходимо определить, сколько времени и на какой операции нужно использовать каждую группу станков, чтобы обработать максимальное количество деталей, если производительность каждого станка группы известна и равна .

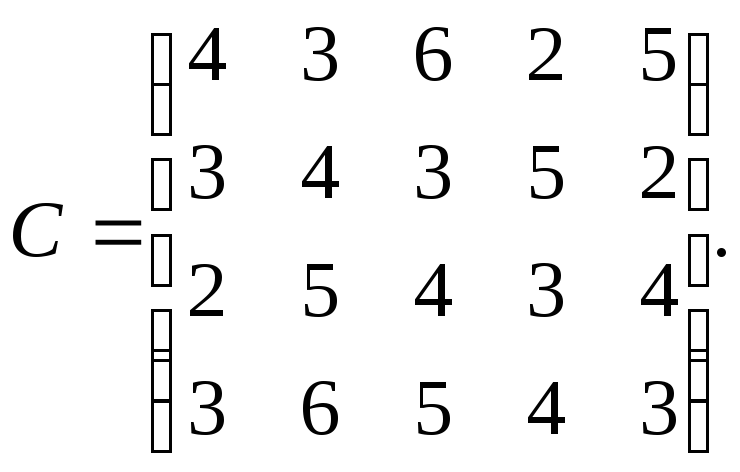
Решение.

Чтобы превратить задачу на минимум, все берем со знаком "-", составим первоначальный опорный план по наименьшим затратам (см. табл 6.8).

(единиц). Осуществим перераспределение поставок по циклу, состоящему из клеток (1,1), (1,5), (3,1), (3,5). Получаем новый опорный план закрепления операций за станками. Он является оптимальным (табл 6.9 на след.с.).

Таблица 6.8

Матрица		Потребители
планирования		B1	B2	B3	B4	B5	Запасы
Постав-щики	vj ui	v1=0	v2=-3	v3=-3	v4=-2	v5=-2	ai
A1	u1=-3	 + -4	-3	224 -6	-2	96 _ -5	320
A2	u2=-3	112 -3	-4	-3	288 -5	-2	400
A3	u3=-2	48 _ -2	-5	-4	-3	192 + -4	240
A4	u4=-3	176 -3	224 -6	-5	-4	-3	400
bj		336	224	224	288	288	1360

Таким образом, для того, чтобы обработать максимальное количество деталей, необходимо, чтобы первая группа станков выполняла первую операцию – 48 ч, третью операцию – 224 ч, пятую операцию – 48 ч, а вторая группа выполняла первую операцию – 112 ч, четвертую – 288 ч. и т. д. При этом будут обработаны: на первой операции – 1056 деталей , на второй операции – 1344 деталей, на третьей операции – 1344 деталей, на четвертой – 1440 деталей, на пятой – 1200 деталей, т.е. полностью можно обработать 1056 деталей.

Таблица 6.9

Матрица		Потребители
планирования		B1	B2	B3	B4	B5	Запасы
Постав-щики	vj ui	v1=0	v2=-3	v3=-2	v4=-2	v5=-1	ai
A1	u1=-4	48 -4	-3	224 -6	-2	48 -5	320
A2	u2=-3	112 -3	-4	-3	288 -5	-2	400
A3	u3=-3	-2	-5	-4	-3	240 -4	240
A4	u4=-3	176 -3	224 -6	-5	-4	-3	400
bj		336	224	224	288	288	1360

Рассмотрим станковую задачу в другом виде.

Условия задачи.

На пяти токарных станках различных типов можно выполнить пять операций по обработке деталей. При этом за каждым из станков может быть закреплена лишь одна операция и одна и та же операция может выполняться только одним станком. Зная время выполнения каждой из операций на каждом из станков, которая задаётся матрицей, составить такое распределение выполняемых операций между станками, при котором суммарные затраты времени на обработку детали являются минимальными.

.

Эта задача аналогична задаче выбора (о назначениях).

Решение

Составим математическую модель задачи. Обозначим через переменную, значение которой равно, если на-м станке-я операция выполняется, и равно0 в противном случае. Тогда закрепление за каждым станком только одной операции выражается равенствами:

а закрепление каждой из операций только на одном станке – равенствами:

Требуется найти такие значения неизвестных , удовлетворяющие системам линейных уравнений и равные0 или 1, при которых функция

F=2х₁₁+4х₁₂+6х₁₃+8х₁₄+3х₁₅+х₂₁+3х₂₂+2х₂₃+7х₂₄+6х₂₅+7х₃₁+2х₃₂+ +4х₃₃+5х₃₄+8х₃₅+9х₄₁+х₄₂+3х₄₃+4х₄₄+6х₄₅+3х₅₁+2х₅₂+х₅₃+4х₅₄+5х₅₅

принимает минимальное значение. Первоначальный опорный план получим методом двойного предпочтения:

Таблица 6.10

Станки		Операции					За каждым станком закреплена
		1	2	3	4	5	одна
	Ui Vj	v1=2	v2=3	v3=3	v4=6	v5=3	операция
I	u1=0	0 V 2	4	6	8	1 v 3	1
II	u2=-1	1 V V 1	3	0 2	7	6	1
III	u3=-1	7	0 V 2	4	1 5	8	1
IV	u4=-2	9	1 V V 1	3	0 4	6	1
V	u5=-2	3	2	1 V V 1	0 v 4	5	1
Каждая операция выполняется только на одном станке		1	1	1	1	1	5

Для построения системы потенциалов должно быть 9 занятых клеток. У нас 5 единиц, введём в базис 4 нулевых клетки по возможности в клетки с наименьшей стоимостью.

Полученный опорный план оптимален.

S==11.

Оптимальным планом является план, согласно которому на первом станке выполняется пятая операция, на втором станке выполняется первая операция, на третьем станке – четвёртая, на четвёртом станке – вторая, на пятом станке – третья операция. Можно заметить, что клетка (4,4) имеет нулевую оценку, т.е. если перераспределить третий станок за второй операцией, а четвёртый за четвёртой операцией, то значение S=11 не изменится, т.е. такой план также оптимален.

Определение оптимального плана транспортных задач, имеющих

некоторые усложнения в их постановке

При нахождении решения ряда конкретных транспортных задач часто бывает необходимо учитывать дополнительные ограничения, которые не встречались выше при рассмотрении простых вариантов данных задач. Остановимся подробнее на некоторых возможных усложнений в постановке транспортных задач.

1. При некоторых реальных условиях перевозки груза из определённого пункта отправления в пункт назначенияне могут быть осуществлены (запрещены перевозки или блокирование соответствующих клеток таблицы данных задачи). Для определения оптимальных планов таких задач предлагают, что тариф перевозки единицы груза из пунктав пунктявляется сколь угодно большой величиной, и при этом условии известными методами находят решение новой транспортной задачи. При таком предположении исключается возможность при оптимальном плане транспортной задачи перевозить груз изв.

2. В отдельных транспортных задачах дополнительным условием является обеспечение перевозки по соответствующим маршрутам определенного количества груза. Пусть, например, из пункта отправления в пункт назначениятребуется обязательно перевестиединиц груза. Тогда в клетку таблицы данных транспортной задачи, находящуюся на пересечении строкии столбца , записывают указанное число и в дальнейшем эту клетку считают свободной со сколь угодно большим тарифом перевозок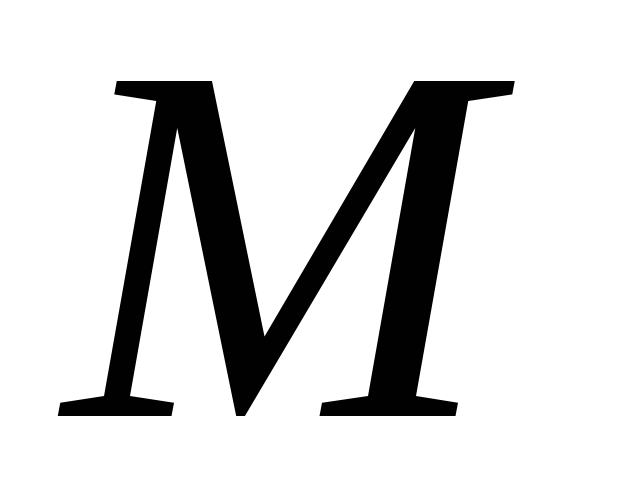. Для получения, таким образом новой транспортной задачи находят оптимальный план (запасы и потребности делаются меньше на).

3. В некоторых транспортных задачах требуется найти оптимальный план перевозок при условии, что из пункта отправления в пункт назначенияперевозится не больше чемединиц груза, т.е.

Сформулированную задачу можно решить так. В таблице исходных данных задачи для каждого -го ограничения предусматривают дополнительный столбец, т.е. вводят дополнительный пункт назначения. В данном столбце записывают те же тарифы, что и в столбце, за исключением тарифа, находящегося в-й строке. Здесь тариф равен. При этом потребностисчитают равными, а потребности вновь введенного пункта назначения полагают равными. Решается полученная транспортная задача методом потенциалов, и будет найден оптимальный план или установлена неразрешимость исходной задачи.