Пример решения станковой задачи

Группа оборудования	Количество единиц оборудования в груп- пе	Производительность единицы оборудования		Первый вариант решения (на каждой группе изготавливают одинаковое количество изделий)		Оптимальный вариант решения (количество изделий, изготавливаемых по группам оборудования)		Оптимальный вариант решения (количество единиц оборудования, занятых изготовлением изделий)
		1-е изделие	2-е изделие	1-е изделие	2-е изделие	1-е изделие	2-е изделие	1-е изделие	2-е изделие	Итого
I	3	10	20	20	20	26	6	8/3	1/3	3
II	3	20	30	36 (x=1,8)	36 (y=1,2)	60	—	3	—	3
III	1	30	80	21 (x=8/11)	21 (y=3/11)	—	80	—	1	1
Всего:				77	77	86	86	—	—	—

Пусть имеются три группы однородного оборудования, на котором необходимо обрабатывать два изделия (две детали). Количество единиц оборудования в каждой группе и производительность при изготовлении изделий каждой группы приведены в таблице 4.1.

Требуется определить, какое количество изделий каждого вида нужно обрабатывать на каждой группе оборудования или какое количество единиц оборудования каждой группы нужно выделить, чтобы изготовить максимальное количество изделий. Для упрощения в этом примере принято, что нужно изготовлять равное количество изделий каждого вида.

Первое заключение, невольно напрашивающееся, заключается в том, чтобы на каждой группе оборудования производилось одинаковое количество изделий того и другого вида, которое и приведено в таблице. Расчёт такого количества ведётся путем решения простейшей системы линейных уравнений. Так, для первой группы оборудования составляется система линейных уравнений:

.

Здесь х – количество станков первой группы оборудования, закреплённых за изделием 1, а у – за изделием 2.

Первое уравнение показывает, что нужно изготовить одинаковое количество изделий первого и второго видов, а второе – что число единиц этой группы оборудования, используемое для изготовления всех изделий, равно трём.

Решение этой системы линейных уравнений даёт х=2, а у=1, т.е. за первым изделием нужно закрепить 2 единицы, а за вторым – одну единицу оборудования первой группы. Суммарная производительность оборудования этой группы, соответствующая данному закреплению, и показана в таблице 1 в столбцах первого варианта решения.

Вычислим отношение производительностей по второму и первому изделиям для каждой группы оборудования и расположим их в порядке убывания (или возрастания) – 8/3(III), 2(I) и 3/2(II). Для группы, у которой это отношение имеет наибольшую величину, все единицы оборудования закрепим за вторым изделием, а у которой это отношение наименьшее – за первым. В оставшейся группе оборудование распределяется так, чтобы выровнять суммарное производство по изделию каждого вида. В данном примере это означает, что III группа оборудования, у которой отношение производительностей максимальное (8/3), нужно целиком закрепить за вторым изделием, а II группу наименьшим отношением производительностей – за первым изделием. Группа I распределяется так, чтобы выровнять объём производства по обоим изделиям.

Для данного примера это выравнивание происходит путём решения системы двух линейных уравнений с двумя неизвестными.

Первое уравнение составляют так, чтобы количество первого и второго изделий, изготовляемое на всех группах оборудования, было одинаковым. В данном случае получим

10х+60=20у+80,

где х и у - количество единиц оборудования I группы, закреплённое соответственно за первым и вторым изделиями.

Второе уравнение составляется исходя из условия, что суммарное количество единиц оборудования I группы, закреплённое за первым и вторым изделиями, не должно превышать имеющегося количества, т.е. для данного случая х+у=3.

Найденное оптимальное решение позволяет увеличить выпуск изделий до 86, что по сравнению с первым возможным вариантом дает увеличение на 11,7% без каких-либо дополнительных затрат. Одновременно это приведёт и к снижению себестоимости изготовляемых изделий.

Для задач большего объёма (с большим числом групп оборудования и видов изделий) найти решение значительно труднее и возможно лишь с использованием методов линейного программирования.

Запишем задачу в следующем виде:

максимизировать целевую функцию

L=10x₁₁+20x₂₁+30x₃₁→max

при условиях

где x_ij – количество единиц оборудования i-й группы, занятое изготовлением изделий j-го вида;

Если количество изделий каждого вида будет задано (что чаще практически и имеет место), то станковая задача может быть поставлена в другом виде. Вместо максимизации количества выпускаемых изделий в этом случае нужно найти минимум времени на производство всех изделий, т.е. минимум целевой функции

где х_ij – время, затрачиваемое i-й группой оборудования на изготовление изделий j-го вида;

а_ij – суммарная производительность всех единиц оборудования i-й группы в единицу времени при изготовлении изделий j-го вида;

N_j – заданное количество изделий j-го вида, которое требуется изготовить.

Так, если для рассматриваемого примера будет задано, что N₁=N₂=50, то задача запишется так:

минимизировать L=x₁₁+x₁₂

при условиях:

В такой задаче вместо групп оборудования могут быть взяты отдельные участки, цехи и предприятия в целом, если они выпускают одни и те же изделия. В этом случае задача ничем не будет отличаться от изложенной выше.

Для постановки и решения станковой задачи необходимо знать производительности или нормы времени на изготовление изделий по каждой группе оборудования, т.е. иметь нормы времени для всех технологических процессов, по которым будут изготавливаться эти изделия. На практике же это бывает очень редко.

Эта задача в несколько изменённом виде используется также при распределении производственной программы между предприятиями, точнее, при решении задач по размещению и концентрации производства.

Задача оптимального раскроя материала (задача по раскрою) является одним из частных случаев задачи по оптимальному использованию комплексного сырья.

Математическая модель задачи использования сырья можно представить в следующем виде.

Пусть выпускается n видов продукции, используется m видов сырья. Обозначим через S_i (i=1,…,m) виды сырья; b_i – запасы сырья i-го вида; P_j (j=1,…,n) – виды продукции; a_ij – количество единиц i-го сырья, идущего на изготовление единицы j-й продукции; с_i – величину прибыли, получаемой при реализации единицы j-й продукции.

Условия задачи запишем в таблице 4.2.

Таблица 4.2

Виды	Запасы	Количество единиц i-го сырья, идущего на изготовление единицы j-й продукции
сырья	сырья	P1	P2	...	Pn
S1	b1	a11	a12	...	a1n
S2	b2	a21	a22	...	a2n
...	...	...	...	...	...
Sm	bm	am1	am2	...	amn
Прибыль		с1	с2	...	сn

Пусть x_ij – количество единиц j-й продукции, которое необходимо произвести. Сама модель:

Найти максимальное значение линейной функции

Z=c₁x₁+ +c₂x₂+…+c_nx_n

при ограничениях

где a_ij - количество сырья, расходуемое на изготовление единицы продукции, b_i – общее количество сырья i-го вида, c_j – величина прибыли, получаемой с единицы j-й продукции.

Система ограничений и функция цели составляют математическую модель рассматриваемой экономической задачи.

Как мы уже выясняли, допустимым решением (или планом) задачи линейного программирования является совокупность чисел х=(х₁,х₂,…,х_n), удовлетворяющих ограничениям задачи. План х^*=(х₁^*,х₂^*,…,х_n^*), при котором целевая функция задачи принимает своё максимальное (минимальное) значение, называется оптимальным.

Форма записи задачи линейного программирования может быть различной. Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения целевой функции при выполнении условий в виде системы неравенств и неотрицательности переменных. Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении минимального значения целевой функции при выполнении условий в виде системы линейных уравнений и неотрицательности переменных. В общей задаче линейного программирования могут быть условия как в виде системы неравенств, так и в виде равенств, причем не на все переменные может быть наложено условие неотрицательности:

.

Указанные выше три формы записи задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Для этого необходимо уметь, во-первых, сводить задачу минимизации функции к задаче максимизации, во-вторых, переходить от ограничений – неравенств к ограничениям – равенствам и наоборот, в-третьих, заменять переменные, которые не подчинены условию неотрицательности.

В том случае, когда требуется найти функцию L=c₁x₁+c₂x₂+…+c_nx_n, можно перейти к нахождению максимума функции L₁= -L= -c₁x₁-c₂x₂-…-c_nx_n, поскольку min L₁= -max(-L).

Ограничение – неравенство исходной задачи линейного программирования, имеющее вид "≤", преобразовать в ограничение – равенство можно добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида "≥" – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство

a_i1x₁+a_i2x₂+…+a_inx_n≤b_i

преобразуется в ограничение-равенство

a_i1x₁+a_i2x₂+…+a_inx_n+x_n+1=b_i (x_n+1≥0),

а ограничение-неравенство

a_i1x₁+a_i2x₂+…+a_inx_n≥b_i

• в ограничение-равенство

a_i1x₁+a_i2x₂+…+a_inx_n-x_n+1=b_i (x_n+1≥0).

В то же время каждое уравнение системы ограничений может быть представлено так:

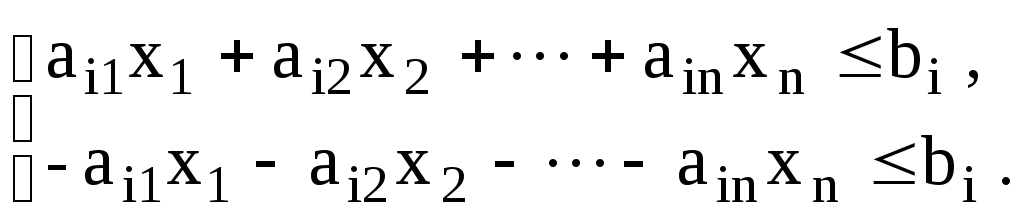
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определённый экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объёму неиспользованного соответствующего ресурса.

Отметим, наконец, что если переменная х_k не подчинена условию неотрицательности, то её следует заменить двумя неотрицательными переменными u_k и v_k, приняв x_k=u_k-v_k.

Рассмотрим каноническую задачу линейного программирования. Перепишем её в векторной форме:

Найти минимум функции L=CX при условиях

A₁x₁+A₂x₂+…+A_nx_n=B, (*)

где C=(с₁;с₂;…;с_n), X=(х₁;х₂;…;х_n); CX – скалярное произведение векторов; А₁,…,А_n и В – m-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членов системы уравнений задачи:

.

Определение. План X=(х₁;х₂;…х_n) называется опорным планом канонической задачи линейного программирования, если система векторов A_ij, входящих в разложение (*) с положительными коэффициентами, линейно независима.

Так как векторы A_ij являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше, чем m.

Опорный план называется невырожденным, если он содержит ровно m положительных компонент, в противном случае он называется вырожденным.

Свойства канонической задачи линейного программирования тесным образом связаны со свойствами выпуклых множеств.

Теорема. Множество планов канонической задачи линейного программирования является выпуклым (если оно не пусто). Непустое множество планов канонической задачи линейного программирования называется многогранником решений, а всякая угловая точка многогранника решений – вершиной.

Теорема. Если каноническая задача линейного программирования имеет оптимальный план, то максимальное (минимальное) значение целевая функция задачи принимает в одной из вершин многогранника решений. Если максимальное (минимальное) значение целевая функция задачи принимает более чем в одной вершине, то она принимает его во всякой точке, являющейся выпуклой линейной комбинацией его вершин.

Теорема. Если система векторов А₁,А₂,…,А_k (k≤n) в разложении (*) линейно независима и такова, что А₁х₁+А₂х₂+…+А_kx_k=B, где все x_j≥0, то точка X=(х₁;х₂;…;х_k;0;…;0) является вершиной многогранника решений (эту теорему мы уже рассматривали).

Теорема. Если X=(х₁;х₂;…х_n) – вершина многогранника решений, то вектора A_ij,соответствующие положительным x_j в разложении (*), линейно независимы.

Сформулированные теоремы позволяют сделать следующие выводы.

Непустое множество планов канонической задачи линейного программирования образуют выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план. В одной из вершин многогранника решений (т.е. для одного из опорных планов) значение целевой функции является максимальным (минимальным) (при условии, что функция ограничена сверху (снизу) на множестве планов). Если экстремальное значение функции принимает значение более чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин.

Вершину многогранника решений, в которой целевая функция принимает экстремальное значение, найти сравнительно просто, если задача, записанная в форме стандартной, содержит не более 2-х переменных или задача, записанная в форме канонической, содержит не более 2-х свободных переменных, т.е. n-r≤2, где n – число переменных, r – ранг матрицы, составленной из коэффициентов в системе ограничений задачи.

Найдем решение задачи (записанной в форме стандартной), состоящей в определении максимального значения функции L=c₁x₁+c₂x₂

при условиях

a_i1x₁+ +a_i2x₂≤b_i (i=1,…,k),

x_j≥0 (j=1,2).

7

8

9

107

Каждое из неравенств системы ограничений задачи геометрически определяет полуплоскость с граничными прямыми a_i1x₁+a_i2x₂=b_i (i=1,…,k), х₁=0 и х₂=0. В том случае, если система неравенств совместна, область её решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей – выпуклое, то областью допустимых решений задачи является выпуклое множество, которое называется многоугольником решений (многогранником, когда n≥3). Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.

Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция L принимает максимальное значение (для стандартной задачи линейного программирования). Эта точка существует тогда, когда многоугольник решений не пуст и на нём целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня с₁х₁+с₂х₂=h (где h – некоторая постоянная), проходящую через многоугольник решений, и будем передвигать её в направлении вектора =(с₁;с₂) до тех пор, пока она не пройдёт через последнюю её общую точку с многоугольником решений. Координаты указанной точки и определят оптимальный план данной задачи.

Заканчивая рассмотрение геометрической интерпретации задачи линейного программирования, отметим, что при нахождении её решения могут встретиться случаи, изображённые на рис. 7-10 (см. на с. 49). Рис. 7 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке A.

Из рис. 8 видно, что максимальное значение целевая функция принимает в любой точке отрезка AB. На рис. 9 изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений, а на рис. 10 – случай, когда система ограничений задачи несовместна. Последние 3 случая – это особые случаи.

Отметим, что нахождение минимального значения линейной целевой функции при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня с₁х₁+с₂х₂=h передвигается не в направлении вектора =(с₁;с₂), а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении её минимального значения.

Итак, нахождение решения задачи линейного программирования на основе её геометрической интерпретации включает следующие этапы:

1. Строят прямые, уравнения которых получают в результате замены в ограничениях знаков неравенств на знаки точных равенств.

2. Находят полуплоскости, определяемые каждым из ограничений задачи.

3. Находят многоугольник решений.

4. Строят вектор =(с₁;с₂).

5. Строят прямую с₁х₁+с₂х₂=h, проходящую через многоугольник решений.

6. Передвигают прямую с₁х₁+с₂х₂=h в направлении вектора , в результате чего либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве планов.

7. Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.

Рассмотрим пример.

Для производства двух видов изделий А и В предприятие использует три вида сырья. Норма расхода сырья каждого вида на изготовление единицы продукции данного вида приведено в таблице. В ней же указаны прибыль от реализации одного изделия каждого вида и общее количество сырья данного вида, которое может быть использовано предприятием.

Таблица 4.3

Вид сырья	Нормы расхода сырья (кг) на одно изделие		Общее количество
	A	B	сырья (кг)
I II III	12 4 3	4 4 12	300 120 252
Прибыль от реализации одного изделия (руб.)	30	40

Учитывая, что изделия А и В могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной.

Решение. Предположим, что предприятие изготовит изделий вида А и изделий вида В. Поскольку производство продукции ограничено имеющимся в распоряжении предприятия сырьём каждого вида, и количество изготовляемых изделий не может быть отрицательным, должны выполняться неравенства:

Общая прибыль от реализации изделий вида А и изделий видаВ составит F=30+ 40.

Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение.

Решим сформулированную задачу геометрическим способом. Сначала определим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств и найдём соответствующие прямые:

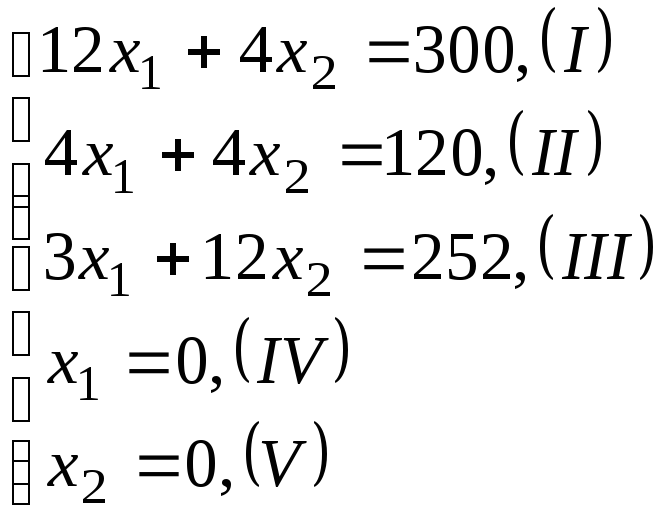
Эти прямые изображены на рис. 11 (см. на с. 53). Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой – нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли её координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае – другая полуплоскость.

Найдем, например, полуплоскость, определяемую неравенством 12+4<300. Для этого, построив прямую 12+4=300 (пр. I), возьмем какую-нибудь точку, принадлежащую одной из полученных полуплоскостей, например, точку O(0;0). Координаты этой точки удовлетворяют неравенству: 12, значит, полуплоскость, которой принадлежит точка O(0;0), определится неравенством 12. Это

и показано стрелками на рис. 11.

Рис. 11 Решение задачи линейного программирования геометрическим способом

Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи.

Как видно из рисунка, многоугольником решений является пятиугольник OABCD. Координаты любой точки, принадлежащей этому пятиугольнику, удовлетворяют данной системе неравенств и условию не отрицательности переменных.

Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику OABCD, в которой функция F принимает максимальное значение. Чтобы найти указанную точку, построим вектор и прямую 30, где h – некоторая постоянная такая, что прямая 30 имеет общие точки с многоугольником решений. Положим, например, h=480 и построим прямую 30 (рис. 11). Точки пересечения с осями .

Если теперь взять какую-нибудь точку, принадлежащую построенной прямой и многоугольнику решений, то её координаты определяют такой план производства изделий А и В, при котором прибыль от их реализации равна 480 руб. Далее, полагая h равным некоторому числу, большему чем 480, мы будем получать различные параллельные прямые. Если они имеют общие точки с многоугольником решений, то эти точки определяют план производства изделий А и В, при которых прибыль от их реализации превзойдет 480 руб.

Перемещая построенную прямую 30в направлении вектора, видим, что последней общей точкой её с многоугольником решений задачи служит точкаВ. Координаты этой точки и определяют план выпуска изделий А и В, при котором прибыль от их реализации является максимальной.

Найдем координаты точки В как точки пересечения прямых II и III. Следовательно, ее координаты удовлетворяют уравнениям этих прямых:

Решив эту систему уравнений, получим =12, =18. Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную = руб.

Вообще, с помощью графического метода может быть решена такая задача линейного программирования, система ограничений которой содержит n неизвестных и m линейно независимых уравнений, если n и m связаны соотношением n-m=2.

Действительно, пусть поставлена каноническая задача линейного программирования: найти минимальное значение линейной функции z= при ограничениях

где все уравнения линейно независимы и выполняется соотношение n-m=2.

Используя метод Гаусса, производим m исключений, в результате которых базисными неизвестными оказались, например, m первых неизвестных , а свободными – два последних: и , т.е. система ограничений приняла вид:

(4.4)

(j=1,2,…,n).

С помощью уравнений преобразованной системы выражаем линейную функцию только через свободные неизвестные и, учитывая, что все базисные переменные - неотрицательные (,j =1,2,…,n), отбрасываем их, переходя к системе ограничений, выраженных в виде неравенств. Таким образом, окончательно получаем следующую задачу:

Найти минимальное значение линейной функции Z= при ограничениях

Преобразованная задача содержит две неизвестных; решая её геометрическим способом, находим оптимальные значения и , а затем, подставляем их в (4.4), находим оптимальные значения .

Пример. Геометрическим способом найти оптимальный план задачи линейного программирования, при котором линейная функция достигает максимального значения при ограничениях

(4.5)

Используя метод Гаусса, произведём три полных исключения . В результате приходим к системе

откуда

(4.6)

Подставляя эти значения в целевую линейную функцию и отбрасывая в системе (4.5) базисные переменные, получаем задачу, выраженную только через свободные неизвестные и :

Найти максимальное значение линейной функции при ограничениях

(подставлены значения из (4.6))

Построим многоугольник решений и линейную функцию в системе координат O (рис. 12). Из рисунка заключаем, что линейная функция принимает максимальное значение в угловой точке В, которая лежит на пересечении прямых 2 и 3. В результате решения системы

находим: ,.

Максимальное значение функции -38+12+84=58. Для отыскания оптимального плана исходной задачи подставляем в (4.6) найденные значения и. Окончательно получим:; ; ;; .

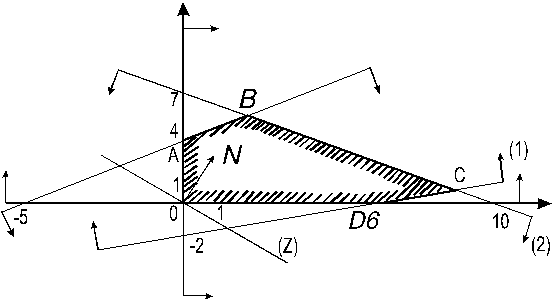
Рис. 12 Решение задачи

Симплекс-метод

Рассмотрим задачу линейного программирования в канонической форме и на минимум целевой функции:

, ,,

(4.7)

где - векторы условий задачи, а В – вектор ограничений этой задачи. Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме.

Допустимое решение задачи (4.7) в канонической форме называется опорным решением (планом) этой задачи, если векторы условий где– номера всех ненулевых координат , образуют линейно независимую систему векторов.

Например, векторы иявляются допустимыми решениями задачи

z=

, 2, 3, 4.

Векторы условий ,образуют, очевидно, линейно независимую систему. Значит,является опорным решением данной задачи. Векторы,,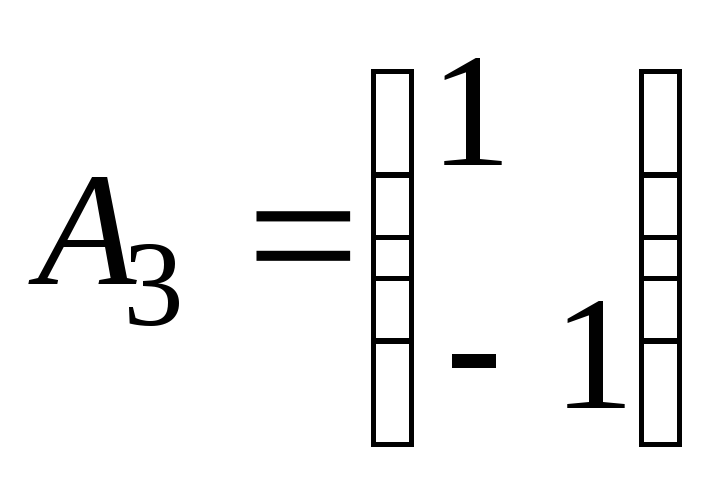линейно зависимы, поэтому₂ не является опорным решением.

Свойства опорных решений

1. Если допустимое множество задачи (4.7) в канонической форме не пусто, то эта задача имеет опорное решение.

2. Опорные решение задачи (4.7) являются крайними точками допустимого множества этой задачи. (Допустимое множество всегда выпукло.)

3. Задача (4.7) в канонической форме имеет лишь конечное число различных опорных решений (либо не имеет их вовсе).

Чтобы найти некоторое опорное решение задачи (4.7), достаточно выбрать базис системы векторов условий этой задачи так, чтобы вектор ограниченийВ раскладывался по нему с неотрицательными коэффициентами.

Если - такой базис итоявляется опорным решением задачи (4.7).

Базис системы векторов условийзадачи (4.7) называетсябазисом опорного решения этой задачи, еслипри.

Пример. Рассмотрим опорное решение задачи

Здесь ибазисы системы. Так как вторая и третья координаты вектораравны 0, тоявляется базисом опорного решения. С другой стороны, четвертая координатаотлична от нуля. Следовательно,не будут базисом.

У любого опорного решения задачи (4.7) не может быть более чем r ненулевых (положительных) координат, где r=rang(). Опорное решение называется невырожденным, если число его ненулевых координат точно равно r и вырожденным – в противном случае.

Любое опорное решение имеет базис, при этом у невырожденного опорного плана базис только один, а вырожденное опорное решение может иметь несколько различных базисов.

Опорные решения играют важную роль при решении задач линейного программирования в канонической форме, так как если задача имеет оптимальное решение, то одно из её опорных решений обязательно будет её оптимальным решением. Таким образом, оптимальное решение задачи линейного программирования в канонической форме можно искать только среди её опорных решений (а их лишь конечное число).

По задаче линейного программирования в канонической форме (4.7) всегда можно составить так называемую симплекс- таблицу:

Таблица 4.4

х1	х2	...	...	хn
a11 a21 . . . am1	a12 a22 . . . am2	... ... ...	... ... ...	a1n a2n . . . amn	b1 b2 . . . bm
- c1	- c2	...	...	- cn	0

Предположим, что - некоторое опорное решение задачи (4.7), а векторыобразуют его базис. Тогда таблицу 4.4 можно преобразовать методом Гаусса в таблицу 4.5.

Таблица 4.5

x1	...	xi1	...	xi2	...	xir	...	xs	...	xn
a'11 a'21 . . . a'k1 . . . a'r1		1 0 . . . 0 . . . 0		0 1 . . . 0 . . . 0		0 0 . . . 0 . . . 1		a'1s a'2s . . . a'ks . . . a'rs		a'1n a'2n . . . a'kn . . . a'rn	di1 di2 . . . dik . . . dir
- c1	...	- ci1	...	- ci2	...	- cir	...	- cs	...	- cn	0

Прибавим к последней строке таблицы 4.5 первую строку, умножив на , вторую строку, умножив на,r - ю строку, умножив на . В результате получим новую таблицу 4.6, гдекоординаты опорного решения, соответствующие векторам базисагдеа(значению целевой функции на опорном решении).

Таблица 4.6, полученная указанным выше способом, называется симплекс-таблицей, приведённой к базису опорного решения, а числаоценками этого базиса.

Таблица 4.6

x1	...	xi1	...	xi2	...	xir	...	xs	...	xn
a'11 a'21 . . . a'r1		1 0 . . . 0		0 1 . . . 0		0 0 . . . 1		a'1s a'2s . . . a'rs		a'1n a'2n . . . a'rn	di1 di2 . . . dir
1	...	i1	...	i2	...	ir	...	s	...	n	0

Имеют место следующие утверждения (рассматривается случай задачи минимизации):

1. Если все оценки некоторого базиса опорного решения не положительны, то оно является оптимальным решением задачи линейного программирования в канонической форме (Признак оптимальности).

2. Для оптимального опорного решения задачи линейного программирования в канонической форме всегда существует базис, все оценки которого неположительны.

3. Предположим, что симплекс-таблица для задачи линейного программирования в канонической форме приведена к базису некоторого опорного решения. Если среди оценок этого базиса имеется положительная оценка , а все остальные элементыs-го столбца таблицы неположительны, то целевая функция не ограничена снизу на допустимом множестве. (Условие неограниченности нулевой функции (особый случай)).

Пример. Рассмотрим опорное решение =(1;0;0;0) задачи:

j = 1,2,3,4.

Приведем симплекс-таблицу для этой задачи к базису опорного решения.

Таблица 4.7

x1	x2	x3	x4			x1	x2	x3	x4			x1	x2	x3	x4			x1	x2	x3	x4
1	1	3	0	1		1	1	3	0	1		1	0	1	1	1		1	0	1	1	1
1	-1	-1	2	1		0	-2	-4	2	0		0	1	2	-1	0		0	1	2	-1	0
10	-1	9	-6	0		10	-1	9	-6	0		10	-1	9	-6	0		0	0	1	-17	-10

Среди оценок базиса есть положительная оценка. Значит, утверждать на этом этапе, что– опорное решение, мы не можем.

С другой стороны, возьмем базис того же опорного решения. Приведя симплекс-таблицу к этому базису (таблица 4.8), получим, что все оценки базисанеположительны. Следовательно,оптимальное решение данной задачи.

Таблица 4.8

x1	x2	x3	x4
1	-1/2	0	3/2	1
0	1/2	1	1/2	0
0	-1/2	0	32/2	-10

Решение задач линейного программирования симплекс-методом

Если известно некоторое опорное решение задачи линейного программирования в канонической форме, то её можно решать симплекс-методом. Симплекс-метод – это направленный перебор опорных решений, при котором значение целевой функции на каждом последующем опорном решение меньше, чем на предыдущем (для задачи минимизации).

Для решения симплекс-методом задачи линейного программирования в канонической форме необходимо выполнить ряд последовательных шагов. На каждом шаге либо возникает базис нового опорного решения, причём на новом опорном плане значение целевой функции обязательно меньше, чем на предыдущем (для задачи минимизации), либо меняется базис исходного опорного решения.

Если на очередном шаге удается установить оптимальность опорного решения или неограниченность целевой функции на допустимом множестве, то следующий шаг не выполняется.

Предположим, что перед выполнением очередного шага симплекс-таблица для задачи (4.7) приведена к базису

(4.8)

некоторого опорного решения . Можно считать, что среди оценок этого базиса есть положительные оценки (в противном случае- оптимальное решение). Выберем любую из положительных оценок, например,В симплекс-таблице, приведённой к базису (4.8), рассмотрим элементы

(4.9)

s-го столбца и соответствующие свободные члены

(4.10)

Можно считать, что среди элементов (4.9) есть положительные элементы (в противном случае целевая функция не ограничена снизу на допустимом множестве). В этом случае необходимо рассматривать все отношения вида

, где ,

(4.11)

т. е. отношение свободного члена к соответствующему элементу s-го столбца (4.9) при условии, что последний положителен. Среди отношений (4.11) выбираем наименьшее.

Если , то симплекс-таблицу приводим к новому базису

(4.12)

т.е. из базиса (4.8) исключаем вектор а вместо него вводим векторЕсли(так заведомо случится, если исходное опорное решение не вырождено), то базис (4.12) является базисом нового опорного решениятакого, что. Если же, то (4.12) является новым базисом исходного опорного решения.

Конечность симплекс-метода

Если задача линейного программирования в канонической форме не имеет вырожденных опорных решений, то через конечное число шагов симплекс-метода она будет решена.

При решении задачи, у которой есть вырожденные опорные решения, может случиться, что, перебирая базисы одного и того же опорного решения, через несколько шагов мы вернёмся к исходному базису, т. е. произойдет зацикливание.

Для предотвращения зацикливания необходимо уточнить правило перехода к новому базису. Это сделать можно, например, следующим образом. Среди оценок базиса (4.8) выбираем положительную оценку с наименьшим номером. Если - такая оценка, а наименьшее из отношений (4.11) определено неоднозначно, то берем наименьшее отношениес наименьшим номеромk.

Пример на применение симплекс-метода

Для изготовления продукции используют 3 вида сырья. При этом можно применять любой из четырех способов производства. Запасы сырья, расход и количество производимой продукции за 1 час работы по каждому способу приведены в таблице 4.9.

Таблица 4.9

Способ произ- водства Сырьё	1	2	3	4	Запас сырья
1	1	2	1	0	18
2	1	1	2	1	30
3	1	3	3	2	40
Выпуск продукции	12	7	18	10

Требуется найти план производства, при котором будет выпущено наибольшее количество продукции. Обозначим через время использованияj-го способа производства (j= 1,2,3,4), получим задачу линейного программирования:

.

Эту задачу сведём к канонической задаче минимизации:

Cоставим симплекс-таблицу. Симплекс-таблица оказывается приведённой к базису опорного решения.

Таблица 4.10

x1	x2	x3	x4	x5	x6	x7
1	x	1	0	1	0	0	18
1	1	2	1	0	1	0	30
1	3	3	2	0	0	1	40
12	7	18	10	0	0	0	0

Выбираем положительную и составляем следующие отношения: Так как наименьшее среди них то необходимо перейти к базисуДля этого достаточно выполнить жорданово преобразование всей таблицы с ведущим элементом.

Таблица 4.11

x1	x2	x3	x4	x5	x6	x7
1	2	1	0	1	0	0	18
0	-1	1	1	-1	1	0	12
0	1	2	2	-1	0	1	22
0	-17	6	10	-12	0	0	-216

Базис является базисом опорного решения=(18;0;0;0;0;12;22). При этомв то время как. Выбираем оценкуи составляем отношенияНаименьшим среди них являетсяСледовательно, переходим к базисуПолучим таблицу 4.12.

Таблица 4.12

x1	x2	x3	x4	x5	x6	x7
1	2	1	0	1	0	0	18
0	-3/2	0	0	-1/2	1	-1/2	1
0	1/2	1	1	-1/2	0	1/2	11
0	-22	-4	0	-7	0	-5	-326

Все оценки базиса неположительны. Следовательно,оптимальное решение канонической задачи минимизации. Поэтомуоптимальное решение исходной задачи. При этом . Таким образом, для того чтобы выпустить наибольшее количество продукции при имеющихся запасах сырья, необходимо в течение 18 ч использовать первый способ производства и в течение 11 ч – четвертый. В результате будет произведено 326 единиц продукции.

Метод искусственного базиса

для отыскания начального опорного решения

Для того, чтобы решить задачу линейного программирования в канонической форме, необходимо предварительно найти некоторое начальное опорное решение этой задачи. Сделать это можно методом искусственного базиса.

Рассмотрим задачу линейного программирования в канонической форме:

,

(4.13)

.

Без ограничения общности можно считать, что Для отыскания опорного решения задачи (4.13) строим вспомогательную задачу:

,

(4.14)

.

Свойства вспомогательной задачи.

1. Вспомогательная задача (4.14) всегда имеет опорное решение.

2. Вектор является опорным решением задачи (4.14).

Таким образом, принимая вектор за начальное опорное решение, вспомогательную задачу можно решить симплекс-методом. Пустьоптимальное опорное решение задачи (4.14).

Если тоопорное решение исходной задачи (4.13). Если же среди чиселесть положительные, то исходная задача (4.13) имеет пустое допустимое множество.

Таким образом, всегда можно либо найти опорное решение исходной задачи, либо установить ее неразрешимость.

Двойственность в линейном программировании

Понятие двойственности. С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной. Первоначальная задача называется исходной.

Связь исходной и двойственной задач состоит в том, что коэффициенты целевой функции исходной задачи являются свободными членами системы ограничений двойственной задачи, свободные членысистемы ограничений исходной задачи служат коэффициентами функции цели двойственной задачи, а матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи. Решение двойственной задачи может быть получено из решения исходной и наоборот.

В качестве примера рассмотрим задачу использования ресурсов. Пусть предприятие имеет m видов ресурсов в количестве (i=1,2,…,m) единиц, из которых производится n видов изделий. Для производства одной единицы j-й продукции расходуется единицi-го ресурса, а её стоимость составляет единиц. Составить план выпуска продукции, обеспечивающий её максимальный выпуск в стоимостном выражении. Обозначим черезколичество единицj-й продукции. Тогда исходную задачу сформулируем так:

Найти вектор , который удовлетворяет ограничениям

и доставляет максимальное значение линейной функции .

Оценим ресурсы, необходимые для изготовления продукции. За единицу стоимости ресурсов примем единицу стоимости выпускаемой продукции. Обозначим через стоимость единицыi-го ресурса. Тогда стоимость всех затраченных ресурсов, идущих на изготовление единицы j-й продукции, равна . Стоимость затраченных ресурсов не может быть меньше стоимости окончательного продукта (не может появиться из "ничего"), поэтому должно выполнятся неравенствоСтоимость всех имеющихся ресурсов выразится величинойИтак, двойственную задачу можно сформулировать следующим образом:

Найти вектор двойственных оценок , который удовлетворяет ограничениям

и доставляет минимальное значение линейной функции

Рассмотренные исходная и двойственная задачи могут быть экономически интерпретированы следующим образом:

Исходная задача. Сколько и какой продукции необходимо произвести, чтобы при заданных стоимостяхединицы продукции и размерах имеющихся ресурсовмаксимизировать выпуск продукции в стоимостном выражении.

Двойственная задача. Какова должна быть цена единицы каждого из ресурсов, чтобы при заданных количествах ресурсов и величинах стоимости единицы продукцииминимизировать общую стоимость затрат?

Переменные называются двойственными оценками или учетными, неявными ценами. В работах Немчинова, Новожилова, Аганбегяна их называют объективно обусловленными оптимальными оценками (о.о.о.о.). Им посвящено много работ, поскольку их экономический смысл в этих математических моделях очень важен для экономического анализа производственной ситуации. Например, в нашей задаче использования ресурсов эти оценки показывают степень дефицитности ресурсов. Более того, величина данной двойственной оценки показывает, на сколько возрастет максимальное значение целевой функции прямой задачи при увеличении количества сырья соответствующего вида на 1 кг.

В результате решения задачи линейного программирования найдется некий оптимальный план. При подстановки этого решения в задачу обнаружится, что некоторые ресурсы используются полностью, а некоторые останутся неиспользованными. Двойственные оценки соответствующих ресурсов будут положительными и нулевыми. Это будет там, где ресурсы не используются полностью. Причем самое узкое место – наиболее дефицитный ресурс – будет иметь двойственную оценку с наибольшим положительным значением. Знание этого "узкого" места уже может влиять на принятие какого – либо управленческого решения. Эти двойственные оценки имеют еще несколько экономических интерпретаций, например, как средство балансировки между суммарными затратами и результатами.

Многие задачи линейного программирования первоначально ставится в виде исходных или двойственных задач, поэтому имеет смысл говорить о паре двойственных задач линейного программирования.

В зависимости от вида ограничений исходные задачи линейного программирования двойственные задачи могут быть несимметричными и симметричными. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде неравенств, причем в последней переменные могут быть и отрицательными. Для простоты постановку задачи условимся записывать в матричной форме.

Исходная задача. Найти матрицу-столбец , который удовлетворяет ограничениями минимизирует линейную функцию

Двойственная задача. Найти матрицу-строку которая удовлетворяет ограничениями максимизирует линейную функцию

В обеих задачах матрица-строка,матрица-столбец,матрица коэффициентов системы ограничений. Связь между оптимальными планами пары двойственных задач устанавливают следующие теоремы двойственности:

1)(первая теорема двойственности). Если из пары двойственных задач одна обладает оптимальным планом, то и другая имеет решение, причем для экстремальных значений линейных функций выполняется соотношение Если линейная функция одной из задач не ограничена, то другая не имеет решения.

2)(вторая теорема двойственности). План исходной задачи и пландвойственной задачи являются оптимальными планами этих задач тогда и только тогда, когда для любогоj=(1,2,…,n) выполняется равенство . Эти теоремы позволяют при решении одной из двойственных задач находить оптимальный план другой.

Разновидностью двойственных задач линейного программирования являются двойственные симметрические задачи, в которых система ограничений как исходной, так и двойственной задач задается неравенствами, причем на двойственные переменные налагается условие неотрицательности.

Исходная задача. Найти матрицу-столбец которая удовлетворяет системе ограниченийи минимизирует линейную функцию

Двойственная задача. Найти матрицу-строку которая удовлетворяет системе ограниченийи максимизирует линейную функциюf=YB.

Систему неравенств с помощью дополнительных переменных можно преобразовать в систему уравнений, поэтому всякую пару симметричных двойственных задач можно преобразовать в пару несимметричных.

Используя симметричность, можно выбрать задачу, более удобную для решения симплекс-методом. Объём задачи, решаемой с помощью ЭВМ, ограничен числом включаемых строк, поэтому задача, довольно громоздкая в исходной постановке, может быть упрощена в двойственной формулировке. При вычислениях без помощи машин использование двойственности упрощает вычисления.

Виды математических моделей двойственных задач

На основании рассмотренных несимметричных и симметричных двойственных задач можно заключить, что математические модели пары двойственных задач могут иметь один из следующих видов:

Несимметричные задачи.

(4.15) Исходная Двойственная (4.16) Исходная Двойственная

задача задача задача задача

Симметричные задачи.

(4.17) Исходная Двойственная (4.18) Исходная Двойственная

задача задача задача задача

Таким образом, прежде чем записать двойственную задачу для данной исходной, систему ограничений исходной задачи необходимо привести к соответствующему виду.

На примерах рассмотрим алгоритм составления двойственной задачи.

Исходная задача. Найти минимальное значение линейной функции при ограничениях

.

Рассмотренная задача относится к симметричным двойственным задачам на отыскание минимального значения линейной функции. Для того, чтобы можно было записать двойственную задачу, ее модель должна иметь вид (4.17). Переход осуществляется умножением первого неравенства на –1. Исходная задача:

.

Двойственная задача:

.

Матрица коэффициентов ограничений в двойственной задаче является транспонированной матрицей коэффициентов ограничений исходной задачи.

Рассмотрим теперь случай, когда число ограничений не совпадает с числом переменных.

Исходная задача. Найти минимальное значение линейной функции при ограничениях

.

.

Двойственная задача (несимметричная; вид (4.15)). Найти максимальное значение линейной функции при ограничениях