DM_1 / Деталі машин КЛ [Стадник В. А

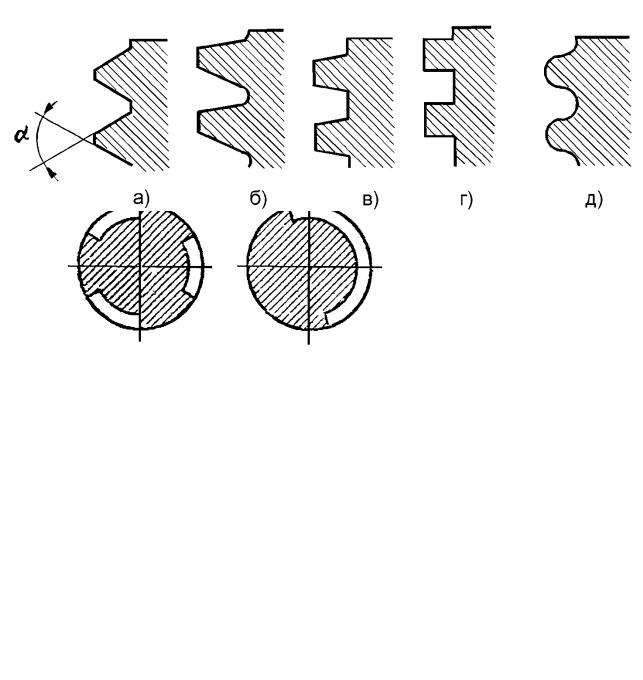
(гвинтової лінії) навкруг бокової поверхні циліндра називається витком. Розрізняють ліву і праву гвинтові лінії (ліву і праву різьби).

Контур перерізу різьби в осьовій площині циліндра (гвинта), називається профілем різьби. Розрізняють п'ять основних типів різьб в залежності від профілю (рис. 15.5): а – трикутна; б – упорна; в – трапецеїдальна і д – кругла. Всі вони знаходять застосування у гвинтових механізмах, при цьому вид профілю вибирають в залежності від умов роботи, призначення механізму, вимог точності і ККД.

Рис. 15.5. Профілі різьби В залежності від числа заходів розрізняють однозаходні і багатозаходні

різьби (рис. 15.6).

Рис. 15.6. До визначення кроку і ходу різьби

340

Багатозаходна різьба утворюється при переміщенні по паралельних гвинтових лініях декількох поряд розташованих профілів (див. рис. 15.6). Число заходів різьби визначають за числом збігаючих витків на торці гвинта.

Геометричні параметри різьби

Всі геометричні параметри, а також їх позначення для більшості різьб і допуски на їх розміри стандартизовані.

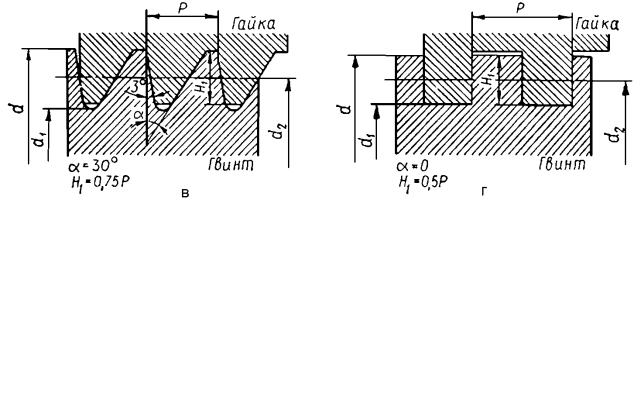
Різьба характеризується такими параметрами (рис. 15.7): зовнішнім d ( D ), внутрішнім d1 ( D1 ) і середнім d2 ( D2 ) діаметрами ( d відноситься до гвинта, D – до гайки); кроком різьби P ; робочою висотою профілю H1 ;

кутом прфілю α ; числом заходів Z ; ходом різьби Ph ; кутом підйому різьби

ψ .

Рис. 15.7. Геометричні параметри різьб для передачі гвинт-гайка: а – трикутна різьба; б – трапецеїдальна різьба;

в – упорна різьба; г – прямокутна різьба Кути профілю різьби стандартизовані: для трикутної різьби α =60˚; для

трапецеїдальної α =30˚ і для упорної α =30˚. (рис. 15.7).

341

Кут підйому різьби ψ дорівнює куту підйому гвинтової лінії на середньому циліндрі різьби.

Згідно з рис. 15.3. із ▲АВС

де Ph - хід різьби, рівний відстані між одноіменними сторонами двох сусідніх витків однієї ж і тієї ж гвинтової поверхні; для одно західних різьб Ph = P , для багатозахідних - Ph = P × Z , де Z - число заходів.

15.2 Силові співвідношення, умови самогальмування і ККД гвинтової

пари

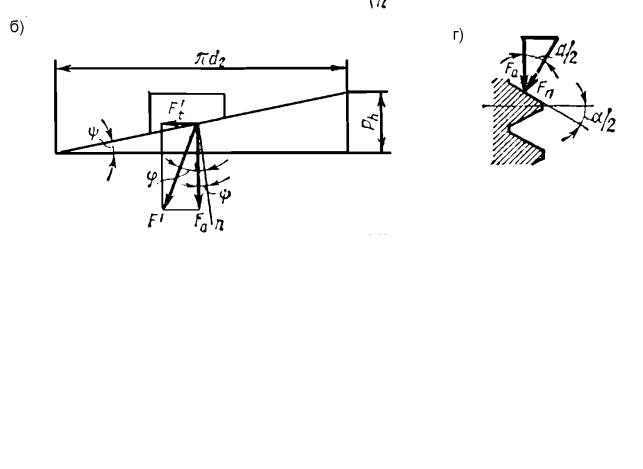
Розглянемо сили, які виникають у гвинтовій парі з прямокутною різьбою (рис. 15.8,а). Розгорнемо виток прямокутної різьби по середньому діаметру

Рис. 15.8. До визначення силових співвідношень у гвинтовій парі

342

d2 в похилу площину, а гайку замінимо повзуном (рис. 15.8. а). Підйому повзуна по похилій площині відповідає нагвинчування гайки на гвинт.

Як відомо із теоретичної механіки, сила взаємодії F між похилою площиною і повзуном, яка виникає при русі його по похилій площині, являє собою рівнодіючу нормальної сили і сили тертя між ними і нахилена до нормалі n поверхні їх дотикання під кутом тертя ϕ .

Розкладемо силу F на дві складові: осьову силу Fa , діючу на гвинтову

відгвинчування гайки або гвинта. В цьому випадку при розкладанні сили

знаходиться в покої, на неї діє осьова сила Fa Розкладемо силу Fa дві складові:

343

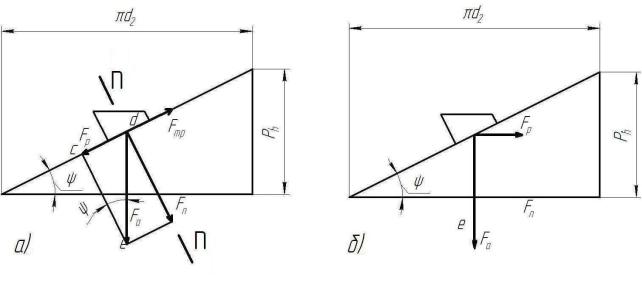
рушійну силу Fp, яка діє в похилій площині , і силу Fn, перпендикулярну до

похилої площини (рис. 15.9, а). Сила по відношенню

Рис. 15.9. До визначення умови самогальмування і ККД передачі: а – умова самогальмування; б – ККД

до гайки (повзуна) направлена в сторону відгвинчування (спуску повзуна з похилої площини), а сила тертя Fтp , яка є результатом дії нормальної сили Fn

запобігає цьому спуску. Щоб гайка не відгвинчувалась без прикладання зовнішнього моменту, необхідно забезпечити умову

Але Fp = Fa × sinψ (з ▲ cde),

а Fтp = Fn × f = Fa × cosψ × f ,

де f - коефіцієнт тертя.

Підставивши значення Fp і Fтp у вираз (15.5), одержимо умову

самогальмування гвинтової пари.

Fa × sinψ £ Fa × cosψ × tgϕ ,

звідки tgψ < tgϕ ,

де ρ - кут тертя (ϕ = arctgf ).

344

За умовою (15.6) перевіряють, наприклад, гвинтові домкрати (див. рис. 15.1). Вантаж не повинен опускатися доти, поки до зубчастого колеса, зв'язаного з гайкою (рукоятки), не прикладена колова сила. Різьби багатозахідні для передачі руху мають кут підйому гвинтової лінії різьби ψ =8˚÷16˚, кут тертя ϕ =2˚÷6˚ ( для сталевого гвинта і бронзової гайки) і ϕ =4˚÷8˚ ( для сталевого

гвинта і чавунної гайки).

Коефіцієнт корисної дії η гвинтової пари з прямокутною різьбою при нагвинчуванні гайки або угвинчуванні гвинта.

При підйомі повзуна по похилій площині рушійною силою Fр (рис. 15.9.

Скориставшись формулами (15.7 і 15.8), одержуємо формулу для визначення ККД

Для випадку самогальмування (ψ < ϕ ) при підйому вантажу ККД менше

0,5.

Приблизні криві зміни ККД гвинтової передачі дані на рис. 15.10: 1 – кочення, при перетворенні обертального руху в поступальний; 2 – те ж саме, поступального руху в обертальний; 3 – ковзання з застосуванням спеціальних мастильних матеріалів; 4 – ковзання для однозахідної різьби.

345

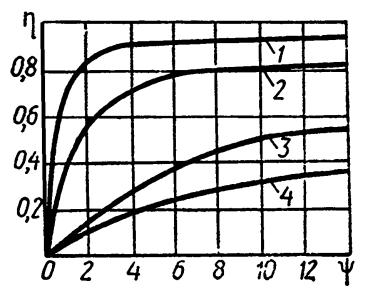
Рис. 15.10. Вплив кута підйому різьби на ККД

При відгвинчуванні гайки або гвинта (відповідає спуску повзуна по похилій площині) рушійною силою буде сила Fa рис. 15.9. б, а силою

корисного опоруFt ′ .

Тоді

Силові співвідношення, умови самогальмування і ККД гвинтової пари з

трикутною або трапецеїдальною різьбою

Так як міркування і висновки для трикутної і трапецеїдальної різьб однакові, то розглянемо їх стосовно до трикутної різьби. Якщо в розглянутій гвинтовій парі замінимо прямокутну різьбу трикутною, то сила тертя в різьбі, а отже, і колова сила гвинтової пари будуть мати інші значення.

Визначимо силу тертя і установимо співвідношення між силами тертя у прямокутній і трикутних різьбах. Для спрощення висновків кут нахилу різьби приймемо рівним нулю. Сила тертя для прямокутної різьби (рис. 15.8, в)

346

Fтp = f × Fa

Із одержаної формули випливає, що у порівнянні з прямокутною різьбою в

Тому по аналогії з прямокутною різьбою випливає, що для трикутної різьби колова сила

умова самогальмування визначається виразом ψ ≤ ϕ′, коефіцієнт корисної дії

347

а для самогальмівної гвинтової пари, де ψ ≤ ϕ′ , η =0,5.

Передатне число. У гвинтових механізмах обертання гвинта або гайки здійснюється звичайно за допомогою маховичка, шестірні, рукоятки і т. д. Передатним числом гвинтового механізму умовно називають відношення переміщення маховичка до переміщення гайки або гвинта за один оберт.

Проведений розрахунок показує, що при простій і компактній конструкції гвинтовий механізм дозволяє одержувати значний виграш у силі.

15.3 Конструкції елементів у передачі гвинт-гайка.

Розрізняють два типи передач гвинт-гайка: передачі з тертям ковзання і передачі з тертям кочення.

Передачі з тертям ковзання мають найбільше розповсюдження завдяки простоті конструкції і виготовлення.

Гвинти передач поділяються на вантажні і ходові. Вантажні призначені для створення великих зусиль (домкрати, преси і т. п.). При реверсному русі під навантаженням застосовують трапецеїдальну різьбу (див. рис. 15.7, б), а при великих односторонніх навантаженнях – упорну (див. рис. 15.7, в). Для одержання самогальмівної гвинтової пари (домкрати) застосовують однозахідну різьбу. Прямокутна різьба (рис. 15.7, г) не стандартизована через нетехнологічність її виготовлення, однак, зважаючи на підвищений ККД (кут профілю α =0˚) таку різьбу інколи використовують у передачах гвинт-гайка.

348

Ходові гвинти призначені для одержання точних переміщень. Для зменшення тертя вони, як правило, мають трапецеїдальну багато західну різьбу. Для точних гвинтів іноді застосовують метричну різьбу (див. рис. 15.7, а).

Конструктивно гвинт являє собою циліндричний стержень суцільної (див. рис. 15.1, а) або збірної конструкції.

Гайки вантажних гвинтів виготовляють суцільними у вигляді втулок з одним опорним фланцем. Якщо гайка нерухома, то від прокручування в корпусі вона утримується шпонками або гвинтами. Гайки, що обертаються, установлюють в корпусі на кулькових упорних або радіально-упорних підшипниках (рис. 15.1. а) і радіальних підшипниках ковзання або кочення, обхвачуючи гайку.

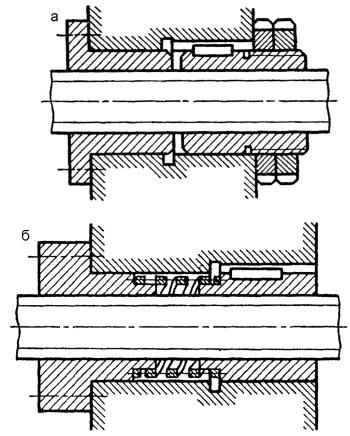
Гайки ходових гвинтів (наприклад, гайка ходового гвинта токарного верстата) виготовляють здвоєними (рис. 15.11, а), щоб усунути зазори, створені при виготовленні і складанні або в результаті спрацювання різьби. Здвоєна

Рис. 15.11. Регулювання зазора: а – з допомогою різьби; б – з допомогою пружини

349