Матрицы

§5. Матрицы

1^о .Основные определения.

Пусть – коммутативное кольцо с единицей.

Определение 1. Матрицей размеров над кольцом называется прямоугольная таблица из элементов кольца и имеющая строк и столбцов:

где – номер строки, – номер столбца, − элементы матрицы, и − порядки матрицы. В этом случае говорят, рассматриваемая матрица размера . Если , то матрица называется квадратной, а число – её порядком.

Далее для изображения матрицы применяются либо круглые скобки, либо сдвоенные прямые:

или .

Для краткого обозначения матрицы используется либо заглавная латинская буква , либо символы , , либо с разъяснением: .

Множество всех матриц размера обозначается .

Частные случаи матриц.

1. Если , то матрица называется квадратной. Её диагональ называется главной диагональю, а – побочной диагональю.

2. Диагональная матрица – это матрица, у которой все ненулевые элементы находятся на главной диагонали, т.е. .

3. Диагональная матрица вида называется скалярной.

4. Скалярная матрица с единичными элементами на главной диагонали называется единичной. Обозначается или , где – ее порядок.

5. Матрица размера , у которой все элементы равны нулю, называется нулевой и обозначается .

6. Если , то матрица называется строкой, или матрица-строка, или строка. Если столбцовая = матрица-столбец = столбец.

Определение 2. Две матрицы называются равными, если эти матрицы имеют одинаковые порядки и их соответствующие элементы совпадают.

2^о. Операции над матрицами и их свойства.

Определение 3. Суммой матриц и (т.е. имеющих одинаковые порядки) называется матрица : .

Обозначение: .

Замечание. Сумма матриц – алгебраическая операция.

Пример.

.

Свойства (сложения матриц).

1) Коммутативность сложения, т.е., справедливо .

2) Ассоциативность сложения, т.е., справедливо .

3) .

4) . При этом, если , то . Матрица называется противоположной к и обозначается .

Доказательство свойств – самостоятельно прямыми вычислениями.

Теорема 1. Множество относительно сложения образует абелеву группу.

Доказательство следует из свойств 1)–4).

Определение 4. Произведением элемента на матрицу называется матрица

Обозначение: .

Операция, сопоставляющая и их произведение называется умножением элемента кольца на матрицу.

Свойства (умножения матрицы на элемент кольца).

выполняется

1) .

2) .

3) .

4) .

Доказательство свойств – самостоятельно прямыми вычислениями.

Замечание. Разность двух прямоугольных матриц и определяется равенством .

Определение 5. Произведением матриц размера и размера называется матрица размеров такая, что каждый элемент .

Обозначение: .

Операция произведения на называется перемножением этих матриц.

Из определения следует, что элемент матрицы , стоящий в –ой строке и –ом столбце, равен сумме произведений элементов –ой строки матрицы на –ый столбец матрицы .

Примеры.

1) ,

2) .

Таким образом, две матрицы можно перемножать, если число столбцов матрицы равно числу строк матрицы . Тогда матрица называется согласованной с . Из согласованности с не следует согласованность с . Если даже условие согласования выполняется, то в общем случае .

Свойства (умножения матриц).

1) Ассоциативность умножения матриц, т.е., справедливо .

Доказательство. Из определения 5 следует, что элемент матрицы равен , а элемент матрицы равен . Равенство следует из возможности изменения порядка суммирования.

2) Дистрибутивность сложения относительно умножения, т.е.,

, .

, .

Доказательство следует из определения суммы и произведения матриц.

3) .

Доказательство. Пусть, и . Тогда . Здесь – символ Кронекера.

.

4) .

5) .

Доказательство свойств 4)-5) проводится аналогично свойству 3).

6) .

Теорема 2. Множество квадратных матриц порядка над кольцом относительно операций сложения матриц и умножения матриц образует кольцо с единицей.

Доказательство. Из теоремы 1 – абелева группа. Так как любые матрицы из согласованы умножение определено. Дистрибутивность и ассоциативность умножения следует из свойств 2) и 1). Свойство 3) демонстрирует наличие единицы.■

Замечание. В общем случае произведение матриц не коммутативно. Например,

.

Но из свойств 4) и 5) умножение квадратной матрицы на и коммутирует. Также коммутирует умножение квадратной матрицы на скалярную.

3^о. Блочные матрицы.

Пусть матрица при помощи горизонтальных и вертикальных прямых разбита на отдельные прямоугольные клетки, каждая из которых является матрицей меньших размеров и называется блоком исходной матрицы. В этом случае рассматривается как некоторая новая, блочная матрица , элементами которой являются блоки указанной матрицы ( – элементы матрицы, поэтому заглавное). Здесь – номер блочной строки, – столбца.

Например, если

, то ,

, , .

Замечательным является факт, что операции с блочными матрицами совершаются по тем же правилам, что и обычными, только в роли элементов выступают блоки. Действительно, если , то , где вычисляется по обычному правилу умножения матрицы на число. Аналогично, если и имеют одинаковые порядки и одинаковым образом разбиты на блоки, то сумме отвечает блочная матрица : .

Для умножения на необходимо согласовать их разбиение на блоки, т.е. число столбцов каждого блока равно числу строк блока . Тогда .

Для доказательства необходимо расписать правую и левую части в терминах обычных элементов матриц . Пусть . Если , то и , откуда следует, что

, что и требовалось доказать.

Пример. Пусть , , т.е.,

, ,

где

,

.

Тогда . Аналогично находятся остальные . В результате получаем

.

В качестве применения блочных матриц рассмотрим

Определение 6. Прямой суммой квадратных матриц порядков соответственно называется квадратная матрица порядка : .

Обозначение: .

Свойства (прямой суммы).

1) .

2) .

3) .

4) .

Доказательство – самостоятельно.

§6. Группа перестановок. Знак перестановки.

1^о. Знак перестановки.

Напомним, что если – множество из -элементов, , то перестановкой степени называется взаимнооднозначное отображение . Обозначение: – множество всех перестановок степени : .

Лемма 1. Число различных перестановок равно

Лемма 2. Множество перестановок образует группу относительно умножения . При этом тождественная перестановка − нейтральный элемент группы, симметричный элемент получается сменой строк. Группа − не коммутативная группа.

Отметим, что если в перестановке поменять местами любые столбцы, то получится та же перестановка.

Углубим проведенное ранее исследование.

Определение 1. Пусть – перестановка степени и пусть . Тогда пара называется инверсией относительно , если .

Перестановка называется четной, если число инверсий относительно четное, и перестановка называется нечетной, если число инверсий − нечетное.

Знак перестановки – это ,где – число инверсий.

Обозначение: .

Таким образом, если – четная, то , и если – нечетная, то .

Пример. . Возможные пары . Их них подчеркнутые – инверсии. Таким образом, , т.е. – четная.

Теорема 1.

1. Знак единичной перестановки равен 1.

2. Если .

3. .

Доказательство.

1. В единичной перестановке инверсий нет; поэтому .

2. Пусть – множество инверсий относительно , а – множество инверсий относительно .

Легко видеть, что если , то . Следовательно, между множествами устанавливается взаимнооднозначное соответствие

.

3. Пусть – множество инверсий относительно ,

– множество инверсий относительно ,

– множество инверсий относительно : .

Тогда надо доказать, что , т.е. – четное число – это надо доказать.

Пусть ,

,

,

.

Введем следующее обозначение: пусть - это множество пар . Тогда справедлива следующая множественная схема:

М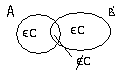ежду множествами существует взаимнооднозначное соответствие : .

Поэтому из картинки видно , т.е. четное число. ▄

Следствие: .

2^о. Транспозиция как пример нечетной перестановки. Разложение перестановки в произведение транспозиций.

Обозначение: Пусть . -перестановкой будем называть перестановку, при которой

Определение 2: Перестановка вида называется транспозицией. Они имеют вид , где точками обозначены элементы, остающиеся на своих местах.

Теорема 2: Транспозиция – нечетная перестановка.

Доказательство: Вычислим число инверсий. Инверсиями являются пары , где , пара , где , и пара . Их всего будет , т.е. нечетное число. ▄

Замечание: Произведение вида означает, что в нижней строке надо поменять местами и .