линейные_пространства

§9. Линейное пространство

1^о. Определение и простейшие свойства

Пусть даны поле с элементами, называемыми скалярами и обозначаемыми малыми греческими буквами , , , … и множество элементов, называемых векторами и обозначаемых латинскими буквами . Введем на алгебраическую операцию сложения, которая каждой паре элементов ставит в соответствие третий элемент , называемый суммой и и обозначаемый , а также операцию умножения скаляра на вектора, которая и ставится в соответствие , называемый произведением вектора на скаляр и обозначаемый

Определение 1. Множество вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем , если удовлетворяются следующие аксиомы:

1) является абелевой группой;

2) Для любых и выполняются равенства:

а) Умножение на не изменяет , т.е. .

б) .

в) Умножение вектора на скаляр дистрибутивно относительно сложения скаляров, т.е. .

г) Умножение вектора на скаляр дистрибутивно относительно сложения векторов, т.е. .

Обозначение. .

Замечание. Так как ­­− абелева группа, то существует единственный нейтральный (нулевой) элемент, обозначаемый , для каждого вектора существует единственный симметричный (противоположенный) элемент, обозначаемый , и для уравнение имеет единственное решение , называемое разностью и .

Свойства линейного пространства.

1) выполняется .

2) выполняется .

3) выполняется .

4) выполняется .

5) .

6) .

7) .

Доказательство.

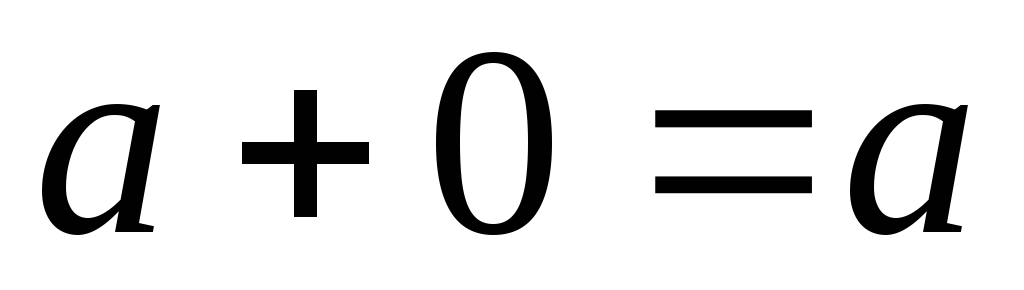
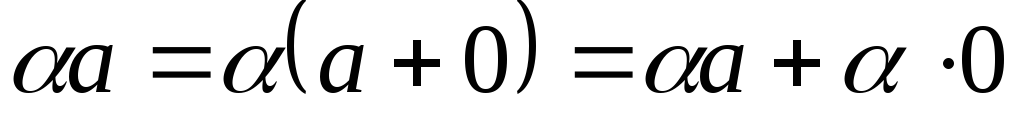
1. Так как в силу г) имеем 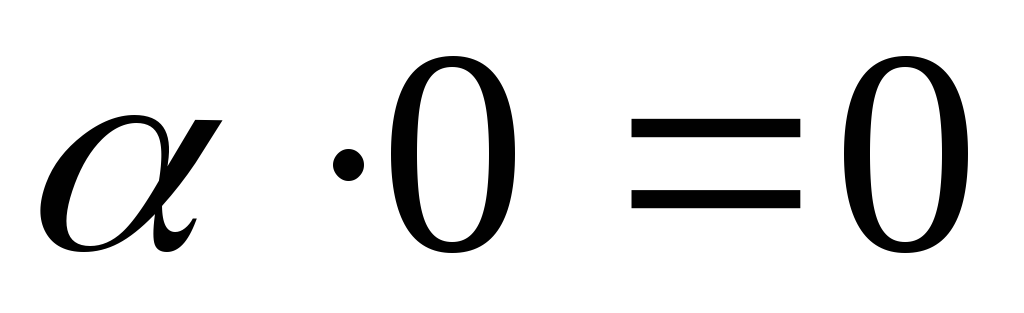. Аналогично, имеем .

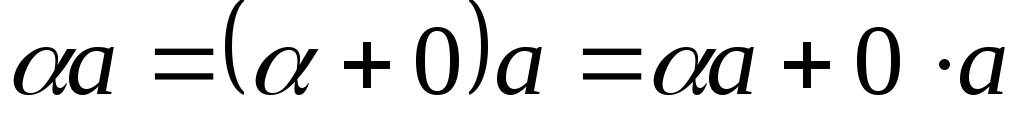
2. В силу г) имеем в силу разности векторов .

3. Следует из 2) при .

4. Доказывается аналогично.

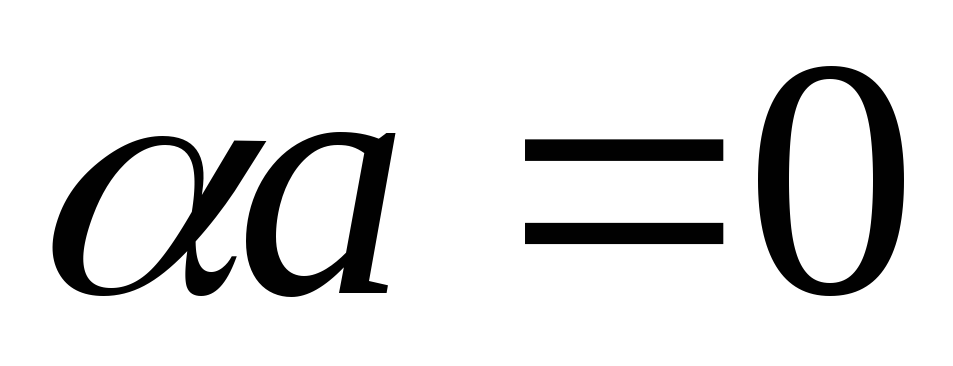5. Если и , то умножая это равенство на получаем: и . Т.о., если , то . Обратное утверждение следует из 1).

6. Из .

7. Аналогично. ■

Примеры.

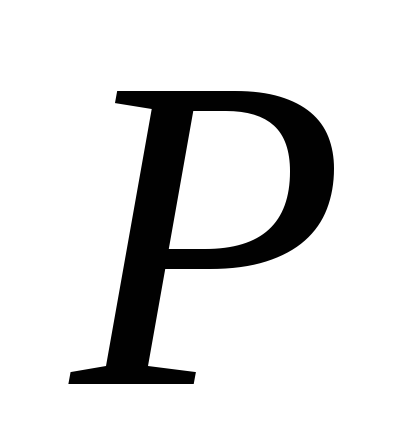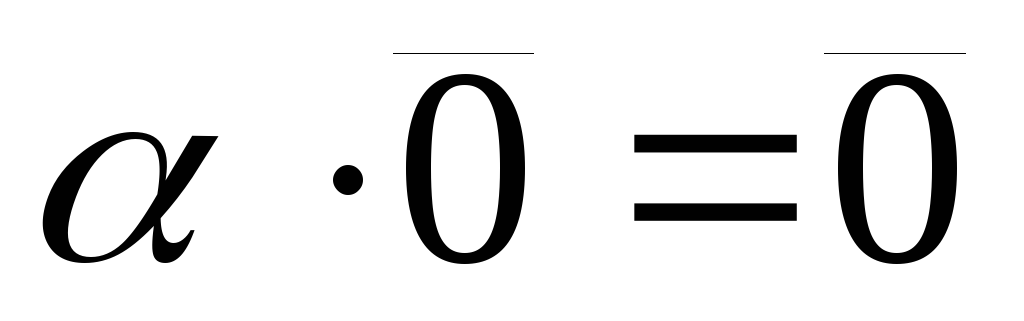
1. Если − поле и , то имеем − векторное пространство, называемое нулевым.

2. − векторное пространство комплексных чисел над полем вещественных чисел. − векторное пространство вещественных чисел над полем рациональных чисел.

3. Множество матриц размера образует векторное пространство .

4. Множество многочленов степени не выше n образует векторное пространство .

5. Множество непрерывных на функций образует векторное пространство .

6. – n-мерное координатное пространство (или арифметическое пространство), элементами которого являются упорядоченные наборы из n чисел: . Операции определены следующим образом:

;

.

Задача. Проверить выполнение аксиом векторного пространства.

2^о. Линейно зависимые и линейно независимые системы векторов

Это понятие является обобщением понятия линейной зависимости строк.

Определение 2. Линейной комбинацией векторов с коэффициентами называется выражение вида: .

Определение 3. Вектора называются линейно независимыми, если , из которых хотя бы одно отлично от нуля, т.е. линейная комбинация с этими является нулевым вектором V, т.е. . Вектора , не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами, называются линейно независимыми, если их линейная комбинация является нулевым элементом V лишь при условии, что

Теорема 1.

1) Для того, чтобы элементы были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов был линейной комбинацией остальных.

2) Если среди один элемент нулевой, то они линейно зависимы.

3) Если часть элементов множества линейно зависима, то и все элементы линейно зависимы.

Доказательство.

1. Аналогично доказательству из §8.

2. Если и – любое, например, линейно зависимы.

3. Если – линейно зависимы, то одновременно неравные нулю, так что и хотя бы одно из отлично от нуля линейно зависимы. ч.т.д.

Пример. Рассмотрим линейное пространства и докажем, что n элементов из вида , ,…, линейно независимы, а добавление еще одного элемента приводит к линейно зависимой системе. Действительно, рассмотрим линейную комбинацию с . Имеем . Вектор справа равен нулю, если все , т.е. – линейно независимы.

Добавим . Тогда по теореме 1, п. 1, достаточно показать, что x – линейная комбинация . Действительно, .

3^о. Базис линейного пространства и координаты вектора в базисе.

Определение 5. Совокупность векторов называют базисом в , если

1. вектора – линейно независимы;

2. для найдутся . (1)

При этом равенство (1) называется разложением элемента по базису , а называются координатами относительно базиса .

Теорема 2 (о единственности разложения по базису). Любой элемент может быть единственным образом разложен по базису , т.е. координаты вектора относительно базиса определяются однозначно.

Доказательство. Пусть и . Тогда . В силу линейной независимости , что и требовалось доказать.

Теорема 3 (операции над векторами, заданными своими координатами). При сложении любых двух векторов и их координаты (относительно любого фиксированного базиса в ) складываются; при умножении на , все координаты вектора умножаются на это число.

Доказательство. Пусть – базис в , , . Тогда в силу аксиом линейного пространства , . В силу единственности разложения по базису что теорема доказана.

Примеры.

1. Базис в – любое ненулевое число.

2. . Базис образуют матрицы 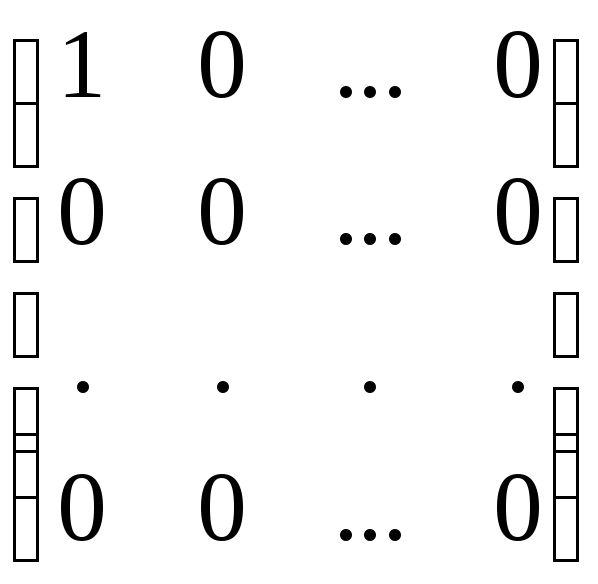, , …, 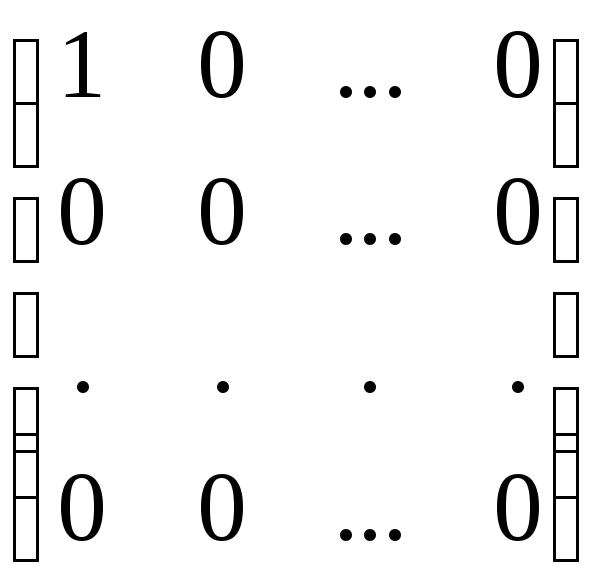с одним единичным элементом.

3. – множество многочленов степени не выше n. Базис: , , …, .

4. – см. выше.

4^о. Размерность линейного пространства.

Определение 6. Линейное пространство называется n–мерным, если

1. В нем n линейно независимых векторов.

2. векторов линейно зависимы.

Тогда n называется размерностью и обозначается .

Определение 7. Линейное пространство называется бесконечномерным, если в нем любое число линейно независимых векторов.

Выясним связь между понятием базиса и размерности линейного пространства.

Теорема 4. Если – линейное пространство размерности n, то линейно независимых векторов этого пространства образуют его базис.

Доказательство. Пусть – система n линейно независимых векторов из . Если – любой вектор из , то по Def 6, вектора – линейно зависимы, т.е.

и среди есть хотя бы одно отличное от нуля. Очевидно, что (т. к. иначе – линейно зависимы)

, т.е.

– линейная комбинация т. к. – произвольный, то –базис.

Теорема  5. Если имеет базис, состоящий из n элементов, то .

Доказательство. Пусть – базис в . Достаточно показать, что векторов линейно зависимы. Разложим их по базису:

,

…

,

где .

Очевидно, что линейная зависимость векторов эквивалентна линейной зависимости строк матрицы

.

Но строки этой матрицы заведомо линейно зависимы, т. к. порядок базисного минора не превосходит n и хотя бы одна из строк не является базисной, и по теореме о базисном миноре представляет собой линейную комбинацию базисных строк (а стало быть и остальных).

Примеры.

1. .

2. .

3. .

4. .

5. .

5^о. Изоморфизм линейных пространств.

Здесь будет показано, что линейные пространства одной и той же размерности в смысле некоторых свойств, связанных с введенными операциями, не отличаются друг от друга.

Определение 6. Два произвольных линейных пространства V и над одним и тем же полем называются изоморфными, если между элементами этих пространств можно установить взаимнооднозначное соответствие так, что если векторам отвечают соответственные вектора , то вектору отвечает вектор , а вектору при отвечает вектор .

Свойства изоморфных пространств.

1. Нулевому элементу V соответствует нулевой элемент и наоборот.

Доказательство: Если .

2. Если элементам соответствуют , то линейная комбинация векторов равна нулю V, т.е. линейная комбинация с теми же коэффициентами равна нулю, т.е. .

Доказательство следует из 1.

3. Если V и изоморфны, то максимальное число линейно независимых векторов в каждом из пространств одно и тоже, т.е. два изоморфных пространства имеют одну и туже размерность.

4. Пространства разных размерностей не могут быть изоморфными.

Теорема 6. Любые два –мерных линейных пространства V и над одним и тем же полем изоморфны.

Доказательство. Выберем в V базис ­­­− базис Каждому элементу , поставим в соответствие элемент с теми же координатами в базисе .

Однако это соответствие взаимнооднозначно, т.к. имеет единственным образом определенные координаты , которые в свою очередь, определяют единственный элемент .