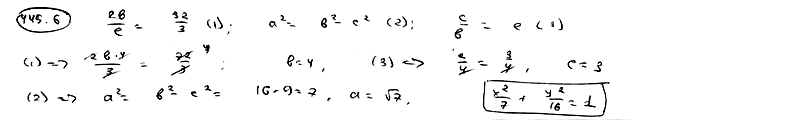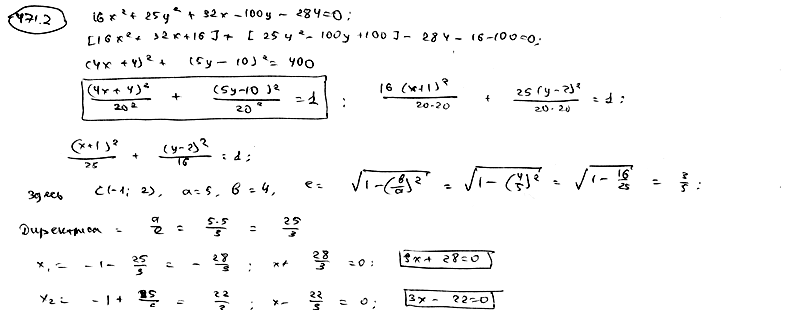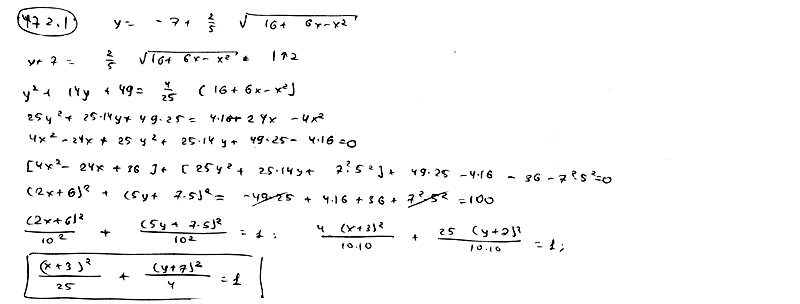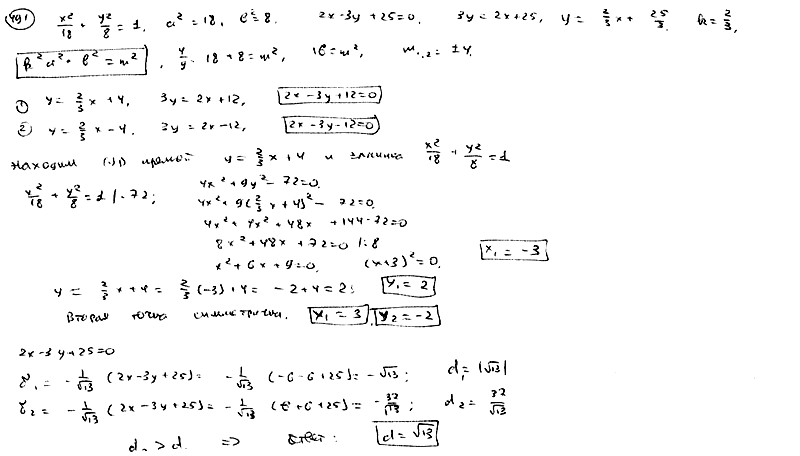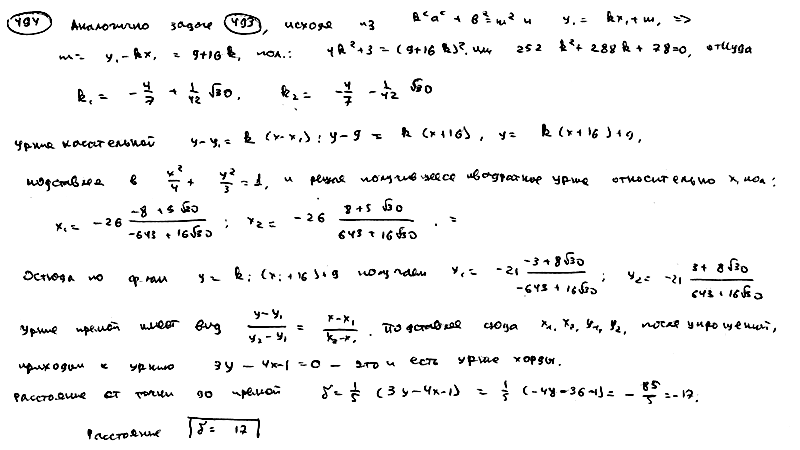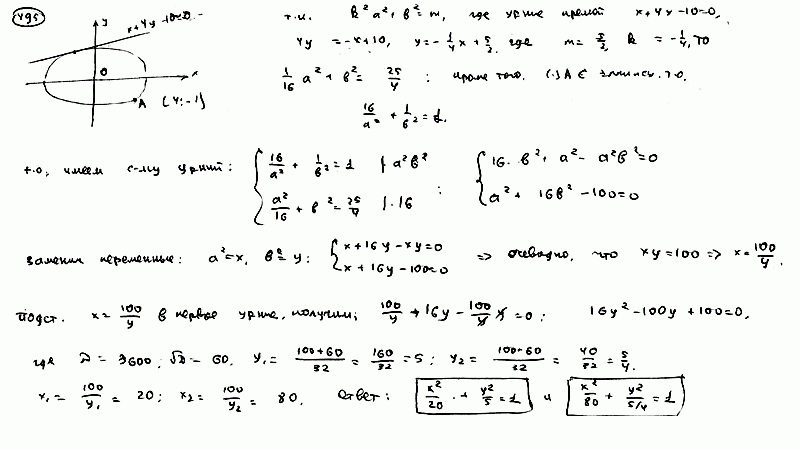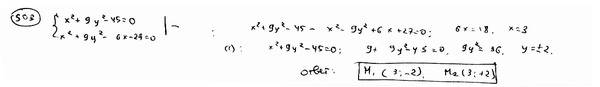Глава 18. Эллипс

444

Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:

444.1

его полуоси ранвы 5 и 2;

444.2

его большая ось равна 10, а расстояние между фокусами 2c=8;

444.3

его малая ось равна 24, а расстояние между фокусами 2c=10;

444.4

расстояние между его фокусами 2c=6 и эксцентриситет e=3/5.

444.5

его большая ось равна 20, а эксцентриситет e=3/5.

444.6

его малая ось равна 10, а эксцентриситет e=12/13;

444.7

расстояние между его директрисами равно 5 и расстояние между фокусами 2c=4;

444.8

его большая ось равна 8, а расстояние между директрисами равно 16;

444.9

его малая ось равна 6, а расстояние между директрисами равно 13;

444.10

расстояние между его директрисами равно 32 и e=1/2.

445

Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично начала координат, зная, кроме того, что:

445.1

его полуоси равны соответственно 7 и 2;

445.2

его большая ось равна 10, а расстояние между фокусами 2c=8;

445.3

расстояние между его фокусами 2c=24 и эксцентриситет e=12/13.

445.4

его малая ось равна 16, а эксцентриситет e=3/5.

445.5

расстояние между его фокусами 2c=6 и расстояние между директрисами равно 50/3;

445.6

расстояние между его директрисами равно 32/3 и эксцентриситет e=3/4.

446

Определить полуоси каждого из следующих эллипсов:

446.1

 ;

446.2

;

446.3

;

446.4

;

446.5

 ;

446.6

;

446.7

;

446.8

;

446.9

;

446.10

.

447

Дан эллипс . Найти его полуоси, фокусы, эксцентриситет, уравнения директрис.

448

Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса , а две другие совпадают с концами его малой оси.

449

Дан эллипс . Найти его полуоси, фокусы, эксцентриситет, уравнения директрис.

450

Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса , две другие лежат с концами его малой оси.

451

Вычислить расстояние от фокуса F(c; 0) эллипса до односторонней с этим фокусом директрисы.

452

Пользуясь одним циркулем, построить фокусы эллипса (считая, что изображены оси координат и задана масштабная единица).

453

На эллипсе найти точку, абсцисса которых равна –3.

454

Определить, какие из точек A₁(-2; 3), A₂(2; -2), A₃(2; -4), A₄(-1; 3), A₅(-4; -3), A₆(3; -1), A₇(3; -2), A₈(2; 1), A₉(0; 15), A₁₀(0; -16) лежат на эллипсе , какие внутри и какие вне его.

455

Установить, какие линии опеределяются следующими уравнениями. Изобразить эти линии на чертеже.

455.1

;

455.2

;

455.3

;

455.4

.

456

Эксцентриситет эллипса e=2/3, фокальный радиус точки М эллипса равен 10. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.

457

Эксцентриситет эллипса e=2/5, расстояние от точки эллипса до директрисы равно 20. Вычислить расстояние от точки М до фокуса, односторонней с этой директрисой.

458

Дана точка М₁(2; -5/3) на эллипсе ; составить уравнения прямых, на которых лежат фокальные радиусы точки М₁.

459

Убедившись, что точка M₁(-4; 2,4) лежит на эллипсе , определить фокальные радиусы точки М₁.

460

Эксцентриситет эллипса e=1/3, центр его совпадает с началом координат, один из фокусов (-2; 0). Вычислить расстояние от точки М₁ эллипса с абсциссой, равной 2, до директрисы, односторонней с данным фокусом.

461

Эксцентриситет эллипса e=1/2, центр его совпадает с началом координат, одна из директрис дана уравнением x=16. Вычислить расстояние от точки M₁ эллипса с абсциссой, равной –4, до фокуса, одностороннего с данной директрисой.

462

Определить точки эллипса , расстояние которых до правого фокуса равно 14.

463

Определить точки эллипса , расстояние которых до левого фокуса равно 2,5.

464

Через фокус эллипса проведен перпендикуляр к его большой оси. Определить расстояния от точек пересечения этого перпендикуляра с эллипсом до фокусов.

465

Составить уравнения эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если даны:

465.1

точка М₁(; 2) эллипса и его малая полуось b=3;

465.2

точка М₁(2; -2) эллипса и его большая полуось a=4;

465.3

точки М₁(4; ) и М₂(; 3) эллипса;

465.4

точка М₁(; -1) эллипса и его эксцентриситет e=2/3;

465.5

точка М₁(2; -5/3) эллипса и его эксцентриситет e=2/3;

465.6

точка М₁(8; 12) эллипса и расстояние r₁=20 от нее до левого фокуса.

465.7

точка М₁(; 2) эллипса и расстояние между его директрисами, равное 10.

466

Определить эксцентриситет e эллипса, если:

466.1

его малая ось видна из фокусов под углом 60⁰;

466.2

отрезок между фокусами виден и вершин малой оси под прямым углом;

466.3

расстояние между директрисами в три раза больше расстояния между фокусами;

466.4

отрезок перпендикуляра, опущенного из центра эллипса на его директрису, делится вершиной эллипса пополам.

467

Через фокус F эллипса проведен перпендикуляр к его большой оси (см. рис.). Определить, при каком значении эксцентриситета эллипса отрезки ибудут параллельны.

468

Составить уравнение эллипса с полуосями a, b и центром C(x₀, y₀), если известно, что оси симметрии эллипса параллельны осям координат.

469

Эллипс касается оси абсцисс в точке А(3; 0) и оси ординат в точке В(0; -4). Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.

470

Точка С(-3; 2) является центром эллипса, касающегося обеих координатных осей. Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.

471

Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет и уравнения директрис:

471.1

;

471.2

;

471.3

.

472

Установить, какие линии определяются следующими уравнениями. Изобразить эти линии на чертеже.

472.1

 ;

472.2

;

472.3

;

472.4

.

473

Составить уравнение эллипса, зная, что:

473.1

его большая ось равна 26 и фокусы суть F₁(-10; 0), F₂(14;0);

473.2

его малая ось равна 2 и фокусы суть F₁(-1; -1), F₂(1; 1);

473.3

его фокусы суть F₁(-2; 3/3), F₂(2; -3/2) и эксцентриситет e=.

473.4

его фокусы суть F₁(1; 3), F₂(3; 1) и расстояние между директрисами равно .

474

Составить уравнение эллипса, если известны его эксцентриситет , фокусF (-4; 1) и уравнение соответствующей директрисы

475

Составить уравнение эллипса, если известны его эксцентриситет e=1/2, фокус F(-4; 1) и уравнение соответствующей директрисы .

476

Точка А(-3; -5) лежит на эллипсе, фокус которого F(-1; -4), а соответствующая директриса дана уравнением . Составить уравнение этого эллипса.

477

Составить уравнение эллипса, если известны его эксцентриситет e=1/2, фокус F(3; 0) и уравнение соответствующей директрисы .

478

Точка M₁(2; -1) лежит на эллипсе, фокус которого F(1; 0), а соответствующая директриса дана уравнением . Составить уравнение этого эллипса.

479

Точка M₁(3; -1) является концом малой оси эллипса, фокусы которого лежат на прямой . Составить уравнение этого эллипса, зная его эксцентриситет e=.

480

Найти точки пересечения прямой и эллипса.

481

Найти точки пересечения прямой и эллипса.

482

Найти точки пересечения прямой и эллипса.

483

Определить, как расположена прямая относительно эллипса: пересекает ли, касается или проходит вне его, если прямая и эллипс заданы следующими уравнениями:

483.1

, ;

483.2

, ;

483.3

, .

484

Определить, при каких начениях m прямая :

484.1

пересекает эллипс ;

484.2

касается его;

484.3

проходит вне этого эллипса.

485

Вывести условие, при котором прямая касается эллипса.

486

Составить уравнение касательной к эллипсу в его точке M₁(x₁; y₁).

487

Доказать, что касательные к эллипсу , проведенные в концах одного и того же диаметра, параллельны. (Диаметром эллипса называется его хорда, проходящая через его центр).

488

Составить уравнения касательных к эллипсу, параллельных прямой.

489

Составить уравнения касательных к эллипсу , перпендикулярных к прямой.

490

Провести касательные к эллипсу параллельно прямойи вычислить расстояние d между ними.

491

На эллипсе найти точку М₁, ближайшую к прямой , и вычислить расстояние d от точки М₁ до этой прямой.

492

Из точки А(10/3; 5/3) проведены касательные к эллипсу . Составить их уравнения.

493

Из точки С(10; -8) проведены касательные к эллипсу . Составить уравнение хорды, соединяющей точки касания.

494

Из точки Р(-16; 9) проведены касательные к эллипсу . Вычислить расстояние d от точки Р до хорды эллипса, соединяющей точки касания.

495

Эллипс проходит через точку А(4; -1) и касается прямой . Составить уравнение этого эллипса при условии, что его оси совпадают с осями координат.

496

Составить уравнение эллипса, касающегося двух прямых ,, при условии, что его ося совпадают с осями координат.

497

Доказать, чо произведение расстояний от центра эллипса до точки пересечения любой его касательной с фокальной осью и до основания перпендикуляра, опущенного из точки касания на фокульную ось, если величина постоянная, равная квадрату большой полуоси эллипса.

498

Доказать, что произвдение расстояний от фокусов до любой касательной к эллипсу равно квадрату малой полуоси.

499

Прямая касается эллипса, фокусы которого находятся в точках F₁(-3; 0), F₂(3; 0). Составить уравнение этого эллипса.

500

Составить уравнение эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если известны уравнение касательной к эллипсу и его малая полуось b=2.

501

Доказать, что прямая, касающаяся эллипса в некоторой точке М, составляет равные углы с фокальными радиусами F₁M, F₂M и проходит вне угла F₁MF₂.

502

Из левого фокуса эллипса под тупым угломк оси Ox направлен луч света. Известно, что. Дойдя до эллипса, луч на него отразился. Составить уравнение прямой, на которой лежит отраженный луч.

503

Определить точки пересечения эллипсов ,.

504

Убедившись, что эллипсы ,() пересекаются в четырех точках, лежающих на окружности с центром в начале координат, определить радиус R этой окружности.

505

Плоскости иобразуют угол=30⁰. Опредлить полуоси эллипса, полученного проектированием на плоскость окружности радиуса R=10,лежащей на плоскости.

506

Эллипс, малая полуось которого равна 6, является проекцией окружности радиуса R=12. Опредилть угол между плоскостями, в которых лежат эллипс и окружность.

507

Направляющей круглого цилиндра является окружность радиуса R=8. Определить полуоси эллипса, полученного в сечении этого цилиндра плоскостью, наклоненной к его оси под уголом =30⁰.

508

Направляющей круглого цилиндра является окружность радиуса R=. Определить, под каким углом к оси цилиндра нужно его пересечь плоскостью, чтобы в сечении получить эллипс с большой полуосью a=2.

509

Равномерным сжатием (или равномерным растяжением) плоскости к оси абсцисс называется такое преобразование точек плоскости, при котором произвольная точка M(x; y) перемещается в точку M’(x’; y’) (рис.1 ) так, что x’=x, y’=qy, где q>0 – постоянная, называемая коэффициентом равномерного сжатия. Аналогично рпи помощи уравнения x’=qx, y’=y определяется равномерное сжатия плоскости к оси Oy (рис. 2). Определить, в какую линию преобразуется окружность , если коэффициент равномерного сжатия плоскости к оси абсцисс q=4/5.

510

Коэффициент равномерного сжатия плоскости к оси Oy равен 3/4. Определить уравнение линии, в которую при таком сжатии преобразуется эллипс .

511

Найти уравнение линии, в которую преобразуется эллипс при двух последовательных равномерных сжатиях плоскости к координатным осям, если коэффициенты равномерного сжатия плоскости к осям Ox и Oy равны соответственно 4/3 и 6/7.

512

Определить коэффициент q равномерного сжатия плоскости к оси Ox, при котором эллипс преобразуется в эллипс.

513

Определить коэффициент q равномерного сжатия плоскости к оси Oy, при котором эллипс преобразуется в эллипс.

514

Определить коэффициенты q₁, q₂ двух последовательных равномерных сжатий плоскости к осям Ox и Oy, при которых эллипс преобразуется в окружность.