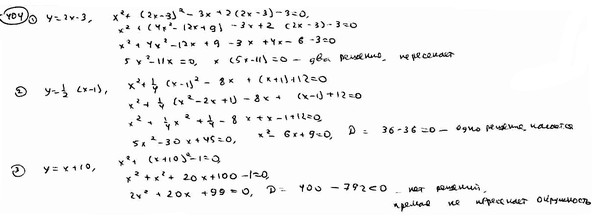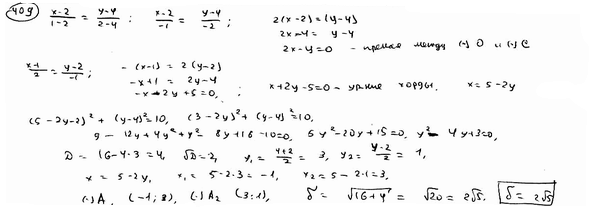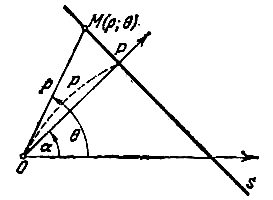
Глава 16. Полярное уравнение прямой

380

Вывести полярное уравнение прямой, зная ее расстояние от полюса p и полярный угол нормали .

Задача 0380

РЕШЕНИЕ. 1-Й СПОСОБ. На данной прямой s (рис.) возьмем произвольную точку М с полярными координатами и. Точку пересечения прямой s с ее нормалью обозначим буквой Р. Из прямоугольного треугольника ОРМ находим:

(1)

Мы получили уравнение с двумя переменными и, которму удовлетворяют координаты всякой точки М, лежащей на прямой s, и не удовлетворяют координаты никакой точки, не лежащей на этой прямой. Следовательно, уравнение (1) является уравнением прямой. Таким образом, задача решена.

2-Й СПОСОБ. Будем рассматривать декартову прямоугольную систему координат, положительная полуось абсцисс которой совпадает с полярной осью заданной полярной системы. В этой декартовой системе имеем нормальное уравнение прямой s:

(2)

Воспользуемся формулами преобразования полярных координат в декартовы:

, (3)

Подставив в уравнение (2) вместо х и у выражения (3), получим

или

.

381

Вывести полярное уравнение прямой, если даны:

381.1

Угол наклона прямой к полярной оси и длину перпендикуляра p,опущенного из полюса на эту пряму; написать уравнение этой прямой в случае, p=3;

381.2

Отрезок а, который отсекает прямая на полярной оси, осчитая от полюса, и полярный угол нормали этой прямой; написать уравнение этой прямой в случае а=2;;

381.3

Угол наклона прямой к полярной оси и отрезок а, который отекает прямая на полярной оси, считая от полюса; написать уравнение этой прямой в случае, а=6.

382

Вывести полярное уравнение прямой, проходящей через точку M₁(;) и наклоненной к полярной оси под углом.

383

Вывести полярное уравнение прямой, проходящей через точку M₁(;), полярный угол нормали которой равен.

384

Составить уравнение прямой, проходящей через точки M₁(;) и M₂(;).

385

Составить уравнение окружности в каждом из следующих случаев:

385.1

центр окружности совпадает с началом координат и ее радиус R=3;

385.2

центр окружности совпадает с точкой С(2; -3) и ее радиус R=7;

385.3

окружность проходит через начало координат и ее центр совпадает с точкой С(6; -8);

385.4

окружность проходит через точку А(2; 6) и ее центр совпадает с точкой С(-1; 2);

385.5

точки А(3; 2) и В(-1; 6) являются концами одного из диаметров окружности;

385.6

центр окружности совпадает с началом координат и прямая является касательной к окружности;

385.7

центр окружности совпадает с точкой С(1; -1) и прямая является касательной к окружности;

385.8

окружность проходит через точки А(3; 1) и В(-1; 3), а ее центр лежит на прямой ;

385.9

окружность проходит через три точки А(1; 1), В(1; -1), С(2; 0);

385.10

окружность проходит через три точки: М₁(-1; 5), М₂(-2; -2). М₃(5; 5).

386

Точка С(3; -1) является центром окружности, отсекающей на прямой хорду, длина которой равна 6. Составить уравнение этой окружности.

387

Написать уравнения окружностей радиуса , касающихся прямойв точке М₁(3; 1).

388

Составить уравнение окружности, касающейся прямых ,, причем одна из них – в точке А(2; 1).

389

Составить уравнения окружностей, которые проходят через точку А(1; 0) и касаются прямых ,.

390

Составить уравнение окружности, которая, имея центр на прямой , касается прямых,.

391

Составить уравнения окружностей, касающихся прямых ,, причем одной из них – в точке М₁(1; 2).

392

Составить уравнения окружностей, проходящих через начало координат и касающихся прямых ,.

393

Составить уравнение окружностей, которые, имея центры на прямой , касаются прямых,.

394

Написать уравнения окружностей, проходящих через точку А(-1; 5) и касающихся прямых ,.

395

Написать уравнения окружностей, касающихся прямых ,,.

396

Написать уравнения окружностей, касающихся прямых ,,.

397

Какие из нижеприводимых уравнений определяют окружности? Найти центр С и радиус R каждой из них:

397.1

 ;

397.2

 ;

397.3

;

397.4

;

397.5

;

397.6

;

397.7

;

397.8

;

397.9

;

397.10

 .

398

Установить, какие линии определяются следующими уравнениями. Изобразить эти линии на чертеже.

398.1

;

398.2

;

398.3

;

398.4

;

398.5

;

398.6

;

398.7

;

398.8

;

398.9

 ;

398.10

.

399

Установить, как расположена точка А(1; -2) относительно каждой из следующих окружностей – внутри, вне или на контуре:

399.1

;

399.2

;

399.3

;

399.4

;

399.5

.

400

Определить уравнение линии центров двух окружностей, заданных уравнениями:

400.1

и ;

400.2

и ;

400.3

и ;

400.4

и .

401

Составить уравнение диаметра окружности , перпендикулярного к прямой.

402

Вычислить кратчайшее расстояние от точки до окружности в каждом из следующих случаев:

402.1

А(6; -8), ;

402.2

В(3; 9), ;

402.3

С(-7; 2), .

403

Определить координаты точек пересечения прямой и окружности.

404

Определить, как расположена прямая относительно окружности (пересекает ли, касаетлся или проходит вне ее), если прямая и окружность заданы следующими уравнениями:

404.1

 , ;

404.2

 , ;

404.3

, .

405

Определить, при каких значениях углового коэффициента k прямая :

405.1

пересекает окружность ;

405.2

касается этой окружности;

405.3

проходит вне этой окружности.

406

Вывести условие, при котором прямая касается окружности.

407

Составить уравнние диаметра окружности , проходящего через середину хорды, отсекаемой на прямой.

408

Составить уравнение хорды окружности , делящейся в точке М(8,5; 3,5) пополам.

409

Определить длину хорды окружности , делящейся в точке А(1; 2) пополам.

410

Дано уравнение пучка прямых . Найти прямые этого пучка, на которых окружностьотсекает хорды длиною.

411

Даны окружности ,, пересекающиеся в точках М₁(x₁, y₁), М₂(x₂, y₂). Доказать, что любая окружность, проходящая через точки М₁, М₂, а также прямая М₁М₂ могут быть определены уравнением вида при надлежащем выборе числеи.

412

Составить уравнение окружности, проходящей через точку А(1; -1) и точки пересечения окружностей ,.

413

Составить уравнение окружности, проходящей через начало координат и точки пересечения окружностей ,.

414

Составить уравнение прямой, проходящей через точки пересечения окружностей ,.

415

Вычислить расстояние от центра окружности до прямой, проходящей через точки пересечения окружностей,.

416

Определить длину общей хорды окружностей ,.

417

Центр окружности лежит на прямой . Составить уравнение этой окружности, если известно, что она проходит через точки пересечения окружностей,.

418

Составить уравнение касательной к окружности в точке А(-1; 2).

419

Составить уравнение касательной к окружности в точке А(-5; 7).

420

На окружности найти точку М₁, ближайшую к прямой , и вычислить расстояние d от точки М₁ до этой прямой.

421

Точка М₁(x₁, y₁) лежит на окружности . Составить уравнение касательной к этой окружности в точке М₁.

422

Точка М₁(x₁, y₁) лежит на окружности . Составить уравнение касательной к этой окружности в точке М₁.

423

Определить острый угол, образованный при пересечении прямой и окружности(углом между прямой и окружности называется угол между прямой и касательной к окружности, проведенной к точке их пересечения).

424

Определить, при каким углом пересекаются окружности ,(углом между окружностями называется угол между их касательными в точке пересечения).

425

Вывести условие, при котором окружности,пересекаются под прямым углом.

426

Доказать, что окружности ,пересекаются под прямым углом.

427

Из точки А(5/3; -5/3) проведены касательной к окружности . Составить их уравнения.

428

Из точки А(1; 6) проведены касательные к окружности . Составить их уравнения.

429

Дано уравнение пучка прямых . Найти прямые этого пучка, которые касаются окружности.

430

Из точки А(4; 2) проведены касательные к окружности . Определить угол, образованный этими касательными.

431

Из точки Р(2; -3) проведены касательные к окружности . Составить уравнение хорды, соединяющий точки касания.

432

Из точки С(6; -8) проведены касательные к окружности . Вычислить расстояние d от точки С до хорды, соединяющей точки касания.

433

Из точки Р(-9; 3) проведены касательные к окружности . Вычислить расстояние d от центра окружности до хорды, соединяющей точки касания.

434

Из точки Р(4; -4) проведены касательные к окружности . Вычислить длину d хорды, соединяющей точки касания.

435

Вычислить длину касательной, проведенной из точки А(1; -2) к окружности .

436

Составить уравнение касательных к окружности , параллельных прямой.

437

Составить уравнения касательных к окружности , перпендикулярных к прямой.

438

Составить уравнение окружности в полярных координатах в полярных координатах по данному радиусу R и полярным координатам центра C(R, ).

439

Составить уравнение окружности в полярных координатах по данному радиусу R и полярным координатам центра окружности:

439.1

C(R, 0);

439.2

C(R, );

439.3

C(R, );

439.4

C(R, ).

440

Определить полярные координаты центра и радиус каждой из следующих окружностей:

440.1

 ;

440.2

;

440.3

;

440.4

 ;

440.5

;

440.6

;

440.7

 ).

441

Окружности заданы уравнениями в полярных координатах. Составить их уравнения в декартовых прямоугольных координатах при условии, что полярная ось совпадает с положительной полуосью Ох, а полюс – с началом координат.

441.1

 ;

441.2

;

441.3

.

442

Окружности заданы уравнениями в декартовых прямоугольных координатах. Составить уравнения этих окружностей в полярных координатах при условии, что полярная ось совпадает с положительной полуосью Ох, а полюс – с началом координат.

442.1

;

442.2

;

442.3

;

442.4

;

442.5

.

443

Составить полярное уравнение касательной к окружности в точке М₁(R, ).