Классификация резисторов

По зависимости ВАХ от внешних условий:

• постоянные резисторы — номинал сопротивления не управляется,

• переменные управляемые резисторы:

  • потенциометры,

  • реостаты,

  • подстроечные резисторы

• специальные резисторы, например:

  • нелинейные — ВАХ нелинейна,

  • терморезисторы — сопротивление зависит от температуры,

  • фоторезисторы — сопротивление зависит от освещённости,

  • тензорезисторы — сопротивление зависит от деформации резистора,

  • магниторезисторы — сопротивление зависит от величины магнитного поля.

По технологии изготовления:

• Проволочные резисторы. Представляют собой кусок проволоки с высоким удельным сопротивлением намотанный на какой-либо каркас. Могут иметь значительную паразитную индуктивность. Высокоомные малогабаритные проволочные резисторы иногда изготавливают из микропровода.

• Плёночные металлические резисторы. Представляют собой тонкую плёнку металла с высоким удельным сопротивлением, напылённую на керамический сердечник, на концы сердечника надеты металлические колпачки с проволочными выводами. Иногда, для повышения сопротивления, в плёнке прорезается винтовая канавка. Это наиболее распространённый тип резисторов.

• Металлофольговые резисторы. В качестве резистивного материала используется тонкая металлическая лента.

• Угольные резисторы. Бывают плёночными и объёмными. Используют высокое удельное сопротивление графита.

• Интегральный резистор. Используется сопротивление слаболегированного полупроводника. Эти резисторы могут иметь большую нелинейность вольт-амперной характеристики. В основном используются в составе интегральных микросхем, где применить другие типы резисторов невозможно или не технологично.

Резисторы, выпускаемые промышленностью

Выпускаемые промышленностью резисторы одного и того же номинала имеют разброс сопротивлений. Значение возможного разброса определяется точностью резистора. Выпускают резисторы с точностью 20 %, 10 %, 5 %, и т. д. вплоть до 0,01 %. Номиналы резисторов не произвольны: их значения выбираются из специальных номинальных рядов, наиболее часто из номинальных рядов E6 (20 %), E12 (10 %) или E24 (для резисторов с точностью до 5 %), для более точных резисторов используются более точные ряды (например E48).

Резисторы, выпускаемые промышленностью характеризуются также определённым значением максимальной рассеиваемой мощности (выпускаются резисторы мощностью 0,125Вт 0,25Вт 0,5Вт 1Вт 2Вт 5Вт) (Согласно ГОСТ 24013-80 и ГОСТ 10318-80 советской радиотехнической промышленностью выпускались резисторы следующих номиналов мощностей, в Ваттах, Вт.: 0.01, 0.025, 0.05, 0.062, 0.125, 0.5, 1, 2, 3, 4, 5, 8, 10, 16, 25, 40, 63, 100, 160, 250, 500).

Маркировка резисторов с проволочными выводами

Резисторы, в особенности малой мощности — чрезвычайно мелкие детали, резистор мощностью 0,125Вт имеет длину несколько миллиметров и диаметр порядка миллиметра. Прочитать на такой детали номинал с десятичной запятой невозможно. Поэтому, при указании номинала вместо десятичной точки пишут букву, соответствующую единицам измерения (К — для килоомов, М — для мегаомов, E или R для единиц Ом). Например 4K7 обозначает резистор, сопротивлением 4,7 кОм, 1R0 — 1 Ом, 120К — 120 кОм и т. д. Однако и в таком виде читать номиналы трудно. Поэтому, для особо мелких резисторов применяют маркировку цветными полосками.

Для резисторов с точностью 20 % используют маркировку с тремя полосками, для резисторов с точностью 10 % и 5 % маркировку с четырьмя полосками, для более точных резисторов с пятью или шестью полосками. Первые две полоски всегда означают первые два знака номинала. Если полосок 3 или 4, третья полоска означает десятичный множитель, то есть степень десятки, которая умножается на двузначное число, указанное первыми двумя полосками. Если полосок 4, последняя указывает точность резистора. Если полосок 5, третья означает третий знак сопротивления, четвёртая — десятичный множитель, пятая — точность. Шестая полоска, если она есть, указывает температурный коэффициент сопротивления (ТКС). Если эта полоска в 1,5 раза шире остальных, то она указывает надёжность резистора (% отказов на 1000 часов работы)

Следует отметить, что иногда встречаются резисторы с 5 полосами, но стандартной (5 или 10 %) точностью. В этом случае первые две полосы задают первые знаки номинала, третья — множитель, четвёртая — точность, а пятая — температурный коэффициент.

Цветовая кодировка резисторов
Цвет	как число	как десятичный множитель	как точность в %	как ТКС в ppm/°C	как % отказов
серебристый	—	1·10−2 = «0,01»	10	—	—
золотой	—	1·10−1 = «0,1»	5	—	—
чёрный	0	1·100 = 1	—	—	—
коричневый	1	1·101 = «10»	1	100	1 %
красный	2	1·10² = «100»	2	50	0,1 %
оранжевый	3	1·10³ = «1000»	—	15	0,01 %
жёлтый	4	1·104 = «10 000»	—	25	0,001 %
зелёный	5	1·105 = «100 000»	0,5	—	—
синий	6	1·106 = «1 000 000»	0,25	10	—
фиолетовый	7	1·107 = «10 000 000»	0,1	5	—
серый	8	1·108 = «100 000 000»	—	—	—
белый	9	1·109 = «1 000 000 000»	—	1	—
отсутствует	—	—	20 %	—	—

По ссылке http://www.okaphone.nl/calc/russian.shtml?ohm=1k&tol=5 находится программа, которая переводит цветовую маркировку в символьные значения.

Пример

Допустим на резисторе видим 4 полоски коричневую, чёрную, красную, золотую. Первые две полоски дают 1 0, третья 100, четвёртая даёт точность 5 %, итого резистор сопротивлением 10·100 Ом = 1 кОм, с точностью ±5 %.

Поскольку резистор симметричная деталь, может возникнуть вопрос: «Начиная с какой стороны читать полоски?» Для четырёхполосной маркировки обычных резисторов с точностью 5 и 10 % вопрос решается просто: золотая или серебряная полоска всегда стоит в конце. Для трёхполосочного кода первая полоска стоит ближе к краю резистора, чем последняя. Для других вариантов важно, чтобы получалось значение сопротивления из номинального ряда, если не получается, нужно читать наоборот. (Для резисторов МЛТ-0,125 производства СССР с 4 полосками, первой является полоска, нанесённая ближе к краю; обычно она находится на металлическом стаканчике вывода, а остальные три — на более узком керамическом теле резистора).

SMD резисторы предназначены для поверхностного монтажа

SMD резисторы имеют следующие типоразмеры:

SMD резисторы можно купить на кардачах в павильоне 9-в

Делитель напряжения

Делитель напряжения – устройство для деления постоянного или переменного напряжения. Строится на основе активных и/или реактивных (реактивное сопротивление – сопротивление емкости или индуктивности переменному току) сопротивлений.

Ток протекающий в делителе напряжения рассчитывается по закону Ома:

Согласно тому же закону Ома, напряжение на выходе делителя (резистор R2) составит:

Таким образом, если мы знаем напряжение и произвольно выберем сопротивление одного из резисторов (R1 или R2), то по приведенной выше формуле можно вычислить сопротивление другого резистора, для получения необходимого напряжения на выходе делителя. На самом деле, сопротивления R1 и R2 выбираются далеко не произвольно, поскольку существует такое понятие как согласование схем по напряжению. И если мы хотим, чтобы напряжение на выходе ненагруженной схемы равнялось напряжению нагруженной схемы, необходимо чтобы сопротивление нагрузки (входное сопротивление следующей схемы) было намного меньше выходного сопротивления аналоговой схемы. Согласование схем будет рассмотрено в следующем разделе.

Потенциометр – переменный резистор, который фактически представляет собой варьируемый делитель напряжения.

Согласование схем – согласование источника и нагрузки

Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:

• Согласование по напряжению — получение в нагрузке максимального напряжения. Для этого сопротивление нагрузки должно быть как можно бо́льшим, по крайней мере, много больше, чем внутреннее сопротивление источника. При этом максимально достижимое в нагрузке напряжение равно ЭДС генератора напряжения. Данный тип согласования применяется в электронных системах, когда носителем сигнала является напряжение, и его необходимо передать от источника к нагрузке с минимальными потерями. Поэтому генератор должен иметь выходное сопротивление намного меньше, чем входное сопротивление подключаемой к генератору схемы. Тоже самое, если ко входу аналоговой схемы подключается датчик. В таком случае входное сопротивление схемы должно быть намного больше сопротивления датчика;

• Согласование по току — получение в нагрузке максимального тока. Для этого сопротивление нагрузки должно быть как можно меньшим, по крайней мере, много меньше, чем внутреннее сопротивление источника. При этом максимально достижимый в нагрузке ток равен I_max=E/r. Применяется в электронных системах, когда носителем сигнала является ток. Например, при съеме сигнала с быстродействующего фотодиода целесообразно применять преобразователь ток-напряжение с минимальным входным сопротивлением;

• Согласование по мощности — обеспечивает передачу от источника в нагрузку максимально возможной мощности, равной P_max=E²/(4r). В цепях постоянного тока: сопротивление нагрузки должно быть равно внутреннему сопротивлению r источника. Поэтому для достижения наибольшей громкости звучания, сопротивление динамика (нагрузки) должно равняться выходному сопротивлению усилителя.

Пример:

Допустим, есть аналоговая схема с выходным сопротивлением R_вых и напряжением холостого хода (без нагрузки) – E. Найти при каком сопротивлении загрузки R, в загрузку будет передана максимальная мощность.

Напряжение на нагрузке рассчитывается по формуле:

Мощность, что выделится на нагрузке сопротивлением R:

Для определения значения , при котором максимальна, решим уравнение . Где - производная.

, когда ->

->

Итак, теперь очевидно, что максимальная мощность передается в нагрузку, когда сопротивление нагрузки равно выходному сопротивлению схемы.

Теперь, когда мы станем проектировать источник напряжения в виде делителя, мы знаем, что для согласования по напряжению, сопротивление нагрузки на делитель должно быть намного больше выходного сопротивления делителя. В противном случае, напряжение нагруженного делителя будет значительно меньше, чем напряжение на выходе делителя в режиме холостого хода. В этом то и состоит проблема источников напряжения в виде делителей (типа подаем на вход 20 вольт, а на выходе делителя снимаем 5 В). Для согласования по напряжению, сопротивления делителя должны быть небольшие (чтобы обеспечить малое выходное сопротивление делителя). Через эти маленькие сопротивления делителя, согласно закону Ома будет протекать большой ток, а это – большая потребляемая мощность. Получается очень неэффективно. Если питать такое устройство от батарейки, то батарейка очень быстро “сядет”.

Конденсатор

Конденсатор – это устройство способное накапливать заряд.

Q = C·U

Соответственно, чем больше емкость конденсатора и чем больше приложенное к конденсатору напряжение, тем больший заряд будет накоплен на обкладках конденсатора.

Конденсатор, имеющий емкость С фарад, к которому приложено напряжение U вольт, накапливает заряд Q кулон на одной пластине и -Q на другой.

Поскольку ток – это изменение заряда в проводнике за единицу времени, продифференцировав выражение для заряда на конденсаторе получим формулу, описывающую проходящий через конденсатор ток.

Единица измерения емкости – Фарада. Это очень большая величина, поэтому на практике используют микрофарады (мкФ), пикофарады (пФ) и нанофарады (нФ).

При параллельном соединении конденсаторов их емкость складывается

С=С1+С2+С3+…+Сn

Емкость последовательно соединенных конденсаторов равна:

Похоже на формулу для параллельного соединения резисторов, правда? 

Ток, заряжающий конденсатор (I = CdU/dt),обладает некоторыми особыми свойствами. В отличие от тока, протекающего через резистор, он пропорционален не напряжению, а скорости изменения напряжения (т.е. его производной по времени). Далее, мощность (U·I), которая связана с протекающим через конденсатор током, не обращается в тепло, а сохраняется в виде энергии внутреннего электрического поля в конденсаторе. При разряде конденсатора происходит извлечение энергии.

RC цепочка

Заряд конденсатора

Рассмотрим простейшую RC цепочку.

В соответствии с первым законом Кирхгофа ток в цепи будет равняться:

I = C(dU/dt) = - U/R;

Это выражение представляет собой дифференциальное уравнение, решение которого имеет вид:

U = U₀ e ^{- t/RC}

Отсюда следует, что если заряженный конденсатор подключить к резистору, то он будет разряжаться так, как показано на рисунке.

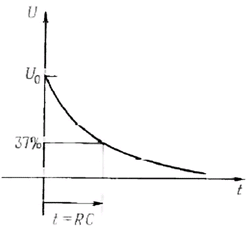
Постоянная времени. Произведение RC называют постоянной времени цепи. Постоянную времени обычно обозначают буквой t или. сли R измерять в омах, а С - в фарадах, то произведение RC будет измеряться в секундах. Физический смысл постонной времени – за время , напряжение на конденсаторе уменьшается в е=2.7 раза. Конденсатор полностью заряжается за время . Таким образом, если вы хотите, чтобы конденсатор зарядился за определенное время Т, зная емкость конденсатора, можно вычислить сопротивление резистора из уравнения -> -> .

Заряд конденсатора

Уравнение, описывающее работу такой схемы, выглядит следующим образом:

I = C(dU/dt) = (U_вх - U)/R.

и имеет решение

U = U_вх(1 - e ^-t/RC)

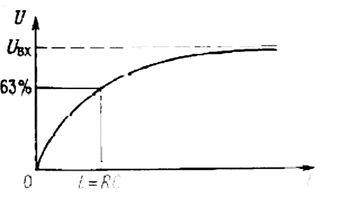
На рисунке ниже показаны временные диаграммы заряда/разряда конденсатора