
tmech_stat
.pdf
11 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
M |
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
P |
|
А |
В |
|
C |
D |
|
|
M |
|
|
|||
|
|
|
|
|
α |
|
||||||
|
|
|
|
|
|
P |
А |
В |
|
C |
D |
|
α |
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
13 |
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
q |
|
|
|
|
|
|
|
А |
|
C |
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
В |
|
|
|
D |
|
|
|
|
q |
|
|
|
|
|
|
|
||
А |
M |
|
C |
α |
D |
G |
P α |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
В |
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
16 |
|
|
|
|
|
|
|
q |
|
M |
|
|
α |
|
P |
|
M |
|
q |
|
|
|
|
|
|
|
|
|
||||
|
В |
|
C |
|
D |
|
|
β |
|
|
|
D |
А |
|
|
|
α |
|
|
А |
В |
|
C |
|
|
17 |
|
|
q |
|
|
18 |
|
|
|
|
|
|
|
M |
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
||
А |
В |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
P |
|
|
q |
|||
|
|
|
|
|
D |
|
|
M |
|
|||
α |
|
|
|
|
G |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
β |
|
C |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
В |
|
|
D |
19 |
|
|
|
|
|
20 |
P |
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
P |
M |
q |
|
|
|
А |
В |
|
M |
|
|
|
β |
|
|
α |
G |
|
|
|
|
|
||
А |
|
|
|
|
|
|
|
|
q |
|||
|
В |
|
C |
D |
|
|
|
|
|
C |
β |
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.3.1,б |
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
21 |
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
q |
P |
|
|
|
|
|
|
E |
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
M |
|
||
|
|
α |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
D |
|
|
|
|
|
|
||
|
|
|
|
|
|
β |
|
|
|
|
|
||
|
|
|
|
|
|
А |
В |
|
C |
|
D |
||
А |
|
В |
C |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
β |
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
23 |
|
|
|
|
|
|
24 |
|
|
|
|
|
|
А |
M |
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
В |
|
|
|
|
|
|
В |
|
C |
|
M |
|
|
|
C |
|
|
|
|
|
|
|
|
||
|
|
|
β |
|
|
|
А |
|
|
|
|
D |
|
|
|
q |
|
|
|
G |
|
|
|
|
|||
|
|
|
D |
|
|
|
|
|
α |
P |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
M |
q |
P |
α |
|
|
|
M |
P |
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
C |
|
|
|
А |
|
В |
|
C |
D |
|
|
В |
|
|
|
D |
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
M |
|
q |
|
|
|
28 |
|
|
|
|
q |
D |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
А |
|
|
|
|
|
|
|
|
|
|
M |
|
β |
|
|
В |
C |
P β |
D |
|
|
В |
|
|
C |
||
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
α P |
|
|
|
|
29 |
|
q |
|
|
|
|
30 |
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
P |
|
|
|
||
|
|
|
|
|
|
|
|
M |
|
|
|||
|
|
|
M |
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
А |
В |
|
C |
D |
||
|
α |
|
|
|
|
|
|
|
|||||
|
В |
C |
|
P |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
β |
|
|
|
q |
|
|
|
q |
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.3.1,в |
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|

Приклад 3. Визначити опорні реакції балки, зображеної на рис. 3.2,
якщо P=10 кН, M 30 кН∙м, |
q 2 кН/м, |
60 , AB=3 м, BC=2 м, |
CD=2 м. |
|
|
q |
M P |
|
A |
α |
D |
B |
C |
|
Рис.3.2.
Розв’язання. Для розв’язання задачі потрібно дотримуватися наступної послідовності дій.
1.Виділяємо тіло, яке знаходиться у рівновазі. Таке тіло називають об'єктом дослідження. У даній задачі об'єктом дослідження є балка AD
(рис. 3.2).
2.Вказуємо задані (активні) сили, які прикладені до балки. На балку діє
зосереджена сила P , яка прикладена в точці C , пара сил з моментом М та рівномірно розподілене навантаження інтенсивністю q. Розподілене навантаження заміняємо еквівалентною силою Q. У даній задачі величину сили Q визначають як площу заштрихованої фігури, а її лінія дії проходить через центр ваги цієї фігури. Таким чином, маємо: Q = AB∙q = 3∙2 = 6 кН
(рис.3.3).
|
y |
|
|
RA |
Q |
M P |
YD |
|
q |
|
|
A |
|
α |
x |
B |
|
|
|
|
C |
D XD |
Рис.3.3.
23
3.Вводимо систему координат Axy, осі якої зв’язуємо з балкою AD
(рис.3.3).
4.Визначаємо механічні в’язі, накладені на тіло. Для балки в’язями є рухомий шарнір у точці А та нерухомий шарнір у точці D. Застосовуючи, аксіому про звільнення від в’язей, подумки відкидаємо в’язі, замінивши
їхню дію на тіло реакціями. Реакція рухомого шарніра RA у точці А напрямлена перпендикулярно до опорної поверхні. Реакція нерухомого шарніра у точці D подається як сума двох взаємоперпендикулярних складових RD X D YD , напрямлених вздовж координатних осей у бік їх додатніх значень (рис.3.3).
5. Проводимо аналіз системи сил, прикладених до балки. Очевидно, що ця система сил { P , Q, M , RA , X D, YD } є плоскою системою сил. Оскільки балка зрівноважена, то і дана система сил теж зрівноважена і для неї можна скласти три рівняння рівноваги. Зазначимо, що кількість невідомих сил: RA , X D, YD не перевищує кількості рівняннь рівноваги, тобто дана система сил є статично визначеною.
6. Складемо аналітичні рівняння рівноваги плоскої системи сил: два рівняння проекцій сил на осі вибраної системи координат та одне рівняння моментів сил відносно вибраної точки (полюса). Перші два рівняння записують як суми проекцій усіх сил, прикладених до балки, на відповідні осі і прирівнюють нулю:
n
Fix Pcos X D 0;i 1
n
Fiy RA Q Psin YD 0.i 1
Рівняння моментів сил складають так. Вибираємо точку (полюс), відносно якої будемо визначати моменти сил, наприклад, точку А. Далі
24

визначаємо послідовно моменти усіх сил, прикладених до балки, користуючись робочою формулою:
МА( F ) = hF,
де h – плече сили F, знак “+” відповідає уявному повороту балки від дії сили F навколо обраного полюса А проти стрілки годинника, знак “–“ – за стрілкою годинника.
Для сили RA маємо:
МА( RA ) = 0,
оскільки плече цієї сили відносно точки А дорівнює нулю. Моменти інших сил записуємо так:
МА(Q ) = – 0,5∙АВ∙Q,
МА( P ) = – AC∙sinα∙P,
МА( YD ) = AD∙YD , МА( X D ) = 0.
Оскільки пара сил, прикладених до балки, еквівалентна моменту, та можливий поворот балки може здійснити проти стрілки годинника, відповідний момент записуємо у вигляді доданка М. Таким чином, рівняння моментів сил має вигляд
|
n |
|
|
|
Q |
1 AB M Psin AC Y |
AD 0, |
|||
M |
|
|
||||||||
i 1 |
|
iA |
|
|
2 |
D |
|
|
||
і відповідно, система рівнянь рівноваги балки AD така |
|
|
||||||||
n |
|
|
|
Pcos X D 0; |
|
|
||||
|
Fix |
|
|
|||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
RA Q Psin YD 0; |
|
|
||||
|
Fiy |
|
|
|||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
n |
M |
|
|
Q |
1 |
AB M Psin AC Y |
|
AD 0. |
||
|
|
iA |
|
|||||||
|
|
|
|
|
2 |
D |
|
|||
i 1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
7. Розв’язуємо отримані рівняння і обчислюємо невідомі величини
25

X D Pcos 5кН;
YD AD1 (Q 12 AB M Psin AC) = 3,19 кН.
Підставляємо значення YD у друге рівняння
RA Q Psin YD 11,47 кН.
Значення повної реакції у точці D дорівнює
RD 
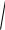 X D2 YD2 =5,93 кН.
X D2 YD2 =5,93 кН.
26
4. ВИЗНАЧЕННЯ РЕАКЦІЙ ОПОР СКЛАДЕНОЇ КОНСТРУКЦІЇ
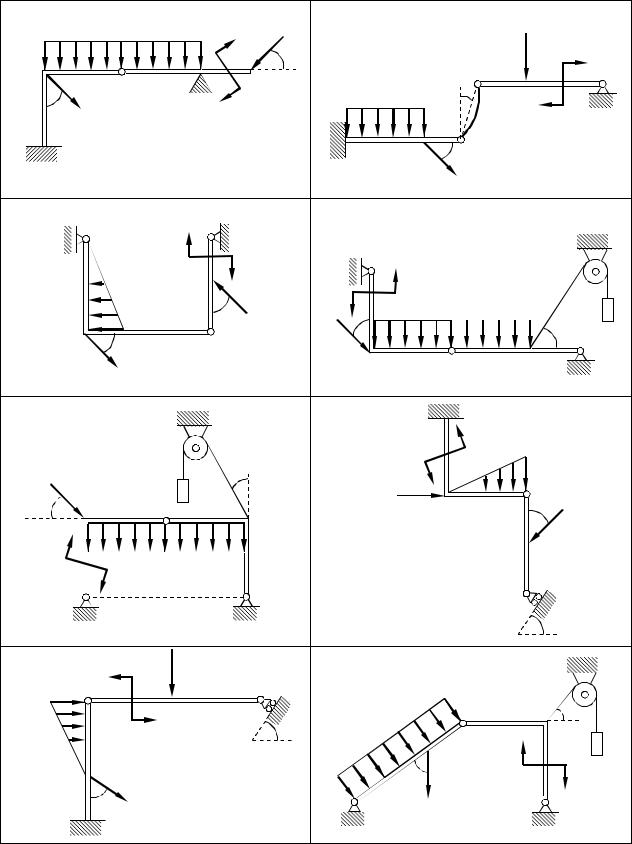
Конструкція складається з двох частин, з’єднаних між собою ідеальним шарніром С або ідеальним абсолютно жорстким стержнем С'С'' (рис.4.1). До конструкції, в залежності від номеру варіанта, прикладається: зосереджена сила Р1 та Р2 або сила Р1 та вантаж вагою G, який прикріпляється за допомогою невагомої нитки, перекинутої через блок; рівномірно розподілене навантаження інтенсивністю q або інтенсивності, що змінюється лінійно від нуля до максимального значення qmax.; пара сил з моментом М. Конструкцію вважати невагомою. Визначити реакції в’язей, якими є нерухомий або рухомий шарнір, жорстке защемлення, ідеальний абсолютно жорсткий стержень, опора у вигляді гладкого вістря. Чисельні дані подано у таблиці 4.
Приклад 4. Застосовуючи аналітичні умови рівноваги визначити опорні реакції конструкції, що складається з двох тіл (рис. 4.2). До конструкції прикладено рівномірно розподілене навантаження інтенсивністю q=2 Н/м, пара сил з моментом M 4 H∙м. У точці В до конструкції за допомогою невагомої нитки, перекинутої через блок, прикріпляється вантаж вагою G=5 Н (тертям у блоці знехтувати). Визначити опорні реакції RA , RE і силу тиску в точці C балок одна на одну, якщо AC = 2 м, BC = 2 м, CD = 3 м, DE=1 м, α=45°, β=30°.
Розв’язання. Для розв’язання задачі потрібно дотримуватися наступної послідовності дій.
1 . Розглянемо рівновагу усієї конструкції.
2. Проведемо аналіз активних сил, прикладених до конструкції: до неї прикладається пара сил з моментом М, та рівномірно розподілене вздовж ділянки BD навантаження (система паралельних сил) інтенсивністю q= =2 Н/м.
27
Таблиця 4
Варіант |
АВ |
ВС (BC') |
CD (C''D) |
DE |
α |
β |
P1 |
P2 (G) |
q (qmax) |
M |
|
|
|
м |
|
град |
|
кН |
кН/м |
КН∙м |
|
1 |
3 |
2 |
1,5 |
0,5 |
30 |
60 |
15 |
10 |
8 |
5 |
2 |
3 |
1 |
1,5 |
3 |
45 |
30 |
14 |
20 |
4 |
6 |
3 |
2 |
2,5 |
0,5 |
1,5 |
30 |
60 |
12 |
7 |
6 |
8 |
4 |
2 |
3 |
2,5 |
1,5 |
30 |
45 |
10 |
8 |
2 |
4 |
5 |
2 |
2,5 |
2 |
2 |
45 |
30 |
16 |
9 |
10 |
6 |
6 |
1,5 |
2 |
0,5 |
1,5 |
30 |
45 |
8 |
14 |
3,5 |
6 |
7 |
2 |
2 |
2 |
3 |
30 |
60 |
7 |
11 |
6 |
8 |
8 |
2,5 |
1,5 |
3 |
2 |
60 |
45 |
12 |
8 |
8 |
3 |
9 |
3 |
2 |
2 |
2 |
45 |
60 |
15 |
12 |
6 |
5 |
10 |
2 |
3 |
1,5 |
3,5 |
45 |
30 |
12 |
7 |
4 |
8 |
11 |
2 |
3 |
1,5 |
1,5 |
30 |
60 |
20 |
15 |
8 |
9 |
12 |
4 |
1,5 |
3 |
2 |
60 |
45 |
14 |
10 |
3 |
7 |
13 |
2 |
1,5 |
3 |
3,5 |
60 |
30 |
16 |
12 |
6 |
8 |
14 |
1,5 |
3 |
2 |
3 |
30 |
60 |
12 |
8 |
4 |
6 |
15 |
2,5 |
2 |
1,5 |
2,5 |
60 |
45 |
15 |
20 |
3 |
8 |
16 |
3,5 |
2 |
2 |
2 |
30 |
45 |
12 |
15 |
6 |
8 |
17 |
4 |
1,5 |
3 |
3 |
45 |
30 |
9 |
12 |
2 |
10 |
18 |
2 |
3 |
1,5 |
1,5 |
45 |
60 |
8 |
14 |
4 |
7 |
19 |
1,5 |
2,5 |
3 |
2 |
30 |
60 |
12 |
16 |
8 |
3 |
20 |
1,5 |
2 |
2 |
5 |
60 |
30 |
7 |
12 |
5 |
8 |
21 |
2,5 |
1,5 |
2 |
1,5 |
30 |
45 |
12 |
10 |
4 |
9 |
22 |
3 |
2 |
2 |
1,5 |
60 |
30 |
11 |
18 |
4 |
7 |
23 |
5 |
3 |
3 |
2 |
30 |
60 |
15 |
12 |
2 |
5 |
24 |
2 |
2 |
3 |
1,5 |
30 |
45 |
8 |
15 |
4 |
8 |
25 |
3 |
2 |
2,5 |
3 |
60 |
30 |
12 |
17 |
6 |
4 |
26 |
4 |
4 |
2 |
2 |
30 |
60 |
17 |
12 |
3 |
5 |
27 |
4 |
1,5 |
2 |
1,5 |
30 |
45 |
6 |
14 |
8 |
5 |
28 |
4 |
2,5 |
1,5 |
2 |
60 |
30 |
8 |
12 |
6 |
4 |
29 |
1,5 |
1,5 |
3 |
2 |
60 |
60 |
17 |
11 |
8 |
6 |
30 |
3,5 |
2 |
3 |
1,5 |
30 |
60 |
11 |
9 |
6 |
8 |
28
1 |
|
|
|
2 |
|
|
|
|
|
|
q |
|
|
Р2 |
β |
|
|
|
Р2 |
M |
|
В |
C |
D |
E |
|
|
|
C'' |
|
|
E |
|
|
q |
|
β |
D |
|
||||
P1 |
|
M |
|
|
|
|||||
α |
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
А |
В |
α |
|
|
|
|
|
|
|
|
C′ |
|
|
|
|||
|
|
|
|
|
|
|
P1 |
|
|
|
3 |
А |
E |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
M |
|
|
|
|
|
|
|
|
|
|
D |
|
|
А |
|
|
|
|
|
|
q |
Р2 |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
q |
|
|
G |
||
|
|
C |
β |
α |
|
|
|
|
||
В |
|
|
|
|
|
β |
E |
|||
α |
|
|
P1 |
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
P1 |
|
|
|
В |
|
C |
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
M |
|
|
q |
|
|
P1 |
|
|
β |
|
P1 |
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
||
α |
В |
|
|
|
В |
|
C |
α |
|
|
C |
D |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Р2 |
|
M |
|
q |
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
E |
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
7 |
M |
Р2 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
E |
|
|
|
|
|
|
|
q |
|
D |
|
β |
q |
|
|
|
β |
|
|
|
|
|
|
C |
|
D |
G |
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
В |
|
M |
|
|
|
В |
|
|
|
α |
|
|
|
||
|
|
|
|
P1 |
|
|
|
|
||
|
P1 |
|
|
А |
|
|
E |
|
||
А |
α |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
Рис.4.1,а |
|
|
|
|
|
|
|
|
|
|
|
29 |
|
|
|
|
|
|
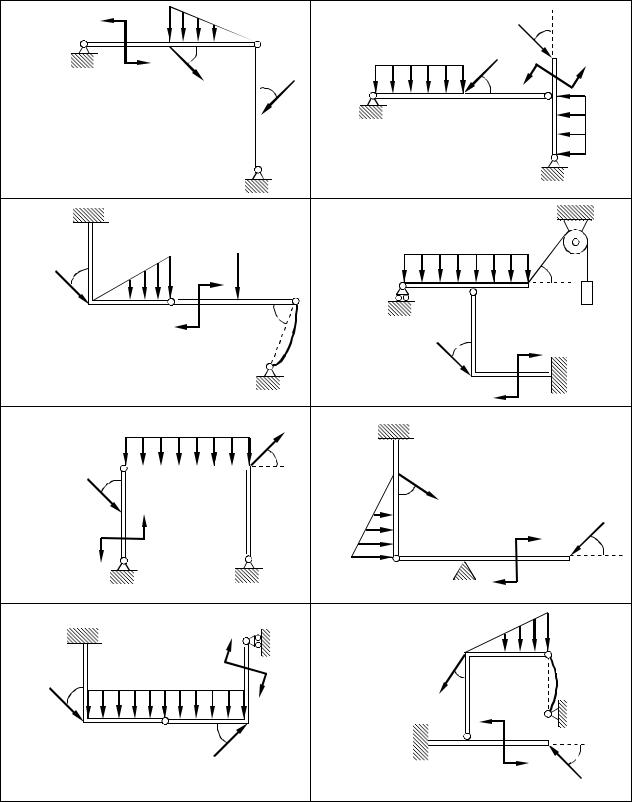
9 |
|
M В |
q |
|
10 |
|
|
|
|
β |
|
|
|
А |
|
|
C |
|
q |
|
Р2 |
|
|
||
|
|
P1 |
α |
|
|
|
|
P1 |
|
D |
|
|
|
|
|
β |
А |
|
|
α |
|
M |
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Р2 |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
В |
|
C |
|
|
|
|
|
|
|
|
|
|
|
q |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P1 |
α |
q |
M |
Р2 |
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
А |
|
|
|
|
|
||
|
|
|
|
|
E |
|
C |
В |
G |
|
||
|
|
|
|
|
|
|
|
|||||
|
В |
C |
|
D |
|
|
|
|
||||
|
|
β |
|
P1 |
α |
|
|
|
|
|||
|
|
|
|
|
|
|
M |
|
|
|
||
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
E |
|
|
13 |
q |
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
Р2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
А |
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
α |
C |
|
D |
|
P1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
P1 |
В |
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
q |
|
|
M |
|
Р2 |
|
|
|
|
|
|
|
|
|
|
|
β |
|||
|
M |
А |
|
E |
|
|
C |
D |
|
|
E |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
15 |
|
|
|
E |
16 |
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
D |
|
|
E |
|
|
|
А |
|
|
|
|
|
|
|
|
|
||
|
|
M |
|
|
|
|
|
|
|
|
|
|
P1 |
|
q |
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
Р2 |
β |
|
|
|
|
||
|
|
|
|
|
|
|
|
F |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
C |
β |
D |
|
|
|
C |
M |
|
|
|
|
|
|
|
Р2 |
|
|
А |
|
|
В |
α |
|
|
|
|
|
|
|
|
|
|
|
|
P1 |
|
|
|
|
|
Рис.4.1,б |
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
