Затухающие колебания

Рис. 1

До сих пор были рассмотрены идеализированные незатухающие колебания, которые возникали в колебательной системе, когда не происходит потери энергии. Однако такие потери всегда есть вследствие наличия сил трения и нагревания проводников в колебательном контуре. Рассмотрим теперь реальные колебательные системы, в которых наблюдается убывание энергии, сообщённой ей. Уравнение колебаний в этом случае записывается в виде:

(14)

где введено обозначение Здесь  представляет собой циклическую частоту затухающих колебаний, а ₀ — собственную циклическую частоту, в отсутствии потерь энергии при колебаниях. График зависимости (14) показан на рис. 1). Из графика видно, что величина  периодически достигает максимума и минимума. В этом смысле процессы, описываемые уравнением (14), можно считать колебательными. Их называют затухающими колебаниями. Наименьший промежуток времени T, через который повторяются максимумы (или минимумы) называют периодом затухающих колебаний. Выражение

(15)

стоящее перед периодической функцией cos(t + ) в формуле (14), рассматривают как амплитуду затухающих колебаний. Она экспоненциально убывает со временем (см. пунктирную кривую на рис. 1). Величина A₀ представляет собой амплитуду колебания в момент времени t = 0, т.е. это начальная амплитуда затухающих колебаний. Величина , от которой зависит убывание амплитуды, называется коэффициентом затухания. Чем больше коэффициент затухания, тем колебания быстрее прекращаются.

Р



ассмотрим характеристики затухающих колебаний. Из выражения (15) теоретически следует, что амплитуда затухающих колебаний становится равной нулю при t  . В связи с этим трудно охарактеризовать быстроту затухания. Поэтому вводят промежуток времени , в течение которого амплитуда затухающих колебаний уменьшается в e раз ( e  2,718  основание натуральных логарифмов), т.е. A(t)/A(t + ) = e. Подставляя (15) в это выражение, получаем: . 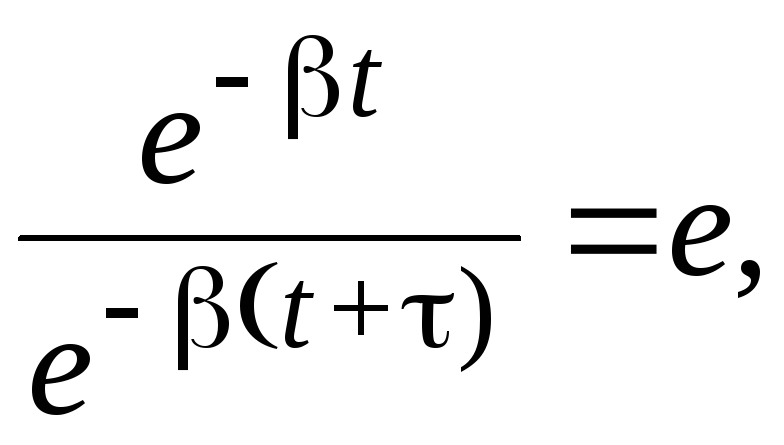Отсюда  = 1 и  = 1/ , т.е. коэффициент затухания обратно пропорционален времени, за которое амплитуда затухающих колебаний уменьшается в e раз.

Н



аряду с коэффициентом затухания используется также понятие логарифмического декремента затухания. Логарифмическим декрементом затухания называют натуральный логарифм от отношения амплитуд затухающих колебаний, соответствующих моментам времени, отличающимся на период колебания, т.е.

(16)

Выясним его физический смысл. Используя выражение (15), из (16), находим: Но  = 1/ и  = N_еT, где N_e — число колебаний за время . Тогда d = T/  = T/(N_eT) = 1/N_e, т.е. логарифмический декремент затухания обратно пропорционален числу колебаний, по истечении которых амплитуда затухающих колебаний уменьшается в e раз.

Вынужденные колебания. Явление резонанса

Вынужденными называют колебания, происходящие под действием периодически изменяющегося воздействия, а сами воздействия называются вынуждающими. Вынужденные колебания происходят с частотой, равной частоте вынуждающих воздействий. В качестве примера рассмотрим вынужденные колебания пружинного маятника. В этом случае на тело, кроме силы упругости и трения, действует вынуждающая сила F, изменяющаяся со временем по закону F = F_m·cos Ωt, где F_m и Ω — амплитуда и циклическая частота колебания. Пусть циклическая частота вынуждающей силы меньше собственной частоты _ пружинного маятника, равной В этом случае маятник совершает гармонические колебания с некоторой амплитудой А_В. Затем начинаем плавно увеличивать частоту вынуждающей силы. При этом амплитуда вынужденных колебаний возрастает. При Ω  _ амплитуда становится максимальной и при дальнейшем увеличении частоты амплитуда вынужденных колебаний снова уменьшается (рис. 3). Аналогичная зависимость амплитуды вынужденных колебаний от частоты наблюдается при электромагнитных колебаниях, происходящих в колебательном контуре. Явление резкого возрастания амплитуды вынужденных колебаний, когда частота вынуждающих воздействий примерно равна собственной частоте колебательной системы, называется резонансом.

Явление резонанса широко используется в технике. Оно может быть как полезным, так и вредным. Так, например, явление электрического резонанса играет полезную роль при настройке радиоприёмника на нужную радиостанцию. Изменяя величины индуктивности и ёмкости, можно добиться того, что собственная частота колебательного контура совпадёт с частотой электромагнитных волн, излучаемых какой-либо радиостанцией. В результате этого в контуре возникнут резонансные колебания данной частоты, амплитуды же колебаний, создаваемых другими станциями, будут малы. Это приводит к настройке радиоприёмника на нужную станцию.

₀

A

0

_

_

₃

₁ > ₂ > ₃

_p1

Р

_p2



ис. 2

С возможностью резонанса приходится считаться при сооружении мостов, производственных зданий, дымовых труб, высотных зданий и т.д. С целью ограничения разрушающего действия резонанса в производственных зданиях под агрегаты (источники вибрации) устанавливаются виброизоляторы. При расчёте высоких и гибких сооружений (дымовые трубы, висячие мосты и т.п.) на ветровую нагрузку предусматривают мероприятия по устройству обтекателей, виброгасителей. Для ограничения передачи колебаний от источника вибраций сооружениям через грунт, в грунте копают глубокие траншеи и наполняют их керамзитом, хорошо поглощающим энергию колебаний.

ВОЛНЫ

Представление о волнах пронизывает нашу жизнь и всю современную технику: волны на море и сейсмические волны в земле, звуковые волны, электромагнитные волны (радиоволны, свет, рентгеновское излучение) и т.д. Волна — это процесс распространения колебаний (возмущения) в пространстве. Геометрическое место точек, до которых дошли колебания, называют фронтом волны. Фронт волны представляет собой поверхность, отделяющую область пространства, в которой происходят колебания, от области, где их ещё нет. Все точки фронта волны колеблются в одинаковых фазах, поскольку колебания в них

начинаются одновременно. Форма фронта волны может быть различной. Простейшими являются сферические и плоские волны, фронт которых соответственно сфера и плоскость Линии, вдоль которых происходит распространение волны, называются лучами. В однородных изотропных средах лучи перпендикулярны к фронту волны. Независимо от фронта волны различают волны продольные и поперечные. В продольной волне колебания происходят вдоль направления распространения; в поперечной — перпендикулярно к направлению распространения. Волны, во всех точках которых совершаются гармонические колебания одинаковой частоты, называются монохроматическими волнами.

7