Лекция №8 колебания

Колебаниями называются процессы, характеризуемые определённой повторяемостью со временем. Можно без преувеличения сказать, что мы живём в мире колебаний и волн. Действительно, живой организм существует благодаря периодическому биению сердца, наши лёгкие колеблются при дыхании. Человек слышит и разговаривает вследствие колебаний его барабанных перепонок и голосовых связок. Световые волны (колебания электрических и магнитных полей) позволяют нам видеть. Другими важными примерами являются переменный ток, электромагнитные колебания в колебательном контуре, радиоволны и т.д. Как видно из приведённых примеров, природа колебаний различна. Однако они сводятся к двум типам — механическим и электромагнитным колебаниям. Оказалось, что, несмотря на различие физической природы колебаний, они описываются одинаковыми математическими уравнениями.

Гармонические колебания

Любая система, способная колебаться или в которой могут происходить колебания, называется колебательной. Колебания, происходящие в колебательной системе, выведенной из состояния равновесия и представленной самой себе, называют свободными колебаниями. Свободные колебания являются затухающими, так как энергия, сообщённая колебательной системе, постоянно убывает. Рассмотрим сначала колебания, полностью пренебрегая причинами, приводящими к убыванию энергии.

1. Гармонические колебания. Гармоническими называют колебания, при которых какая-либо физическая величина, описывающая процесс, изменяется со временем по закону косинуса или синуса:

(t) = A·cos(₀t + ). (1)

Выясним физический смысл постоянных A,  и , входящих в это уравнение.

Константа A называется амплитудой колебания. Амплитуда — это наибольшее значение, которое может принимать колеблющаяся величина. Согласно определению, она всегда положительна. Выражение t + , стоящее под знаком косинуса, называют фазой колебания. Она позволяет рассчитать значение колеблющейся величины s в любой момент времени. Постоянная величина  представляет собой значение фазы в момент времени t = 0 и поэтому называется начальной фазой колебания. Значение начальной фазы зависит от выбора начала отсчёта времени. Величина  получила название циклической частоты, физический смысл которой связан с понятиями периода и частоты колебаний. Периодом незатухающих колебаний называется наименьший промежуток времени, по истечении которого процессы повторяются, или коротко — время одного полного колебания. Число колебаний, совершаемых в единицу времени, называют частотой колебаний. Частота  связана с периодом T колебаний соотношением

(2)

Частота колебаний измеряется в герцах (Гц). Циклическая частота связана с периодом и частотой колебаний соотношением:

(3)

Из этого соотношения следует физический смысл циклической частоты. Она показывает, сколько колебаний совершается за 2 секунд.

2. Пружинный маятник. Пружинный маятник представляет собой тело массой, подвешенное на пружине. Массой пружины и силами трения пренебрегаем.

Рассмотрим превращения энергии, происходящие при колебании такого маятника. Уравнение колебаний пружинного маятника имеет вид:

x(t) = X_mcos(_t + ), (4)

где X_m и ₀ — амплитуда колебания и циклическая частота колебания (см. (1)). Это выражение получается из (1) заменой  на x и A на X_m, учитывая, что Здесь k — коэффициент жёсткости пружины, т — масса тела. Полная механическая энергия W пружинного маятника представляет собой сумму кинетической энергии W_k тела и потенциальной энергии W_p деформированной пружины, т.е.

W = W_k + W_p. (5)

Потенциальная энергия деформированной пружины находится по формуле W_p = kx² /2, где x — величина удлинения пружины, равная отклонению тела от положения равновесия. С учётом (4) получаем:

(6)

так как Кинетическая энергия тела равна W_k = (1/2)m^. Согласно определению скорость тела при движении вдоль координатной оси x равна Тогда скорость тела, совершающего гармонические колебания по закону (4), находим по формуле: Поэтому

(7)

Подставляя (6) и (7) в (5), находим

(8)

поскольку sin²(₀t + ) + cos²(₀t + ) = 1. Таким образом, как следует из (8), полная механическая энергия при свободных гармонических колебаниях не зависит от времени, т.е. остается величиной постоянной. Из соотношений же (6) и (7) вытекает, что потенциальная и кинетическая энергии изменяются со временем пропорционально cos²(₀t + ) и sin²(₀t + ) соответственно. Поэтому, когда одна из них увеличивается, другая уменьшается. Следовательно, в процессе механических колебаний происходит периодический переход потенциальной энергии в кинетическую энергию и обратно. Важно отметить, что энергия колебаний пропорциональна квадрату амплитуды колебаний (см. (8)).

3. Колебательный контур. Колебательным контуром называют электрическую цепь, состоящую из индуктивности и ёмкости. Электрическим сопротивлением контура пренебрегаем.

Рассмотрим теперь электромагнитные колебания в колебательном контуре. Уравнение колебаний заряда q на конденсаторе записывается в виде:

q = q_mcos(₀t + ), (9)

где q_m  амплитуда колебания заряда, ₀  циклическая частота колебаний (см. (1)). Циклическая частота находится по формуле 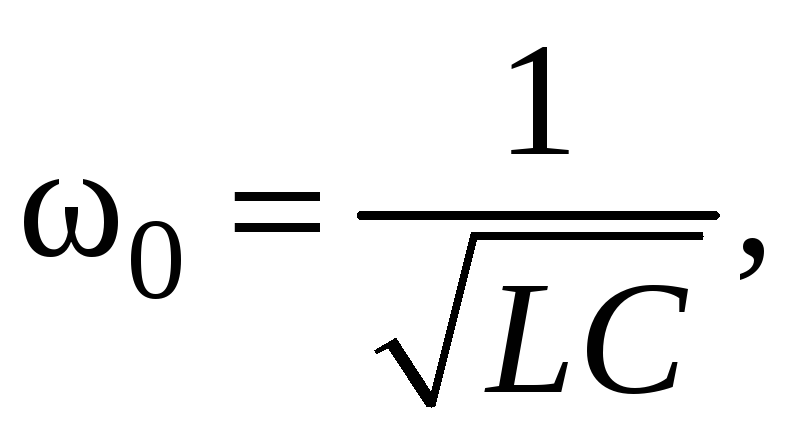где L  индуктивность катушки, С — ёмкость конденсатора.

Энергия W колебательного контура складывается из энергии W_E электрического поля конденсатора и энергии W_B магнитного поля индуктивности, т.е.

W = W_E + W_B. (10)

Но W_E = q²/(2C), где q  величина заряда на конденсаторе, C  ёмкость конденсатора. Учитывая (9), получаем, что

(11)

Энергия магнитного поля находится по формуле W_B = Li²/2. Здесь i  сила тока, проходящего через проводник. Сила тока i в контуре находится дифференцированием соотношения (9) по времени: Тогда Поскольку то

(12)

Подставляя (11) и (12) в (10), находим

(13)

Из соотношений же (11) и (12) следует, что энергии электрического и магнитного полей изменяются со временем пропорционально cos²(₀t + ) и sin²(₀t + ) соответственно. Поэтому, когда одна из них увеличивается, другая уменьшается. Следовательно, в процессе колебаний происходит периодический переход энергии электрического поля в энергию магнитного и обратно, т.е. происходят электромагнитные колебания. Важно отметить, что энергия колебаний также пропорциональна квадрату амплитуды.