6.2. Закон парности касательных напряжений

Вырежем из тела малый элемент (рис.6.3.). Со стороны соседних элементов на него кроме растягивающих напряжений действуют и касательные напряжения (рис.6.4.). Рассмотрим случай, когда растягивающих напряжений нет. Поскольку все тело находится в покое, то и любая его часть, в том числе рассматриваемый малый параллелепипед также находится в покое.

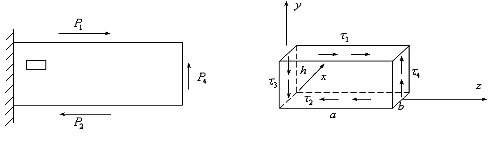
Рис.6.3. Рис.6.4.

Запишем для него уравнения равновесия:

Отсюда вытекает

Закон парности можно сформулировать следующим образом.

Если на грани элемента тела возникает напряжение , то на других трех гранях также возникает такое же напряжение . При этом они сходятся к ребру или расходятся от ребра.

Примечание. Здесь мы рассмотрели случай отсутствия нормальных напряжений. Но этот закон имеет место и при их наличии. Для доказательства этого надо использовать следующие соображения.

Если вертикальные грани имеют бесконечно малый размер hпо сравнению с горизонтальным, то нормальные напряжения не будут давать вклад в первое уравнение равновесия. Аналогично для второго уравнения. Для третьего уравнения можно выбрать осьх, проходящей через центр параллелепипеда.

7. Деформации

Деформирование – это процесс изменения размеров тела.

Деформация – это число, которое характеризует изменение размера тела.

Рассмотрим растяжение бруса. В результате деформирования малый элемент получит абсолютное удлинение на величину.

Определение: Относительным удлинением (синоним - линейная деформация) называется величина:

Правило знаков. Согласно определению понятия «приращение» запишем . Отсюда следует, что если элемент удлиняется, то, а значит, если элемент укорачивается то, и значит.

Примечание: Часто понятия растяжение и удлинениеиспользуют каксинонимы. Однако это не так, понятие растяжение (сжатие) - это силовая характеристика, удлинение (укорочение) – геометрическая. Иногда бывает и так, что элемент сжат, но не деформируется (например, при нагреве элемента, зажатого в жесткой обойме) или даже удлиняется.

Рассмотрим теперь другой вид деформирования элемента тела под действием касательных воздействий.

Под действием прямой параллелепипед превращается в косоугольный.

Угол называетсядеформацией сдвига (синонимы: угол сдвига, сдвиг).

8. Основные предположения и законы, используемые в сопротивлении материалов

8.1. Основные предположения, используемые в сопротивлении материалов

В каждой области науки используются различные свойства тел или полей и наблюдаемые в природе связи между собой различных величин, характеризующих эти свойства, поля, тела. Эти связи называются закономерностями (в разных областях науки и техники они называются по разному – аксиомами, постулатами, гипотезами, законами, правилами, принципами, предположениями).

В сопротивлении материалов используют следующие предположения (хорошо подтверждаемые экспериментально при изучении не слишком малых объектов).

1. Тело считается однородным и сплошным, а не состоящим из молекул и атомов, частиц и т.д. Эта гипотеза позволяет применять дифференциальное и интегральное исчисления, в основе которых лежит метод анализа бесконечно малых величин (следовательно, и бесконечно малых расстояний).

2. В традиционных курсах сопротивления материалов принимается, что свойства тела одинаковы во всех направлениях. Такое тело называется изотропным. Эта гипотеза позволяет уменьшить до минимума число физико-механических характеристик, которые требуется определять из эксперимента. Материалы типа древесины, стеклопластика и т.п. называются анизотропными. У них в разных направлениях механические характеристики разные.

3. Перемещения и деформации тела считаются малыми настолько, что изменением направления действия внешних сил на сечения по мере деформирования тела можно пренебречь. Это позволяет ограничиться знанием только начального положения тела и начального направления внешних воздействий.

4. Принцип Сен-Венана. Он гласит, что напряженное и деформированное состояния тела вдали от области приложения нагрузок мало зависят от истинного (детального) способа приложения этих нагрузок. Это позволяет использовать замену истинных поверхностных нагрузок и объемных сил сосредоточенными силами, погонными силами, моментами. Этот закон проверялся на многих задачах и хорошо подтверждался и экспериментальными исследованиями, и численными расчетами.