9.2.2. Независимость монтажных напряжений от размеров тела

Пусть стержень сделан длиннее на см.

И в этой задаче найти R из уравнений равновесия не удается, поэтому используем геометрическое условие:

.

Аналогично предыдущей задаче получаем отсюда .

Окончательно .

Введем относительную неточность изготовления: .

Тогда

Следствие:

1) Чем больше Е, тем больше монтажное напряжение .

2) Если неточность задавать в относительных величинах , то монтажное напряжениене зависит ни от формы, ни площади сечения, ни от длины, а зависит только от материала, т.е. отЕ, и относительной неточности изготовления.

9.2.3. О температурных и монтажных напряжениях в статически определимых системах

Если произойдет перепад температуры, то в конструкции возникнут удлинения элементов.

Но если нет лишних связей, (то есть задача статически определима), то температурные и монтажные напряжения не возникают.

Например, рассмотрим конструкцию, изготовленную из двух стержней:

Если ее нагреть, то она деформируется. Покажем, что нет напряжений. Сделаем сечение и запишем уравнения равновесия для верхней части:

Получили, что напряжения равны нулю в обоих стержнях.

9.3. Независимость предельной нагрузки от самоуравновешенных начальных напряжений

Рассмотрим статически неопределимую, например, стержневую систему.

Дано:

Найти:

Из рисунка видно, что неограниченная деформация системы начнется тогда, когда потекут оба стержня, то есть:

З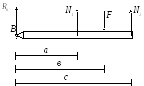апишем уравнения равновесия после рассечения:

.

Подставляем в это уравнения в предельном состоянии:

Следствия:

1. От монтажных и температурных напряжений F* не зависит

Кроме того, можно видеть, что

2. F* не зависит от длин стержней;

3. F* не зависит также от жесткости стержней

9.4. Некоторые особенности деформирования стержней при растяжении и сжатии с учетом силы тяжести

1. Рассмотрим тяжелый стержень (т.е. учитывается собственный вес).

Пусть- плотность материала. Сделаем сечение на расстоянииs от свободного конца (см. рис.9.4.1)

Усилие сжатия на сечение будет:

Тогда

Итак, .

Рис. 9.4.1

Следствие: напряжение, возникающее под действием силы тяжести не зависит от площади и формы сечения, а зависит только от положения сечения и материала.

Рассмотрим теперь задачу вычисления осадки колонны. Вырежем на некотором расстоянии s элемент длины ds.

Рис. 9.4.2

Подсчитаем его укорочение по закону Гука:

.

Суммируя укорочения всех этих элементов, получим полное укорочение стержня. Это будет сумма бесконечно малых величин, то есть интеграл:

.

Итак,

Следствие: деформация стержня под действием собственного веса не зависит от размеров и формы сечения стержня.

9.5. Расчет элементов конструкций с трещинами

Теория расчета тел с трещинами была создана в 1930-ых годах (автором является Гриффитс, первая работа была им опубликована в 1921 г.)

Рассмотрим вывод формулы Гриффитса:

Рис.9.5.1

Пусть в теле есть трещина длины b (рис.9.5.1). Вырежем содержащий её элемент (см. рис.9.5.2).

Рис.9.5.2

Нарисуем растянутые полоски (см. рис.9.5.2). В областях над трещиной и под трещиной материал не может быть нагружен (на см. рис.9.5.2 они представляют собой фигуры типа криволинейных треугольников).

Подсчитаем энергию, накопленную в одной полоске, примыкающей к трещине. Пусть t-толщина пластинки, H-длина полоски. Тогда энергия упругой деформации будет

.

Здесь V - объем полоски. Он равен

Рассмотрим случай, когда трещина начала расти, пусть она увеличилась на ширину полоски . Но после этого в выделенной полоске энергия деформации исчезает, поскольку там нет напряжений. С другой стороны энергия исчезнуть не может - она была потрачена на увеличение трещины на величину, то есть была потрачена на разрыв межмолекулярных связей. Пусть на создание одного квадратного сантиметра трещины требуется энергияС (размерность - кН/см).

Тогда на создание трещины длины см. требуется энергия, равная U=. Согласно закону сохранения энергии должно быть:

W=U

Свяжем Н с шириной трещины. Ясно, что чем больше b, тем больше Н. Это утверждение можно записать в виде:

.

Кроме того, имеет место закон Гука: . Тогда получим:

.

Обозначим: .

Тогда: .

Поскольку трещина начала увеличиваться, это означает, что тело начинает разрушаться. Поскольку напряжение, при котором тело разрушается, называется пределом прочности (обозначается или , или, или), то окончательноформула Гриффитса принимает вид:

Здесь Е – модуль Юнга, а – константа материала, b - длина трещины.