Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования

«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

С.А. Казарин, А.П. Клишин

Практикум по архитектуре компьютера

Учебное пособие

Томск 2009

Томск: Издательство Томского государственного педагогического

университета. 2008. - 97 с. ISBN

Учебное пособие представляет собой базовый курс программирования на языке Assembler. Изложены основные синтаксические конструкции языка Assembler.

2

Введение

3

1.Арифметические основы ЭВМ

1.1Системы счисления

Как известно, системой счисления называется совокупность правил записи чисел c помощью заданного набора специальных знаков – цифр.. Системы счисления подразделяются на позиционные и непозиционные. Как позиционные, так и непозиционные системы счисления используют определенный набор символов- цифр, последовательное сочетание которых образует число. Непозиционные системы счисления появились раньше позиционных. Они характеризуются тем, что в них символы, обозначающие то или иное число, не меняют своего значения в зависимости от местоположения в записи этого числа. Классическим примером такой системы счисления является «римская». В ней для записи чисел используются буквы латинского алфавита. При этом I означает единицу, V- пять, X- десять, L- пятьдесят, C- сто, D- пятьсот, M- тысячу. Для получения количественного эквивалента числа в римской системе счисления необходимо просто просуммировать количественные эквиваленты входящих в него цифр. Исключение из этого правила составляет случай, когда младшая цифра идет перед старшей,- в этом случае нужно не складывать, а вычитать число вхождений этой младшей цифры. К примеру, количественный эквивалент числа 577 в римской системе счисления – это DLXXVII=500+50+10+10+5+1+1=577. Другой пример: CDXXIX=500-100+10+10-1+10=429.

В позиционной системе счисления количество символов в наборе равно основанию системы счисления. Место каждой цифры в числе называется позицией. Номер позиции символа (за вычетом единицы) в числе называется разрядом. Разряд 0 называется младшим разрядом. Каждой цифре соответствует определенный количественный эквивалент. Введем

обозначениезапись А( р) будем обозначать количественный эквивалент числа А, состоящего из n цифр ак (где k=0,…,n-1) в системе счисления с основанием p. Это число можно представить в виде последовательности цифр: А( р) = аn− 1an− 2 ...a1a0 . При этом, конечно, всегда

выполняется неравенство аk<p.

Общее количественное значение числа (количественный эквивалент) не зависит от способа его представления и остается одинаковым во всех системах счисления, различаются только формы представления одного и того же количественного содержания числа.

В общем случае количественный эквивалент некоторого положительного числа А в позиционной системе счисления можно представить выражением:

где: р - основание системы счисления (некоторое целое положительное число); а - цифра данной системы счисления; n - номер старшего разряда числа.

Для получения количественного эквивалента числа в позиционной системе счисления необходимо сложить произведения количественных значений цифр на степени основания, показатели которых равны номерам разрядов (обратите внимание, что нумерация разрядов с нуля).

Двоичная система счисления

Набор цифр для двоичной системы счисления: {0, 1}, основание степени p = 2.

Количественный эквивалент некоторого целого n-значного двоичного числа

Как мы уже отмечали, наличие этой системы счисления обусловлено тем, что компьютер построен на логических схемах, имеющих в своем элементарном виде только два состояния – включено и выключено. Например, рассмотрим двоичное число 10100111.

4

Вычислим количественный эквивалент этого двоичного числа. Согласно формуле (2), это будет величина, равная следующей сумме:

1* 27 + 0* 26 + 1* 25 + 0* 24 + 0* 23 + 1* 22 + 1* 21 + 1* 20.

Сложение и вычитание двоичных чисел (рис. 1) выполняется так же, как и для других позиционных систем счисления, например десятичной. Точно так же выполняются заем и перенос единицы из (в) старший разряд.

Например

Рис. 1. Сложение и вычитание двоичных чисел.

Таблица 1

Шестнадцатеричная система счисления

Данная система счисления имеет следующий набор цифр: {0, 1, 2, …, 9, А, B, C, D, E, F}, основание системы р = 16.

Количественный эквивалент некоторого целого n-значного шестнадцатеричного числа вычисляется согласно формуле (1):

К примеру, количественный эквивалент шестнадцатеричного числа f45ed23c равен: 15 167 + 4 166 + 5 165 + 14 164 + 13 163 + 2 162 + 3 161 + 12 160.

5

Запомнить поначалу эти соотношения сложно, поэтому полезно иметь под руками некоторую справочную информацию. Таблица 2 содержит представления десятичных чисел из диапазона 0-16 в двоичной и шестнадцатеричной системах счисления. Таблицу 2 удобно использовать для взаимного преобразования чисел в рассматриваемых нами трех системах счисления. Шестнадцатеричная система счисления при производстве вычислений несколько сложнее, чем двоичная, в частности, в том, что касается правил переносов в старшие разряды (заемов из старших разрядов). Главное здесь – помнить следующее равенство:

(1+ F = 10)16 .

Эти переходы очень важны при выполнении сложения и вычитания шестнадцатеричных чисел. Пример приведен на рис. 2:

Рис. 2. Сложение и вычитание шестнадцатеричных чисел.

Десятичная система счисления

Это наиболее известная система счисления, так как она постоянно используется нами в повседневной жизни. Данная система счисления имеет следующий набор цифр:

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, основание степени р = 10.

Количественный эквивалент некоторого целого n-значного десятичного числа вычисляется согласно формуле (1)

1.2 Перевод чисел из одной системы счисления в другую

Рассмотрение данных систем счисления само по себе еще только полдела. Для того чтобы в полной мере использовать их по своей практической работе при программировании на ассемблере, необходимо научиться выполнять взаимное преобразование чисел между тремя системами счисления. Этим мы и займемся в дальнейшем. Кроме того, дополнительно будут рассмотрены некоторые особенности микропроцессов Intel при работе с числами со знаком.

Перевод в десятичную систему счисления

Этот тип перевода наиболее прост. Обычно его производят с помощью так называемого алгоритма замещения, суть которого заключается в следующем: сначала в десятичную систему счисления переводится основание степени р, а затем – цифры исходного

6

числа. Результаты подставляются в формулу (1). Полученная сумма и будет искомым результатом. Неявно при обсуждении двоичной и шестнадцатеричной систем счисления мы производили как раз такое преобразование.

котором в качестве делимого (десятичного числа) участвует полученное на шаге 2 частное.

3.Если в результате шага 1 частное q=0, алгоритм прекращается. Выписать остатки в порядке, обратном их получению. Получится двоичный эквивалент исходного числа.

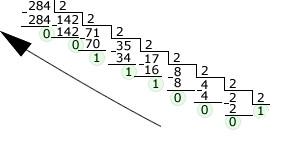
Кпримеру, требуется перевести число 28410 в двоичную систему счисления (Рис. 3):

Рис. 3. Перевод в двоичную систему счисления

Порядок обхода остатков для получения результата показан стрелкой, и результат преобразования равен 1000111002 .

Перевод из шестнадцатеричной системы счисления

Этот переход мы уже обсуждали выше. Суть его заключается в последовательной замене шестнадцатеричных цифр соответствующими двоичными тетрадами согласно табл.

6.2. К примеру, E4D516 → 1110 0100110101012 .

Перевод из десятичной системы счисления

Общая идея такого перевода аналогична рассмотренной выше в алгоритме перевода в двоичную систему счисления из десятичной.

1.Разделить десятичное число А на 16. Запомнить значение частного - q и остаток - а.

2.Если в результат шага 1 частное q ¹ 0, то принять его за новое делимое, записать остаток и вернутся к шагу 1.

3.Если частное q = 0, прекратить работу алгоритма. Выписать остатки в порядке, обратном их получению. Получится шестнадцатеричный эквивалент исходного десятичного числа.

4.В случае, если остаток от деления попадает в диапазон от 10 до 15, в результат записывается шестнадцатеричный цифра (A, B, C, D, E или F), а не полученное в остатке десятичное число.

Перевод из двоичной системы счисления

Идея алгоритма аналогична идее перевода из двоичной системы счисления в шестнадцатеричную. Суть в том, что двоичное число разбивается на тетрады, начиная с младшего разряда. Далее каждая тетрада приводится к соответствующему шестнадцатеричному числу согласно табл. 2.

К примеру, требуется перевести число

7

111001011010111101011000110110001111010101011012 в шестнадцатеричную систему счисления.

Разобьем его на тетрады:

0111 0010 1101 0111 1010 1100 0110 1100 0111 1010 1010 1101.

По тетрадам приводим последовательности нулей и единиц к шестнадцатеричному представлению:

7 2 d 7 a c 6 c 7 a a d.

В итоге мы получили результат преобразования: 111001011010111101011000110110001111010101011012 → 72d7ac6c7aad16 .

Перевод дробных чисел

Учащийся должен уметь выполнять перевод в различные системы счисления не только целых чисел, но дробных. Особенно это важно при программировании алгоритмов, использующих операции с плавающей точкой. Без владения в полной мере знаниями о том, как представляются дробные числа в памяти компьютера и в регистрах сопроцессора, вам вряд ли удастся овладеть программированием на ассемблере в полной мере. Давайте разберемся с наиболее часто используемыми на практике способами перевода дробных чисел. Для этого формулу (1) преобразуем к следующему виду:

для вас труда не составит. Для вычисления остальной части выражения удобно использовать табл. 3.

Таблица 6. Значения отрицательных степеней по основанию числа 2

Далее вы сами можете продолжить табл.3 значениями отрицательных степеней по основанию числа 2.

Упражнение. Посчитайте результат перевода значения 110100,010010112 в десятичное представление.

Пример 2. Перевести в десятичное представление дробь в шестнадцатеричной системе счисления 1df2,a1e416.

Вновь используем формулу (3) и получим:

1dt2,ale416 = 1 163 + 13 162 + 15 21 + 2 160 + 10 16− 1 + 1 16− 2 + 14 16− 3 + 4 16− 4.

8

Для удобства вычисления дробной части приведем значения отрицательных степеней числа 16 табл. 4.

Таблица 4. Значения отрицательных степеней по основанию числа 16

Перевод из двоичной системы счисления в шестнадцатеричную систему и обратно выполняется, как обычно, на основе тетрад и трудности вызывать не должен.

Рассмотрим теперь проблему представления десятичных дробей в двоичной и шестнадцатеричной системах счисления.

Общий алгоритм перевода десятичной дроби в другую систему счисления можно представить следующей последовательности шагов:

1.Выделить целую часть десятичной дроби и выполнить ее перевод в выбранную систему счисления по алгоритмам, рассмотренным выше.

2.Выделить дробную часть и умножить ее на основание выбранной новой системы счисления.

3.В полученной после умножения дробной части десятичной дроби выделить целую часть и принять ее в качестве значения первого после запятой разряда числа в новой системе счисления.

4.Если дробная часть значения, полученного после умножения, равна нулю, то прекратить процесс перевода. Процесс перевода можно прекратить также в случае, если достигнута необходимая точность вычисления. В противном случае перейти к шагу 3.

Пример 3. Перевести в двоичную систему счисления десятичную дробь 108,40610. Переведем целую часть десятичной дроби 248,568 в двоичную систему счисления (рис. 5).

Рис. 5. Перевод целой части числа 248,568 в двоичную систему счисления

Переведем дробную часть десятичного числа 248,568 по алгоритму, приведенному выше (рис. 6).

9

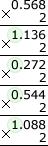
Рис. 6. Перевод дробной части числа 248,568 в двоичную систему счисления

Результат перевода следующий: 248,568 = 100011100,1001.

При переводе дробного числа из десятичной системы счисления в шестнадцатеричную целесообразно предварительно перевести число в двоичную систему. Затем двоичное представление разбить на тетрады отдельно до запятой и после запятой. Разбиение на тетрады двоичных разрядов целой части производят от запятой в сторону старших разрядов. Неполную старшую тетраду дополняют слева ведущими нулями. Разряды дробной части, напротив, разбивают на тетрады от запятой вправо к младшим разрядам. Если последняя тетрада неполная, то ее дополняют справа нулями.

Перевод в десятичную можно осуществить аналогично переводу из двоичной СС, только умножать нужно уже не на степени 2, а на степени 16.

Числа со знаком

До сих пор предполагалось, что числа положительные. А как представляются в компьютере числа со знаком? Кодирование осуществляется за счет введения дополнительного бита знака, обычно расположенного перед битом старшего разряда.

Положительные целые со знаком – кодируются значением 0, в бите знака. Отрицательные целые со знаком - 1. Отличительным признаком числа со знаком

является особая трактовка старшего бита поля, представляющего число. В качестве поля могут выступать байт, слово или двойное слово. Естественно, что физически этот бит ничем не отличается от других,- все зависит от команды, работающей с данным полем. Если в ее алгоритме заложена работа с целыми числами со знаком, то она будет по-особому трактовать старший бит поля. В случае если бит равен 0, число считается положительным и его значение вычисляется по правилам, которые мы рассмотрели выше. В случаи если этот бит равен 1, число считается отрицательным и предполагается, что оно записано в так называемом дополнительном коде. Разберемся в том, что он собой представляет.

Дополнительный код некоторого отрицательного числа представляет собой результат инвертирования (замены 1 на 0 и наоборот) каждого бита двоичного числа, равного по модулю исходного отрицательного числа плюс единица. К примеру, рассмотрим десятичное число – 18510. Модуль данного числа в двоичном представлении равен (10111001)2. Сначала нужно дополнить это значение слева нулями до нужной размерности – байта, слова и т. д. В нашем случае дополнить нужно до слова, так как диапазон представления знаковых чисел в байте составляет -128…127. Следующее действие – получить двоичное дополнение. Для этого все разряды двоичного числа нужно инвертировать:

(0000000010111001)2 → (1111111101000110)2. Теперь прибавляем единицу:

(111111101000110)2+(0000000000000001)2 = (1111111101000111)2.

Результат преобразования равен (1111111101000111)2. Именно так и представляется число – 18510 в компьютере.

При работе с числами со знаком от вас наверняка потребуется умение выполнять обратное действие – имея двоичное дополнение числа, определить значение его модуля. Для этого необходимо выполнить два действия:

10

1.Выполнить инвертирование битов двоичного дополнения.

2.К полученному двоичному числу прибавить двоичную единицу.

Кпримеру, определим модуль двоичного представления числа – 18510

=(1111111101000111)2 (1111111101000111)2 → инвертируем биты → (0000000010111000)2. Добавляем двоичную единицу:

(0000000010111000)2 + (0000000000000001)2 = (0000000010111001)2 = |-185|.

Теперь вам должно быть понятно, откуда появилась разница в диапазонах значений для чисел со знаком и без знака простых типов данных.

2. Формы представления данных в ЭВМ

ВЭВМ используются следующие формы представления данных.

·Числа с фиксированной точкой (запятой)

·Числа с плавающей точкой

·Десятичные числа

·Символьные данные

2.1. Формы представления чисел в ЭВМ

Обычно числа в машинах представляются в одной из двух форм: с фиксированной запятой или с плавающей запятой.

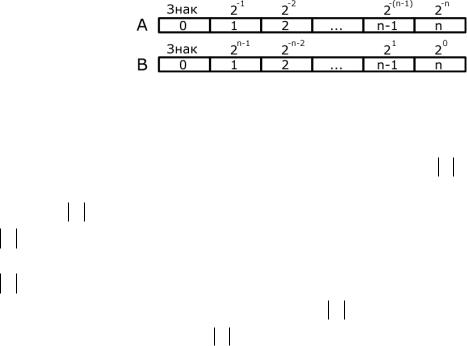
Представление чисел с фиксированной запятой. В разрядной сетке (ячейке) машины число записывается последовательностью изображающих его двоичных цифр. Количество разрядов, отведенное для записи дробной и целой частей чисел, строго

фиксировано a0 a1a2 a3 ...an . Это позволяет запятую в изображении числа опускать. Для

изображения знака числа обычно отводится самый левый разряд ячейки a0 , причем "плюс"

кодируется двоичной цифрой 0, а "минус" – 1.

На практике при представлении чисел с фиксированной запятой запятая "закрепляется" либо перед самым левым разрядом числа, либо после самого правого. В первом случае все числа по модулю меньше единицы, а во втором случае все числа целые.

A)Запятая фиксирована перед первым разрядом (после a0 )

B)Запятая фиксирована после n-го разряда ( an )

Очевидно, что в случае а) в разрядной сетке могут быть записаны числа от - (1- 2− n ) до 2− n и от 2− n до + (1- 2− n ) , а так же и нуль. Числа N, для которых N < 2− n не могут быть представлены в такой форме и принимаются равными нулю. Не могут быть представлены и числа такие, что N ³ 1.

N £ 2n - 1

При представлении, соответствующем б),

N £ 1- 2− n

кроме нуля, могут быть записаны числа такие, что 1 £ N < 2− n .

Все числа из диапазона 0 < N < 1 не могут быть представлены в такой форме и принимаются равными нулю.

11

Очевидно, что при выполнении арифметических операций над числами с фиксированной запятой может произойти переполнение разрядной сетки, то есть превышение значения результата верхней границы - 1 в случае а) и 2n в случае б).

двоичных со знаком принято называть прямым кодом числа.

Всовременных универсальных ЭВМ используется представление чисел с фиксированной запятой в форме б), то есть предназначенных для выполнения операций над целыми числами.

Впамяти ЭВМ числа с фиксированной точкой могут хранятся в трех форматах

1)полуслово – 16 бит, 2 байт,

2)слово – 32 бита,4 байта,

3)двойного слово – 64 бита, 8 байт.

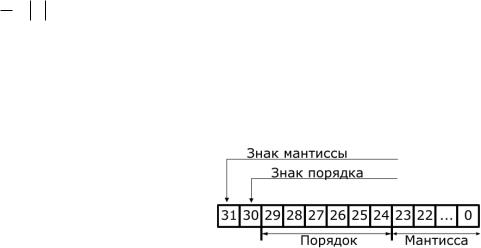
Представление чисел в форме с плавающей запятой.

При форме представления с плавающей запятой число N считают приведенным к

виду:

где m - число с запятой, фиксированной после определенного разряда, называемое мантиссой, n - целое число, называемое порядком, а Р – основание системы счисления.

Запятую в мантиссах, как правило, фиксируют перед старшим (цифровым) разрядом, то есть в качестве мантисс берут правильные дроби. Это, связано с удобством умножения мантисс (их произведение будет при этом также правильной дробью).

Если в записи (1) старшая цифра мантиссы отлична от нуля, то число N называют нормализованным (в противном случае - ненормализованным). При запятой, фиксированной перед старшим разрядом мантиссы, нормализованными являются числа, для которых

P1 £ m < 1.

Пример. Десятичное число 25,2 в форме с плавающей запятой (при запятой мантиссы, фиксированной перед старшим разрядом) может иметь любой из видов 0,252*102; 0,0252* 103; 0,00252*104 и т.д. Нормализованной является только запись 0,252* 102, а все остальные являются ненормализованными.

Ниже изображено возможное представление нормализованных чисел с плавающей запятой в 32-х разрядной сетке ЭВМ.

При обработке в ЭВМ чисел с плавающей запятой также возможно переполнение разрядной сетки, которое заключается в том, что в результате какой-либо операции возникает число, имеющее порядок с большей разрядностью, чем допустимая при представлении порядка в машине. Кроме того, в машине возможно появление машинных нулей, т.е. нормализованных чисел, отличных от нуля, но имеющих порядок, меньший самого малого порядка, представимого в разрядной сетке. Обычно машинные нули записываются в виде нулевой мантиссы и нулевого порядка.

12

Если количество разрядов мантиссы больше количества, выделенного для ее представления в разрядной сетке ЭВМ, избыточные младшие разряды отбрасываются, возможно, с округлением последнего из оставшихся.

Диапазон нормализованных двоичных чисел с плавающей запятой, представленных в разрядной сетке ЭМВ, если запятые в мантиссах фиксированы перед старшими разрядами, оценивается неравенствами:

2− 2S £ N £ (1 - 2− k ) × 22S − 1

где N - исходное число, к - количество цифровых разрядов мантиссы, s - количество цифровых разрядов порядка.

В памяти ЭВМ числа с плавающей точкой хранятся в двух форматах:

1)слово – 32 бита, 4 байта.

2)двойного слово – 64 бита, 8 байт.

2. Сложение и вычитание в ЭВМ

Операции над числами с фиксированной запятой. Операция вычитания в машине реализуется достаточно сложно, так как при этом часто возникает необходимость "занимания" единиц в соседнем старшем разряде. Если же в соседнем старшем разряде этого сделать нельзя, необходим заем в более старшем разряде и т.д. Если же уменьшаемое меньше вычитаемого, этот процесс будет продолжаться до самого старшего разряда, а затем нужно вычитание делать заново, поменяв знак разности и вычитаемое и уменьшаемое местами.

Для упрощения операции вычитания и сведения ее к операции сложения, так чтобы операция алгебраического сложения в машине выполнялась единообразно, применяют специальные способы представления отрицательных чисел.

Прямой код. Рассмотрим двоичное число N = ± 0,a1 ,a2 ,..., an

В разрядной сетке число N представляется (кодируется) следующим образом:

Аналогичным образом кодируются и числа, модуль которых не меньше единицы. Пример. Записать двоичные числа в прямом коде:

Дополнительный код. Из равенства х - у = х + (Р - у) - Р следует, что операцию вычитания у из х можно заменить операцией сложения Р-у и х с последующим вычитанием из результата величины Р (где Р - основание степени).

Введем запись:

Представление чисел в соответствии с записью [И]д называется дополнительным кодом числа N.

13

Обратный код. Операцию вычитания можно заменить операцией сложения и на

осно

ве соотношения х-у=х+(Р-Р-n -у)-Р+Р-n. Код, определенный с помощью соотношения:

Называется обратным кодом числа N.

Отметим, что при Р=2 для получения обратного кода отрицательного числа в знаковый разряд нужно записать единицу, а каждую цифру в записи числа заменить на ее дополнение до Р-1, то есть единицу заменить на нуль, а нуль на единицу.

Пример. Записать двоичные Числа в обратном коде:

Из приведенных выше соотношений следует, что

[N ]Д = NОБР + P− n ,

то есть отличие в записи дополнительного и обратного кодов отрицательного числа заключается в последнем разряде. Если в последнем (n-м) разряде в дополнительном коде записывается (Р-аn), то в обратом (Р-1- аn). Отсюда следует, что для получения дополнительного кода отрицательного числа нужно к его обратному коду прибавить единицу.

Пример. Записать двоичные числа в дополнительном коде:

обратном и дополнительном кодах совпадают. В прямом и обратном коде нуль имеет два представления - "положительный" и "отрицательный" нуль. В дополнительном коде нуль имеет только одно, "положительное" представление.

Алгебраическое сложение. Рассмотрим сначала использование обратного кода для алгебраического сложения n-разрядных двоичных чисел R и Q, когда оба они или, одно из них отрицательно. Будем считать, что модуль их алгебраической суммы меньше единицы и единица переноса из разряда знака прибавляется к младшему разряду получившейся суммы.

Пусть R<0 и Q<0. Считаем, что -1<R+Q<1. Тогда можно записать

Таким образом, сложение с переносом единицы знакового разряда (циклическим переносом) двух отрицательных чисел в обратном коде дает обратный код их алгебраической суммы.

Пусть R>0 и Q<0. Можно записать: [R]ПР + [Q]ОБР = R + 2 + Q - 2− n

Если (R+Q)>0, то 2+(R+Q)>2 и возникает перенос из разряда знака. В этом случае

имеем:

[R]ПР + [Q]ОБР = R + Q - 2− n + 2− n = [R + Q]ПР

Если (R+Q)<0, то 2 + (R+Q) < 2, и переноса не возникает, получаем:

[R]ПР + [Q]ОБР = 2 + (R + Q) - 2− n = [R + Q]ОБР

14

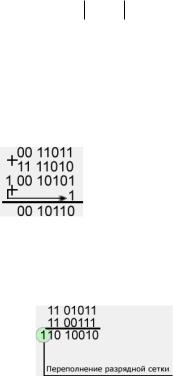
Таким образом, сложение чисел с использованием обратных кодов с циклическим переносом приводит к получению алгебраической суммы в прямом коде, если сумма положительна, и в обратном коде, если сумма отрицательна.

Аналогично можно показать, что при использовании дополнительных кодов алгебраическое сложение их, включая разряды знаков, которые рассматриваются как разряды целых единиц, дает, если единица переноса из разряда знака отбрасывается, следующий результат: если алгебраическая сумма положительна, то результат получается в прямом коде, и в дополнительном коде, если она отрицательна.

Таким образом, используя обратный и дополнительный коды, операцию алгебраического сложения можно свести к арифметическому сложению кодов чисел, которое распространяется и на разряды знаков, которые рассматриваются как разряды целой части числа.

Модифицированный код. Таким образом, применение обратного и дополнительного кодов дает возможность операцию алгебраического сложения свести к операции арифметического сложения. Выше рассмотрен случай, когда модуль полученной суммы меньше единицы. В общем случае при сложении двух чисел, модуль которых меньше единицы, модуль суммы может оказаться больше или равен единице (переполнение разрядной сетки мантиссы).

Для обнаружения такого переполнения, учитывая, что модуль суммы двух таких чисел всегда меньше двух, используют один дополнительный разряд. Код (прямой, дополнительный, обратный), в котором имеется такой дополнительный разряд, называется модифицированным. В модифицированных кодах – дополнительный разряд используется для дублирования знака числа, то есть знак «плюс» обозначается 00, а "минус" - 11. Правила переноса из разрядов знака остаются прежними в зависимости от того, в каком коде (обратном или дополнительном) представлены числа. На переполнение же разрядной сетки,

то есть ситуацию, когда модуль суммы 1 ≤ R + Q < 2 указывает несовпадение цифр в

знаковых разрядах. В этом случае комбинации 01 соответствует положительное, а 10 - отрицательное число.

Пример. Сложить двоичные числа R=-0,11011 и Q=-0,00101. Прямой модифицированный код [R]ПРМ = 00 11011 Обратный модифицированный код [R]ОБРМ = 11 11010

Пример. Сложить двоичные числа R=-0.10101 и Q=-0,11001. Дополнительный модифицированный код [R]ДМ = 11 01010

Дополнительный модифицированный код [Q]ДМ = 11 00111

[R + Q]ДМ = 1010010

Операции над числами с плавающей запятой. Пусть имеется два нормализованных числа: X = m1Pn и Y = m2 Pk

15

Пусть сначала оба числа не отрицательны. Тогда, в соответствии с приведенными формулами, в машине выполняются следующие действия:

1)Происходит выравнивание порядков чисел, причем порядок меньшего числа приводится к порядку большего числа, то есть порядок меньшего числа принимается равным порядку большего числа.

2)Для того, чтобы исходное число не изменило своего значения, мантисса меньшегочисла сдвигается на соответствующее число разрядов вправо (уменьшается в соответствующее число раз).

3)Происходит сложение или вычитание мантисс, в результате чего получается мантисса результата. Порядок результата в соответствии с произведенным выравниванием порядков принимается равным порядку большего числа.

4)Полученный результат округляется и, если нужно, нормализуется. Округление результата может быть реализовано несколькими способами. Например, один из них заключается в том, что предварительный результат вычисляется с количеством разрядов, большим, чем разрядная сетка чисел, над которыми производится операция. Если используется двоичный код, то достаточно одного лишнего разряда. В этом случае округление заключается в прибавлении к этому дополнительному младшему разряду предварительного результата единицы. 'Если в дополнительном разряде был получен нуль, это не вызовет переноса единицы в основные разряды. Если же в дополнительном разряде записана единица, то предварительный результат будет увеличен на единицу младшего разряда. После проведения, этих действий дополнительный разряд отбрасывается.

Таким образом, при выполнении операций сложения и вычитания возникает проблема выравнивания порядков чисел, то есть прежде всего должен быть проведен анализ знаков и величин порядков.

Для упрощения операций над порядками в ЭВМ порядок всех чисел увеличивается на одно и то же число так, чтобы порядок наименьшего числа, представимого в машине, был

бы неотрицательным, то есть машинный порядок всех чисел nm удовлетворяет условию

Таким образом, порядки всех чисел в машине становятся положительными, и анализ знака порядка теряет смысл.

Отметим, что при представлении чисел с плавающей запятой отдельно кодируются мантисса и порядок. При этом возможно представление мантисс и порядков чисел в одном и том же или разном кодах. Например, порядок числа может быть представлен в прямом, а мантисса - в дополнительном кодах и т.п.

Таким образом, в общем случае сложение и вычитание чисел с плавающей запятой состоит из следующих этапов:

-сравнивание порядков чисел;

-выравнивание порядков чисел;

-перевод мантисс слагаемых в обратный или дополнительный модифицированные коды;

-сложение мантисс в прямом, обратном или дополнительном модифицированных кодах;

-исправление нормализации вправо или влево;

-перевод мантиссы результата в прямой код;

16

-выдача результата с учетом порядка.

Представление десятичных чисел в ЭВМ.

При представлении информации в виде десятичных многоразрядных чисел каждая десятичная цифра заменяется двоично-десятичным кодом.

(Ц)10=(Ц)2(Ц)2(Ц)2(Ц)2 Для ускорения обмена информацией, экономией памяти и удобства операций над

десятичными числами предусматриваются специальные форматы их представления: зонный, (распакованный) и упакованный.

Зонный формат используется в операциях ввода-вывода десятичных данных, упакованный формат – для выполнения арифметических операций. Для этого в ЭВМ имеются специальные команды упаковки и распаковки десятичных чисел.

Зонный формат.

Каждая цифра занимает один байт, причем в левую тетраду (зону) записывается код 1111(2)=F(16). В одном из крайних байтов зоны отведены для представления знака числа.

Например, в ЕС ЭВМ для представления знака “+” выбран код 1100(2)=С(16), для представления знака “-“ – код 1101(2)=D(16). Код знака записывается в зону последнего байта

(Рис. 1). Пример: число – (-6285) в зонном формате будет представлено в виде: F6 F2 F8 D5.

Зона Цифра Зона Цифра ... Зона Цифра

Рис. 1. Зонный формат (распакованный).

Рис. 2. Упакованный формат.

Рис. 3. Упакованный формат. Мини ЭВМ.

Вупакованном формате каждый байт содержит код двух десятичных цифр. Правая тетрада последнего байта используется для кода знака числа (Рис. 2). Десятичное число должно занимать целое число байтов. Если это условие не выполняется, то левая тетрада левого байта заполняется нулями. Пример. Код десятичного числа -6285 в упакованном формате имеет вид 06285D. Для представления десятичных чисел в памяти используется прямой код.

Вмалых ЭВМ десятичные числа в упакованном формате (Рис. 3) представляются дополнительным кодом, причем знаку плюс соответствует код 0000, а знаку минус – код

1001(2). Пример. Код числа -6285 в упакованном формате для малых ЭВМ имеет вид 9.3715 (Перевести в обратный код).

17

ЦИФРОВОЕ ПРЕДСТАВЛЕНИЕ ТЕКСТОВОЙ ИНФОРМАЦИИ

Представление текстовой информации в электронных публикациях осуществляется с помощью стандартов кодирования текста (символов) и текстовых форматов. На данный момент их перечень весьма ограничен. В качестве стандартов кодирования символов используются ASCII, ANSI, UNICODE. Из множества известных форматов в электронных изданиях нашел применение формат PDF, предложенный фирмой Adobe Systems для программных средств создания и просмотра электронных изданий Adobe Acrobat. Стандартом де-факто является формат RTF, предложенный фирмой Microsoft для организации обмена текстовой и графической информацией. Однако его применение в электронных изданиях весьма ограничено.

3.1. Стандарты кодирования символов ASCII, ANSI, КОИ-8 и UNICODE

Представление символов в электронных изданиях базируется на таблицах кодов, в которых каждому из отображаемых на экране символов соответствует код от 0 до 255. Первые 127 кодовых комбинаций используются для латинских букв и цифр, знаков пунктуации и т.д. и, как правило, строятся по единому принципу.

Стандарт представления символов ASCII - это 7-битовое описание кода символа. Поскольку в персональных компьютерах используются байты, состоящие из 8 бит, производители компьютеров часто определяют наборы символов, использующие 256 кодов вместо 128 кодов ASCII. В результате получается "расширенный набор символов" (extended character set), который включает в себя набор символов ASCII и до 128 других символов.

В начале 80-х годов производители IBM PC решили расширить набор символов ASCII так, как показано на рис. 3.1. Коды от 20h до 7Ah - это выводимые на дисплей символы из набора символов ASCII. Оставшиеся символы являются нестандартными или, по крайней мере, на тот момент являлись нестандартными .

1.1.1. Кодирование символов

Буквы алфавита, цифры, скобки, запятые и т.д. нужно кодировать цепочками нулей и единиц, так же как и целые числа, как и любую другую информацию. Нужно только условиться о том, какому символу какая цепочка соответствует. Тогда, по коду буквы A на экране дисплея будет нарисована картинка с изображением буквы A, принтер напечатает изображение буквы A. Международным стандартом кодирования символов стал ASCII (произносится "аски") — American Standard Code for Information Interchange — Американский стандартный код для обмена информацией.

Код символа занимает один байт, т.е. всего можно закодировать 256 символов. ASCII фиксирует только коды от 0 до 127 (0h – 7Fh). Коды 128 – 255 (80h – 0FFh) составляют расширение ASCII, которое не стандартизировано. В России в качестве расширения принята так называемая альтернативная кодировка.

Изучим таблицу кодов (её нижнюю половину) подробнее (табл.1.4). Сначала объясним, как она построена. Шапка таблицы соответствует единицам, а боковик — десяткам (в 16ричной системе счисления). Поэтому код буквы z, например, есть 70h + 0Ah = 7Ah.

Таблица 1.4

18

Символы делятся на два больших класса: графические (для символа имеется изображение) и управляющие (им соответствуют специальные сигналы и функции устройств).

Графические символы. Эти символы разбиваются на несколько классов.

Прописные латинские буквы. A – 41h, B – 42h, C – 43h,…, Z – 5Ah. Код следующей по алфавиту буквы возрастает на единицу. Это позволяет организовать в программах лексикографическое упорядочение цепочек символов: сравниваются коды символов на "больше-меньше".

Строчные латинские буквы. a – 61h, b – 62h, c – 63h, ... z – 7Ah. Код строчной буквы получается прибавлением 20h к коду прописной буквы.

Цифры. 0 – 30h, 1 – 31h, ... , 9 – 39h. Чтобы получить код цифры надо прибавить к цифре код цифры 0, т.е. 30h.

Символы пунктуации: ^(){} и т.д. Отметим код пробела 20h. Начинающие ошибочно предполагают, что пробел кодируется нулем.

Управляющие символы. Эти символы при вводе с клавиатуры или при передаче периферийному устройству вызывают выполнение определенной функции или посылку сигнала. Коды этих символов 0 – 1Fh и FFh. Они имеют специальные обозначения. Приведём только два управляющих символа.

LF — line feed — перевод строки (код 0Ah) — перемещает курсор на экране терминала вниз на одну строку.

CR — carriage return — возврат каретки (код 0Dh) — перемещает курсор на экране терминала к началу текущей строки. В большинстве терминалов клавиша Enter вызывает и возврат каретки (CR), и перевод строки (LF).

Задание A1.

1.Преобразовать десятичное число в 16-ричную и двоичную системы счисления (пример 4020).

2.В байте записано число. Перевести его в десятичную систему счисления, рассматривая как беззнаковое и как знаковое. Какому символу кодовой таблицы соотвествует число. Ответ — с обоснованием — должен быть представлен в виде таблицы

54h

D6h

Расширеный набор символов IBM

Этот набор символов закодирован в миллионах микросхем ПЗУ в видеоадаптерах, принтерах и микросхемах BIOS. Он был растиражирован в аппаратуре многочисленных производителей IBM-ориентированных компьютеров и периферии. Для множества программ, работающих в текстовом режиме и написанных не для MS Windows, требуется

19

этот расширенный набор символов, поскольку в них для вывода информации на экран используются символы псевдографики - символы блоков и линий (коды от B0h до D0h).

Рис. 3.1. Расширенный набор символов IBM (упорядочен по возрастанию значений кода символов)

Известно несколько вариантов кодирования символов IBM, которые называются "кодовые страницы" (code pages). Вариант, используемый в Соединенных Штатах Америки и большинстве европейских стран, называется Code Page 437. В системах, распространенных в Норвегии, Дании, Португалии и некоторых других странах Европы, используются другие специальные кодовые страницы, в которых содержится большее количество специальных символов, необходимых для языков этих стран. В последнее время некоторые страны начали применять кодовую страницу Code Page 850, в которой содержится меньшее количество псевдографических символов. За счет этого введены дополнительные символы, знаки ударения и другие специальные символы.

Расширенный набор символов ANSI (ANSI character set)

Расширенный набор символов, который Windows и программы для Windows в большинстве случаев используют, называется набор символов ANSI (ANSI character set), фактически он является международным стандартом ISO. Кодовая таблица стандарта ANSI представлена на рис. 3.2.

20

Рис. 3.2. Набор символов ANSI (упорядочен по возрастанию значения кода)

В нашей стране кодовые комбинации начиная со 128 используются для кодирования символов кириллицы, математических символов и другой информации. Причем для каждой платформы используется свое расположение символов в кодовой таблице. Так, известны кодировки Windows, Mac, DOS-OS/2, ISO (Dec) и КОИ-8. Поэтому приходится осуществлять перекодировки символов кириллицы электронных изданий в зависимости от используемой платформы.

Альтернативная кодировка

Справедливости ради следует отметить, что существуют нормативы: "Основная кодировка ГОСТа", "Альтернативная кодировка ГОСТа" и кодировка КОИ-8. В последнем случае символы кириллицы имеют коды: А - Я - 224 - 254 (не в алфавитном порядке); а - я - 192 - 223 (не в алфавитном порядке).

По мнению специалистов, "Альтернативная кодировка ГОСТа" использует под кодировки символов кириллицы позиции, где в кодировке IBM расположены относительно редко используемые символы национальных алфавитов, греческие буквы и некоторые математические символы.

На рис. 3.3 приведена таблица кодировки символов кириллицы для "Альтернативной кодировки ГОСТа" (Alt), "Основной кодировки ГОСТа" (Mai), кодировки MIC и КОИ-8.

21

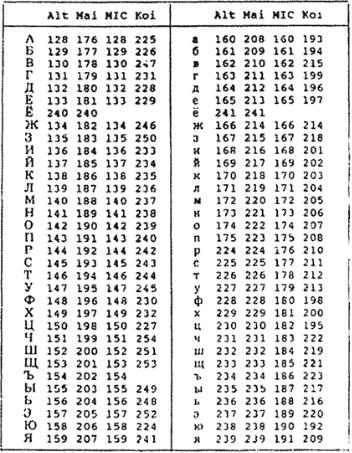
Рис. 3.3.Кодировки символов кириллицы

Стандарт кодировки символов UNICODE

Стандарт UNICODE был предложен некоммерческой организацией Unicode Consortium, образованной в 1991 г. Для представления каждого символа в этом стандарте используются два байта: один байт для кодирования символа, другой для кодирования признака. Тем самым обеспечивается информационная совместимость данного способа кодирования со стандартом ASCII.

Двухбайтовое описание кодов символов позволяет закодировать очень большое число символов из различных письменностей. Так, в документах Unicode могут соседствовать русские, латинские, греческие буквы, китайские иероглифы и математические символы.

Кодовое пространство Unicode разделено на несколько областей. Область с кодами от 0000 до 007F содержит символы набора Latin 1 (младшие байты соответствуют кодировке ISO 8859-1). Далее идут области, в которых расположены знаки различных письменностей, а также знаки пунктуации и технические символы. Часть кодов зарезервирована для использования в будущем (29000). 6000 кодовых комбинаций оставлено программистам.

Символам кириллицы выделены коды в диапазоне от 0400 до 0451.

Ниже приведена основополагающая таблица использования кодового пространства Unicode (табл. 3.1).

Таблица 3.1

22

Вдокументах Unicode используются различные шрифты. Как правило, файл шрифта Unicode содержит начертания не для всех символов, определенных в стандарте, а лишь для символов из некоторых областей.

Некоторые программы, например ядро Windows NT, ее графический интерфейс (GDI)

ифайловая система (NTFS), реализованы с использованием Unicode. Программы, запущенные в среде NT, могут работать также с однобайтовыми символами, кодировка которых в этом случае соответствует установленной по умолчанию кодовой странице ANSI (для России-Windows Cyrillic).

Перед вызовом некоторых функций программного интерфейса NT программы, работающие с кодовой страницей ANSI, преобразуют однобайтовые символы в Unicode. Чтобы преобразование выполнялось без ошибок, обычно указывается страна в приложении Regional Settings. Такой же подход используется для корректной работы с национальными символами программ в среде MS-DOS.

Вотличие от Windows NT ядро и графический интерфейс Windows 95 не используют Unicode, а работают с кодовыми страницами. Однако в этой системе предусмотрена возможность динамического изменения наборов символов и раскладок клавиатуры, что позволяет создавать документы, содержащие одновременно символы из разных наборов. Буфер обмена Windows 95 способен хранить тексты в формате CF_UNICODETEXT. В составе Windows 95 и более поздних версий поставляется набор шрифтов Unicode, с которыми, в частности, могут работать программы Microsoft Office.

Выяснить, какие наборы символов присутствуют в том или ином шрифте Unicode, можно с помощью стандартной утилиты Character Map (таблица символов), включенной в

состав Windows NT. Выбрав в списке Subset строку Cyrillic, вы увидите таблицу с символами кириллицы, соответствующую кириллической области Unicode.

Использование Unicode значительно упрощает создание многоязычных документов, публикаций и программных приложений. Поэтому следует ожидать его широкого применения в электронных изданиях.

25

Логические основы ЭВМ

26