
раздел 3
.docx1)Оптимальное конструкторское решение—констр. решение, при котором достигается экстремальное (наилучшее) значение интересующего технико-экономического показателя (одного или нескольких).
2) Целевая функция. О том, достигнуто ли оптимальное решение судят по выражению:F(x1,…,xn) →ext , где ext минимум или максимум знач-я ф-и F в зав-ти от того, что явл-ся лучше; n-кол-во оптимизируемых параметров; x1,…,xn – оптим-мые параметры, знач-ями этих параметров констр-я воплощ-ся в жизнь.
3) Ее также называют критерием оптимальности, функцией качества, критериальной функцией и т.д.
4) Оптимизируемые параметры. Параметры конструкторско-технологического решения, от значений которых в значительной степени зависит целевая функ-ция, рассматриваются как оптимизируемые параметры.
5) Оптимизируемые параметры. Параметры конструкторско-технологического решения, от значений которых в значительной степени зависит целевая функ-ция, рассматриваются как оптимизируемые параметры.
6)
7) Выявляются технико-экономические показатели, важнейшие для данного вида РЭУ с позиций создания этого устройства и его использования по назначению(на этом этапе пользуются анализом и требованиями заказчика).
8) На остальные технико-экономические показатели Q j, из числа не включенных в целевую функцию F, накладываются ограничения вида (7.2) или (7.3). Причем необходимо уточнить, какой конкретно вид ограничения должен быть наложен на технико-экономический показатель Q j, j = 1, ...
Q j≤ Q jдоп (7.2), Q j≥ Q jдоп(7.3), где Q jдоп — допустимое значение j-го технико-экономического показателя, не вошедшего в состав целевой функции F.
9)Это когда слева иксы, справа игрики и выразить одно через другое нельзя
10) На этом же этапе необходимо выявить ограничения, накладываемые на опти-мизируемые параметры, исходя из их конструкторских и физических особенностей.
11) Задачи безусловной оптимизации –задачи, в которых не наклад-ся ограничения на оптимальные пар-ры или какие-то ТЭП, зависящие от оптимальных параметров.
12) Задачи условной оптимизации –задачи, в которых наклад-ся ограничения на оптимальные пар-ры или какие-то ТЭП, зависящие от оптимальных параметров.
13) большинство математических методов оптимизации предполагает минимизацию целевой функции F. Если в конкретной задаче необходимо искать максимум функции F, то условие поиска оптимума F(х1, ... , хп) → mах заменяют условием –F(х1, ..., хп) → min.
14) Метод главного критерия или принцип главного критерия, метод взвешивания ТЭП и метод взвешивания нормированных значений ТЭП.
15) Метод главного критерия или принцип главного критерия .Суть его состоит в том, что из т важнейших технико-экономических показателей выбирается один, наиболее важный (главный). Он используется в качестве целевой функции, т.е. F= Q1.
На
остальные технико-экономические
показатели Q2,…,Qm
накладываются
ограничения вида (7.2) или (7.3):
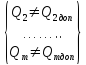 (7.6)
(7.6)
В выражениях (7.6) знак <> означает, что конкретный вид со-отношения уточняется с учетом физических особенностей техни-ко-экономического показателя и его лучшего значения для рас-сматриваемого вида РЭУ.
16) Этот принцип базируется на приведении показателей к относительным величинам (относительно априорно назначенного некоторого их уровня, исходя из функционирования и потребительских свойств РЭУ). Наиболее простым является подход, при котором целевая функция F формируется в виде выражения
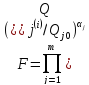 (7.7),
где
(7.7),
где
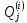 —
значение j-го
показателя в текущем (i-м)
варианте;
—
значение j-го
показателя в текущем (i-м)
варианте; —
экстремальное, но реально достижимое
значение j-го
показателя;
—
экстремальное, но реально достижимое
значение j-го
показателя;
αj— весовой коэффициент j-го показателя (0 < α < 1); т — число принятых во внимание показателей. Весовые коэффициенты αj назначаются, как правило, на основании экспертных оценок. Недостатком выражения (7.7) является, то, что экстремальные (лучшие) значения всех технико-экономических показателей, входящие в него, должны соответствовать либо минимуму, либо максимуму.
17) Указанного недостатка лишено выражение (недостаток написан в 16 вопросе)
F=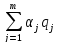 или F=
или F=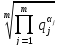
где qj — безразмерное нормированное значение j-го показателя.
Должно
вып-ся условие
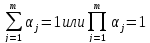
Значение qj могут быть определены, например, с использованием соотношения
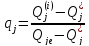 ,где
,где
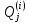 —
текущее (в i-м
варианте) значение j-го
показателя;
—
текущее (в i-м
варианте) значение j-го
показателя;
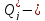 критическое
(допустимое) значение j-го
показателя;
критическое
(допустимое) значение j-го
показателя;
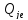 —
экстремальное,
но реально достижимое значение j-го
показателя.
—
экстремальное,
но реально достижимое значение j-го
показателя.
Достоинством выражений (7.8) является то, что показатели qj изменяются в диапазоне (0...1),причем лучшее (экстремальное) значение соответствует точке qj = 1. Поэтому при использовании в качестве целевой функции выражений (7.8) условием оптимальности решения является F→max.
18)Нормировка—процедура
переноса значений пар-ра в другую более
узкую обычно область и при этом параметр
теряет размерность. В инженерной практике
популярна нормировка при которой
значения параметров переносят в диапазон
(0…1), причем нормировку вып-т таким
образом, что т.1 соотв-т лучшему знач-ю
пар-ра, а т.0—предельно худшему. Для
вып-я нормировки используют выражение

(см. вопрос 17)
19) Метод безусловной оптимизации и метод условной оптимизации.
20)Косвенные
методы сводят решение задачи безусловной
оптимизации к решению системы нелинейных
уравнений, являющихся следствием
экстремума функции многих переменных.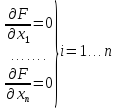
Эти условия образуют систему n нелинейных ур-ний, решая которые находят точки минимума.
21)-//-(тоже, что и в 20 вопросе )
22)Суть прямых методов сост-т в построении последовательности векторов Х[0], Х[1]… Х[q], таких, что F(Х[0])> F(Х[1])>…> F(Х[q])
Вектор
Х=
Переход (итерация) от точки X[k] к точке X[k+1], k=0,1,2…состоит из 2-х этапов:
1)Выбор напр-я движения из точки X[k]
2)Опред-е шага вдоль этого напр-я.
Методы
постр-я таких послед-й часто наз-т
методами спуска, т.к. осущ-ся переход от
больших знач-й ф-и F(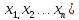 к меньшим.
к меньшим.
23)Матем-ки методы спуска в корд-ной форме опис-ся соотн-ми:
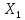 [k+1]=
[k+1]=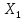 [k]+
[k]+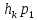 [k]
[k]
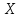 [k+1]=
[k+1]=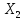 [k]+
[k]+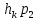 [k]
[k]
…………………..
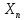 [k+1]=
[k+1]=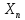 [k]+
[k]+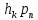 [k]
[k]
Где
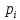 [k]—вел-на,
опред-щая напр-е спуска по i-й координате,
соотвествует k-й итерации(приближения);
[k]—вел-на,
опред-щая напр-е спуска по i-й координате,
соотвествует k-й итерации(приближения);
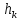 -шаг
поиска оптимума.
-шаг
поиска оптимума.
24)Условие прекращения итеративного процесса:
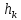 ≤
≤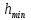 или
|F(X[k])-
F(X[k-1])|≤ˠ,
где
или
|F(X[k])-
F(X[k-1])|≤ˠ,
где
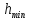 и ˠ, величины
, определяющие прекращение процесса
движения к опт-му.
и ˠ, величины
, определяющие прекращение процесса
движения к опт-му.
25)Разл-е
методы спуска отл-ся друг от друга
способами выбора двух пар-ров –напр-я
спуска
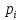 [k]
и длины шага
[k]
и длины шага
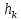 вдоль этого напр-я.
вдоль этого напр-я.
26) Детерминированными наз-т методы поиска т. Min, если оба пар-ра (напр-е спуска и значение шага) при переходе от X[k] к X[k+1] выбираются однозначно по имеющейся в точке X[k] инф-ции.
27)В
методах случ-го поиска при переходе от
X[k]
к X[k+1]
исп-т случ-й мех-зм выбора хотя бы одной
из величин
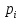 [k]
и
[k]
и
 .
.
28)В
методах нулевого порядка на каждой
итерации испт-т лишь значения минимизируемой
нулевой функции F(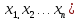 .
Эти методы весьма актуальны для инж-х
приложений ввиду того ,что в технике во
многих случаях целевая функция F в явной
аналитической форме не может быть
представлена.
.
Эти методы весьма актуальны для инж-х
приложений ввиду того ,что в технике во
многих случаях целевая функция F в явной
аналитической форме не может быть
представлена.
29) В методах первого порядка на каждой итерации польз-ся как значениями самой целевой функции, так и ее первыми производными . Произв-е исп-ся для выбора направления движения к оптимуму.
30) Под градиентными методами решения задач оптимизации понимают методы первого порядка, т.е. см. вопр.29.
31)
В методах второго порядка польз-ся
доп-но вторыми производными ф-и F(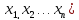 .
.
32) Математическое программирование — раздел математики, занимающийся разработкой методов решения задач оптимизации.
33) Линейное рассматривает решение задач оптимизации в случае, когда целевая функция F и функции Qj , задающие ограничения, имеют линейный характер. Нелинейное рассматривает решение задач оптимизации в случае нелинейного вида хотя бы одной из функций F и Qj , j=1, 2, ...
34)С помощью методов нелин-го матем-го программ-я можно решить любую задачу оптим-и—как при нелинейном, так и при линейном виде указ-х ф-й.
35)Если целевая функция F и ограничения задачи представляют собой линейные функции независимых переменных, то задачу оптимизации называют задачей линейного математического программирования. Для ее решения пригодны методы лин. прогр-я , кот. могут оперировать как с непрерывными, так и с целочисленными значениями оптим-мых пар-ров.В посл-м случае исп-мые методы называют методами целочисленного лин-го прогр-я.(В методах лин. прогр-я рассматривается решение задач минимизации или максимизации лин-х ф-й на множествах, задаваемых сист-ми лин. равенств и неравенств. Причем число равенств и неравенств может быть как меньше, так и больше числа опт-мых парам-в, т.е. аргументов ф-и F)
36) При линейном виде целевой функции F на практике широко используют так называемый симплексный метод.
38) Методы спуска при переходе от k-й итерации к (k+1) итерации в координатной
форме описываются соотн-ми:
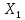 [k+1]=
[k+1]=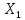 [k]+
[k]+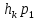 [k]
[k]
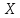 [k+1]=
[k+1]=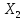 [k]+
[k]+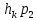 [k]
[k]
…………………..
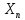 [k+1]=
[k+1]=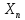 [k]+
[k]+ [k]
[k]
Где
 [k]—вел-на,
опред-щая напр-е спуска по i-й координате,
соотвествует k-й итерации(приближения);
[k]—вел-на,
опред-щая напр-е спуска по i-й координате,
соотвествует k-й итерации(приближения);
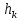 -шаг
поиска оптимума.
-шаг
поиска оптимума.
В большинстве методах спуска точки X[K] выбирают так, чтобы для них выполнялись все ограничения задачи, т.е. мы должны находиться в области решений допустимых задачи.
39)Каждая
точка в n-мерном простр-ве перемен-х
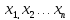 ,
в кот-й вып-ся огр-я задачи , называется
допустимой точкой задачи. Множество
всех точек наз-ся доп-й областью.
,
в кот-й вып-ся огр-я задачи , называется
допустимой точкой задачи. Множество
всех точек наз-ся доп-й областью.
40)Методы штрафных функций относятся к группе непрямых методов реш-я задач нелин-го прогр-я. Эти методы преобразуют задачу с огр-ми в последовательность задач безусловной оптимизации нек-х вспомог-х функций. Последние получают путем модификации целевой ф-и с помощью ф-й огранич-й таким образом, чтобы сами ограничения в явном виде в задаче оптимизации не фигурировали. Это обеспечивает возм-ть применения методов безусловной оптимизации.
41) В общем случае вспомогательная функция имеет вид:
f(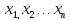 ,λ)=
F(
,λ)=
F(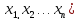 +Ф(
+Ф(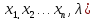 ,
где Ф(
,
где Ф(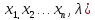 —штрафная
ф-я.
—штрафная
ф-я.
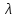 -параметр
(
-параметр
(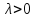 )
)
42) Выбор этого метода, прежде всего, зависит от наличия либо отсутствия ограничений, накладываемых на технико-экономические показатели Qj, а также на сами оптимизируемые параметры х1, ..., хп.
Вторым важнейшим фактором, определяющим выбор метода решения задачи оптимизации, является линейный или нелинейный вид уравнений, задающих математические выражения для функ-ций F и Qj. Если хотя бы одна из функций F или Qj, имеет нелинейный вид, то это потребует выбора одного из методов, ориентированных на решение задач нелинейного математического программирования.
Третьим важнейшим фактором, определяющим выбор математического метода решения задач оптимизации, является количество оптимизируемых параметров, участвующих в задаче оптимизации.
Четвертый фактор — наличие или отсутствие ЭВМ большой производительности, что определяет возможность использования численных методов оптимизации.
43) Основные достоинства оптимизации методами случайного поиска: 1)простота программной реализации, 2)отпадает необходимость иметь целевую функцию в виде явного аналит-го выраж-я (метод не предусм-т взятие производных), 3)метод эфф-н при большом числе оптим-мых пар-ров, 4) малое время решения задачи на ЭВМ.
44) Наиболее простой алгоритм случайного поиска для случая минимизации целевой функции F задается итеративным выражением
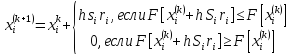
где k — номер итерации (приближения к оптимуму);
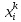 —
значение
i-го
оптимизируемого параметра в k-й
интеграции;
—
значение
i-го
оптимизируемого параметра в k-й
интеграции;
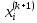 —
значение
i-го
оптимизируемого параметра в k+1
интеграции;
—
значение
i-го
оптимизируемого параметра в k+1
интеграции;
h — шаг поиска оптимума
ri — случайное число с равномерным законом распределения в диапазоне (–1... + 1), используемое для определения значения и направления смещения (рабочего шага) i-го оптимизируемого параметра;
Si — приращение, установленное для i-го оптимизируемого параметра, называемое также шкальным коэффициентом.
Шкальные коэффициенты Si определяют по выражению
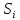 =
=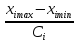
где Сi — константы, в общем случае различные по значению для каждого оптимизируемого параметра (Сi = 5...30);
 ,—
максимальное и минимальное ограничения,
накладываемые на i-й
оптимизируемый параметр.
,—
максимальное и минимальное ограничения,
накладываемые на i-й
оптимизируемый параметр.
45) Чтобы решить задачу оптимизации с помощью описанного алгоритма, начальные значения оптимизируемых параметров в итерации с номером k = 0 не должны нарушать ограничения вида (7.13), (7.15) или (7.16)
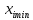 ≤
≤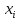 ≤
≤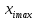 (7.13)
(7.13)
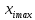 ,
,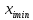 —
максимальное и минимальное ограничения,
накладываемые на i-й
оптимизируемый параметр.
—
максимальное и минимальное ограничения,
накладываемые на i-й
оптимизируемый параметр.
В реальных ситуациях на технико-экономических показатели, не вошедшие в целевую функцию F, могут накладываться ограничения вида
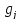 (
(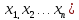 ≤
≤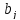 j=1,…l
(7.15)
или
j=1,…l
(7.15)
или
 (
(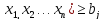 j=1,…l
(7.16)
j=1,…l
(7.16)
где gj — технико-экономический показатель, являющийся некоторой функцией оптимизируемых параметров; x1,…,xn;
bj — допустимое значение j-го показателя, представляющее собой константу, не зависящую от параметров x1, …, xn;
l — количество показателей, на которые наложены ограничения.
46)Нет, нельзя потому что целевая функция по логике вещей непрерывная функция и у неё куча вариантов решений, путем перебора вариантов решений можно сколько угодно долго искать решение.
47)Метод динамического программирования предназначен для решения задач условной оптимизации.
48) Этот метод отличается от простого перебора тем, что промежуточные заведомо неудачные решения отбрасываются еще на начальных этапах движения к оптимуму.
49) Динамическое программирование — шаговый процесс.
Рассматриваемое устройство или процесс разбиваются на составные части (компоненты), и на каждом шаге принимаются во внимание лишь две компоненты.
На первом шаге на основе анализа двух взятых компонент выделяются варианты (ситуации), которые предположительно еще могут привести к получению оптимального решения в целом. Эти выделенные варианты на втором шаге уже рассматриваются как одна новая компонента, а в качестве второй к ним добавляется следующая составная часть устройства или процесса. Так как новых компонент после первого шага может быть несколько, то на втором, а далее и на последующих шагах число рассматриваемых пар компонент также растет.
50)
Недостатки:
во-первых, при
большом количестве этапов решение
полученной системы довольно громоздко;
во-вторых, с его помощью можно найти
критические точки только внутри области,
так как метод не позволяет исследовать
граничные точки; в-третьих, метод вообще
неприменим, если
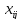 дискретные величины.
дискретные величины.
